1 - 2 - 3 klasse
Lær VGS matten fra A til Å
med de beste metodene
Enkelt å
holde fokus
Forstå det
vanskelige
Få god
oversikt
Øv på
riktig tema
Få hjelp når
du stopper opp
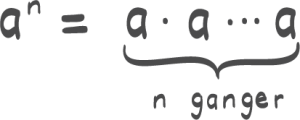
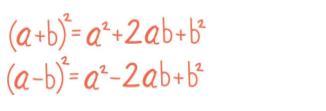
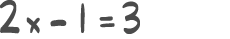
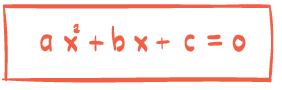
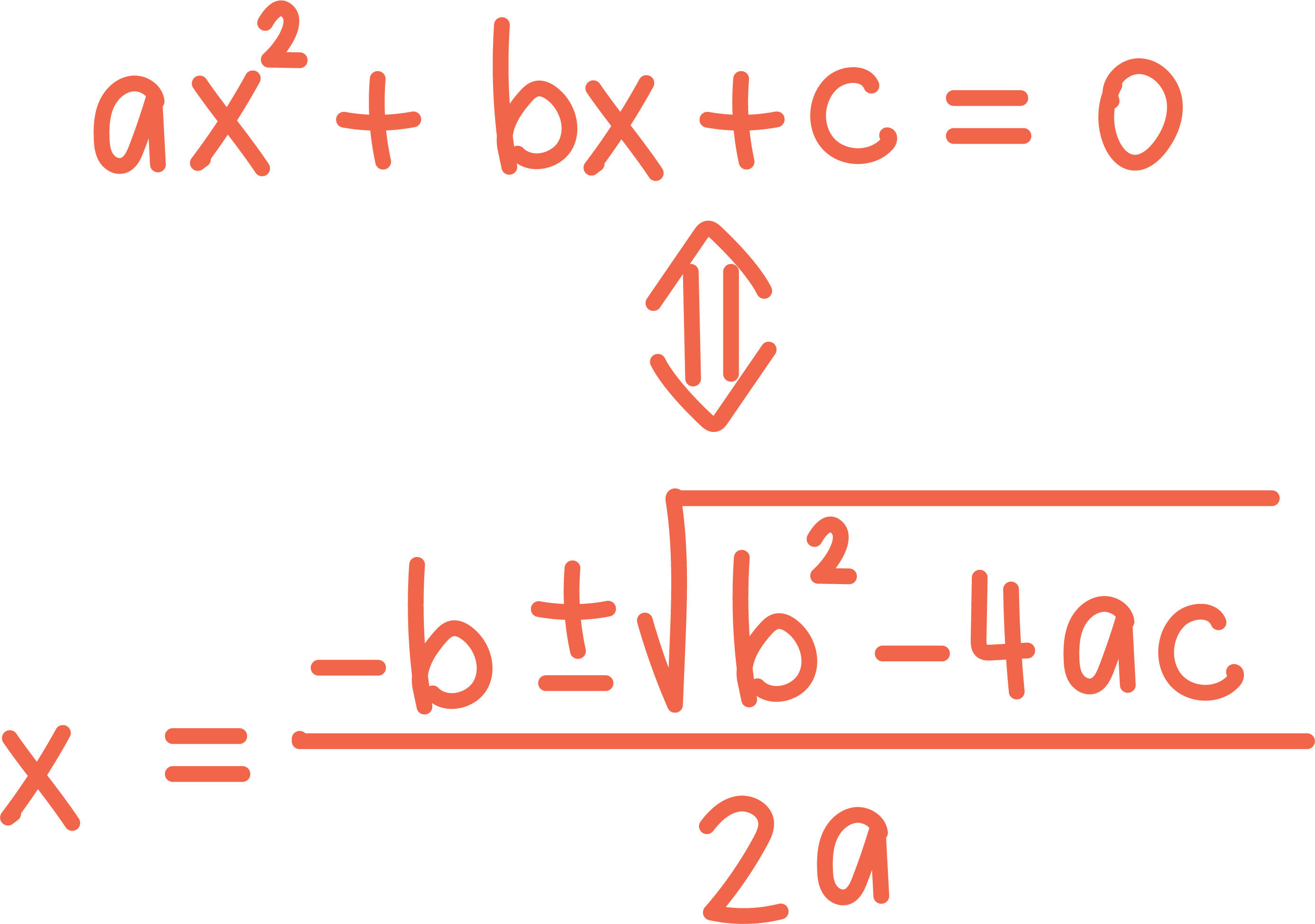
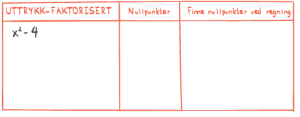
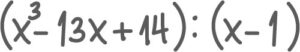
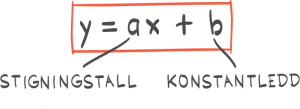
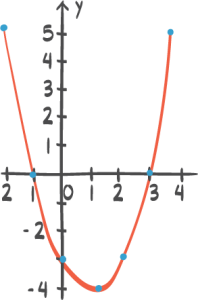
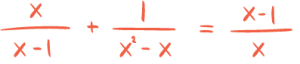
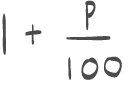
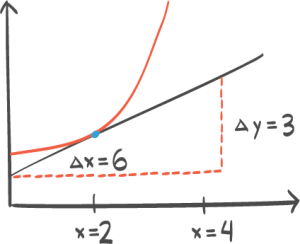
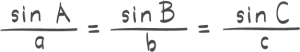
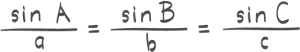
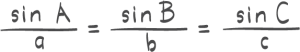
Oppgave 1 (2 poeng)
Løs likningssettet
Oppgave 2 (1 poeng)
Løs likningen
Oppgave 3 (2 poeng)
Regn ut og skriv svaret på standardform
Oppgave 4 (1 poeng)
Vis at
Oppgave 5 (2 poeng)
Regn ut og skriv svaret så enkelt som mulig
Oppgave 6 (3 poeng)
a) Vis atb) Løs likningen
Oppgave 7 (2 poeng)
Løs ulikheten
Oppgave 8 (3 poeng)
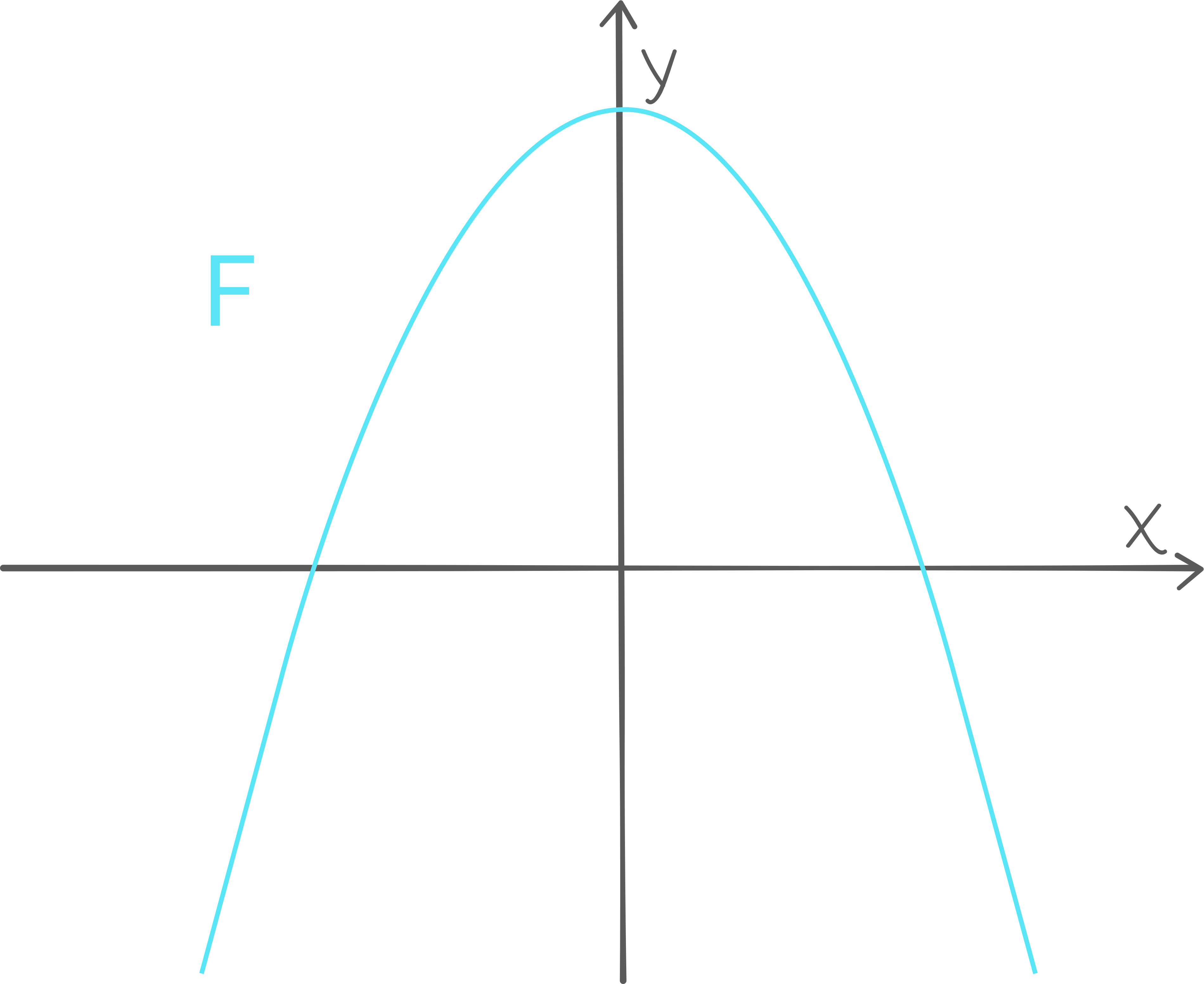
Funksjonener gitt vedFor hvilke verdier av har grafen til
- ingen skjæringspunkter med x-aksen
- ett skjæringspunkt med x-aksen
- to skjæringspunkter med x-aksen
Oppgave 9 (3 poeng)
a) Vis atb) Skriv så enkelt som mulig
Oppgave 10 (4 poeng)
En funksjon er gitt ved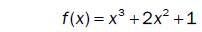
a) Bestem den gjennomsnittlige vekstfarten til i intervallet .
b) Bestem likningen for tangenten til grafen til i punktet .
Oppgave 11 (3 poeng)
- Terningene viser samme antall øyne.
- Summen av antall øyne er 5 eller mindre.
Oppgave 12 (6 poeng)
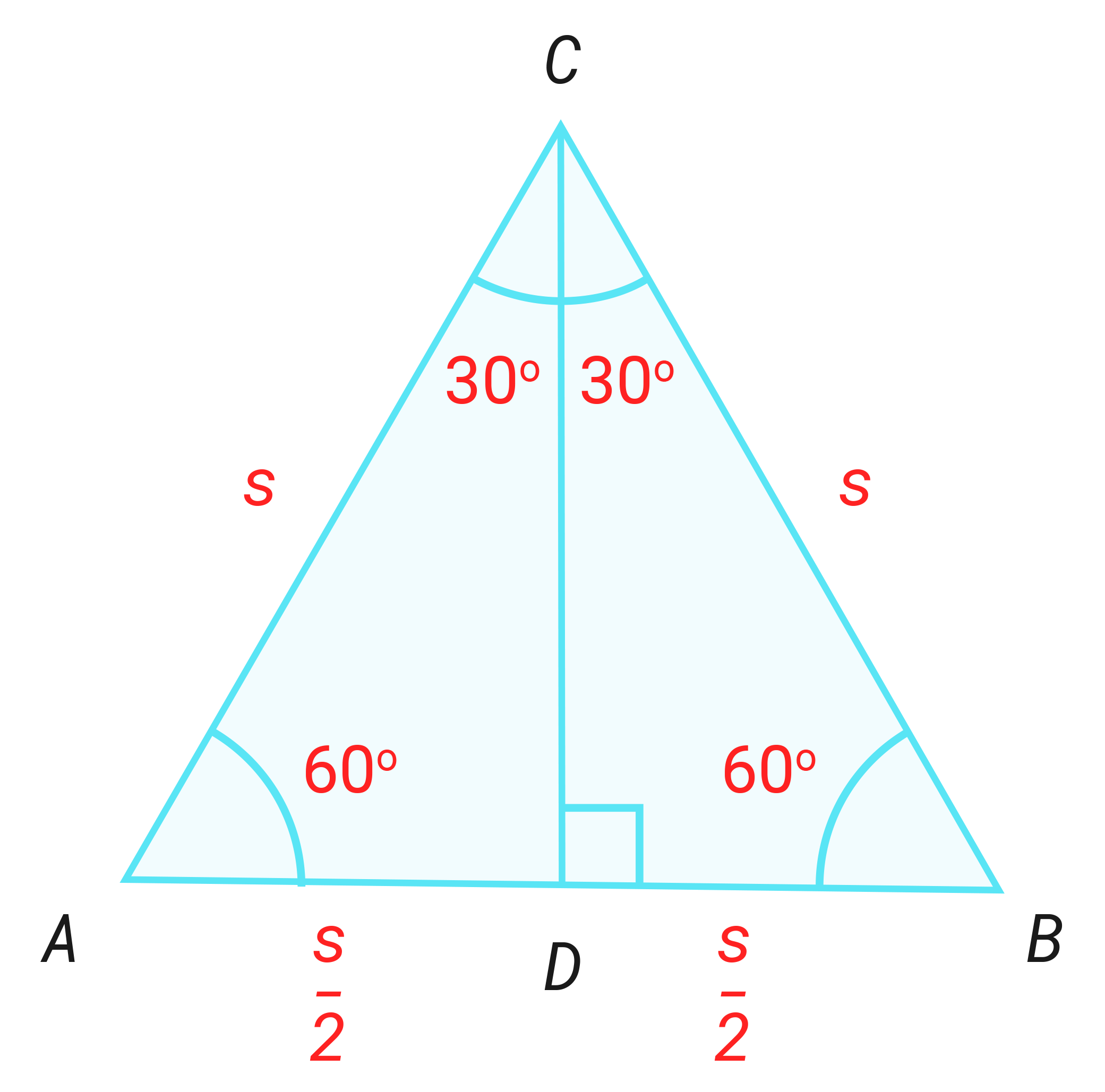
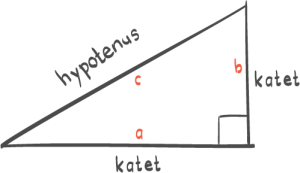
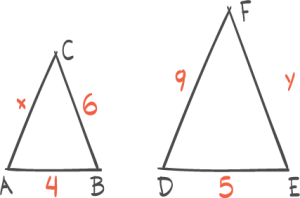
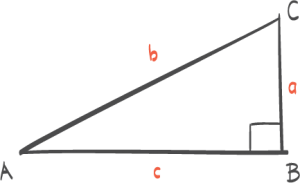
I en likesidet trekant er alle sidene like lange og alle vinklene 60° . Høyden på en av sidene halverer denne siden.
Høyden deler den likesidete trekanten i to likestore rettvinklete trekanter.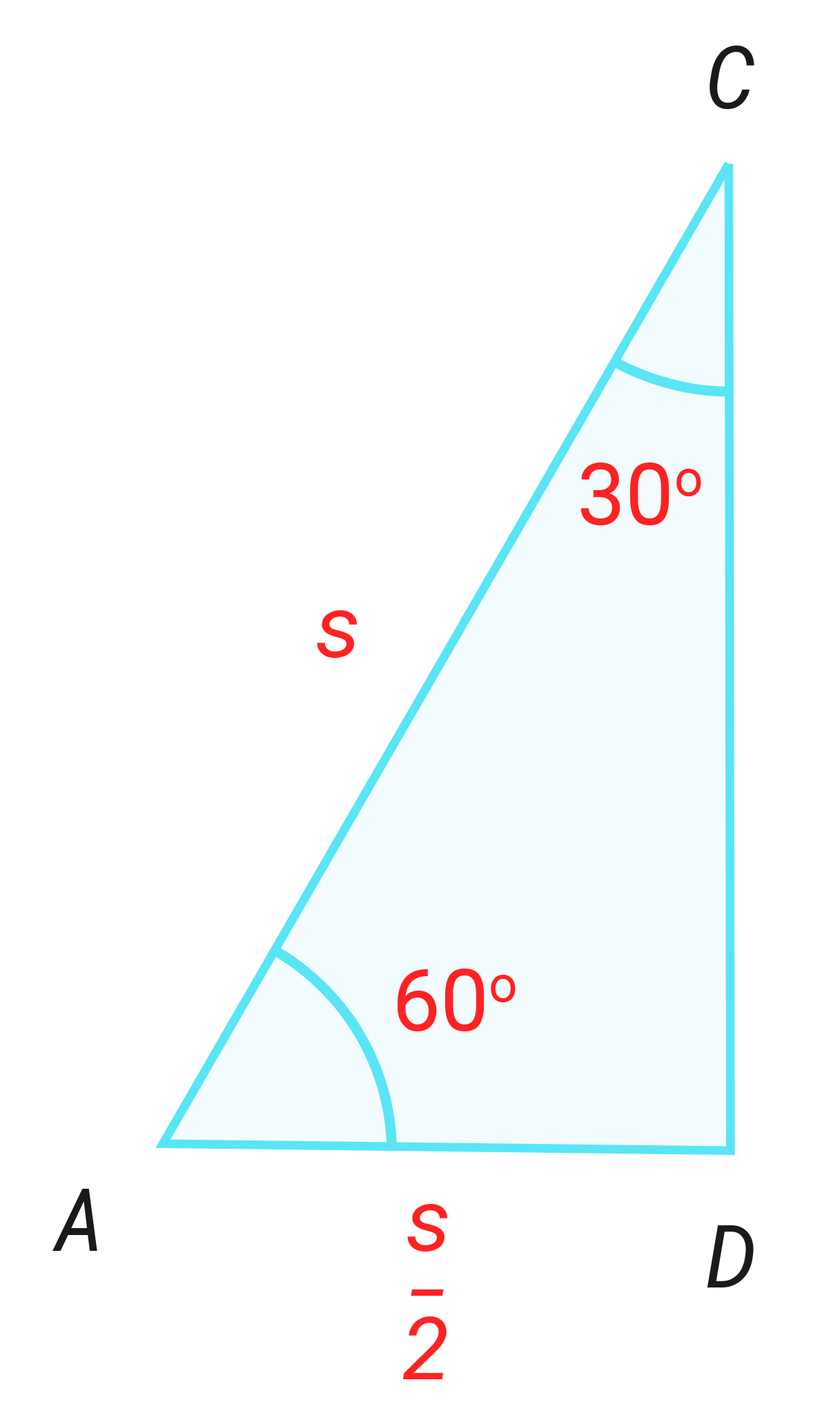
I denne rettvinklete trekanten er vinklene 30° , 60° og 90° . I tillegg er hypotenusen dobbelt så lang som den minste kateten.
Denne sammenhengen kalles 30° , 60° og 90° - setningen. Ovenfor ser du to avsnitt fra en lærebok for 10. klasse. a) Vis at b) Bruk til å vise at .
Oppgave 13 (4 poeng)
Fire andregradsfunksjoner p , q , r og s er gitt ved
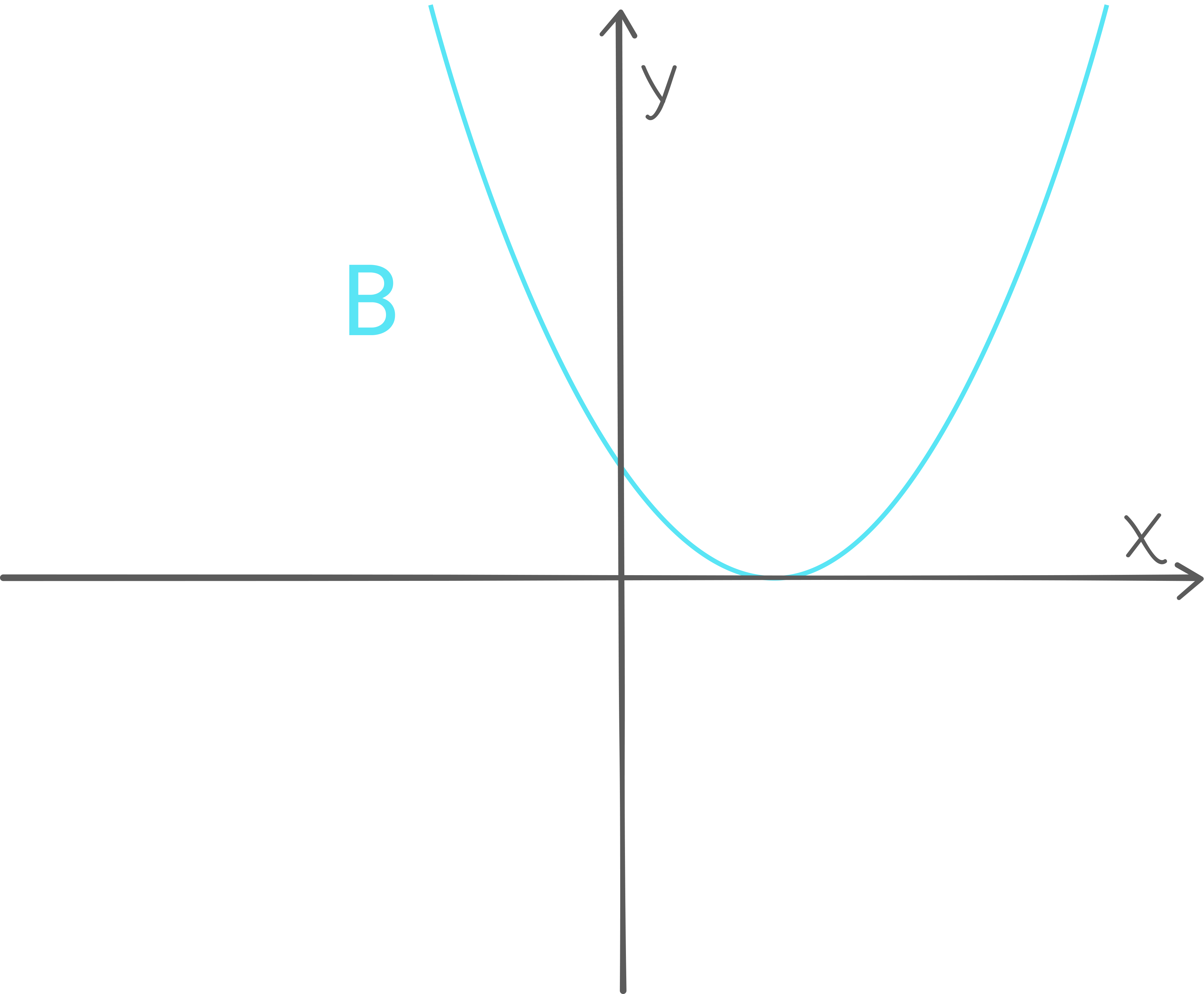
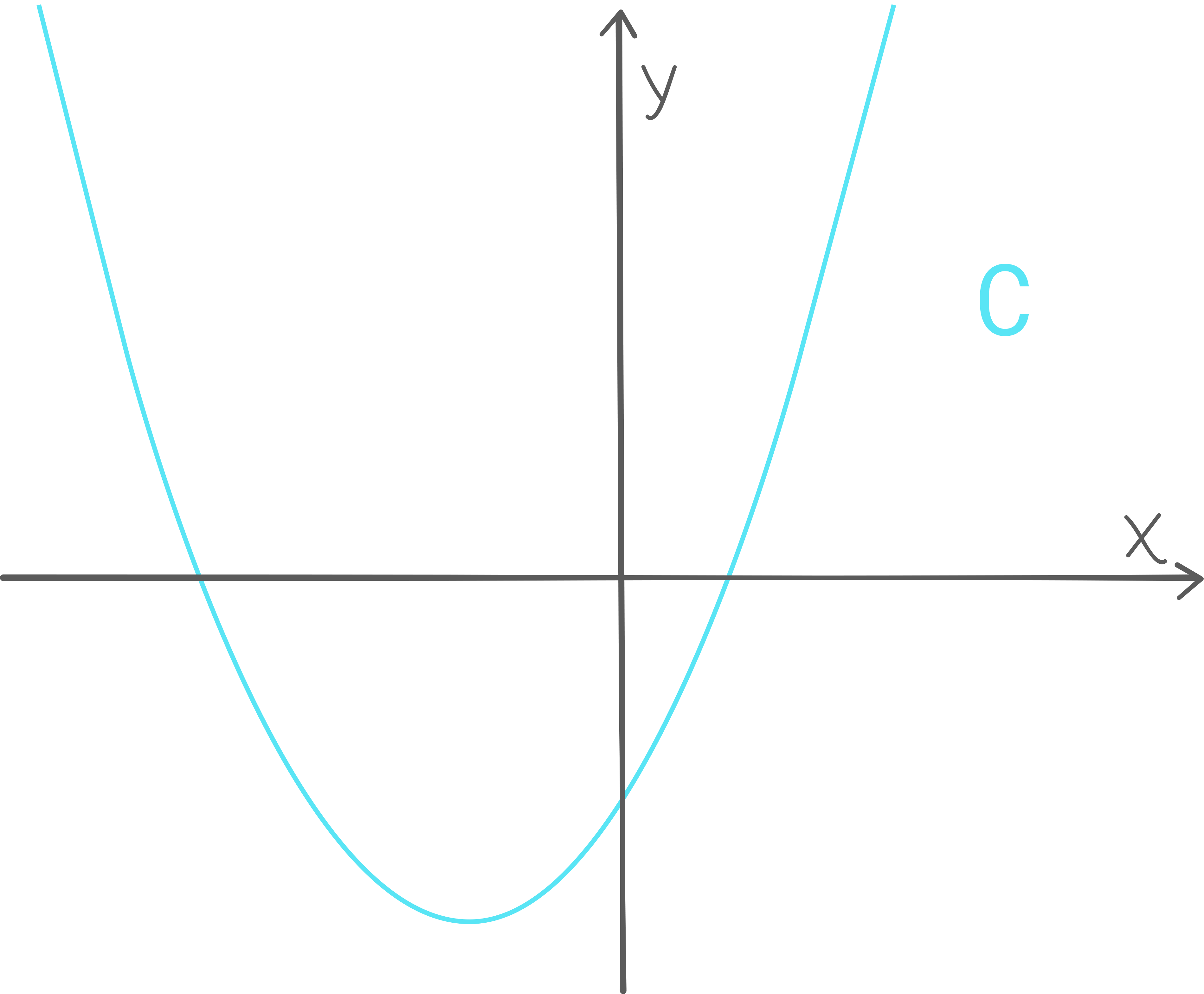
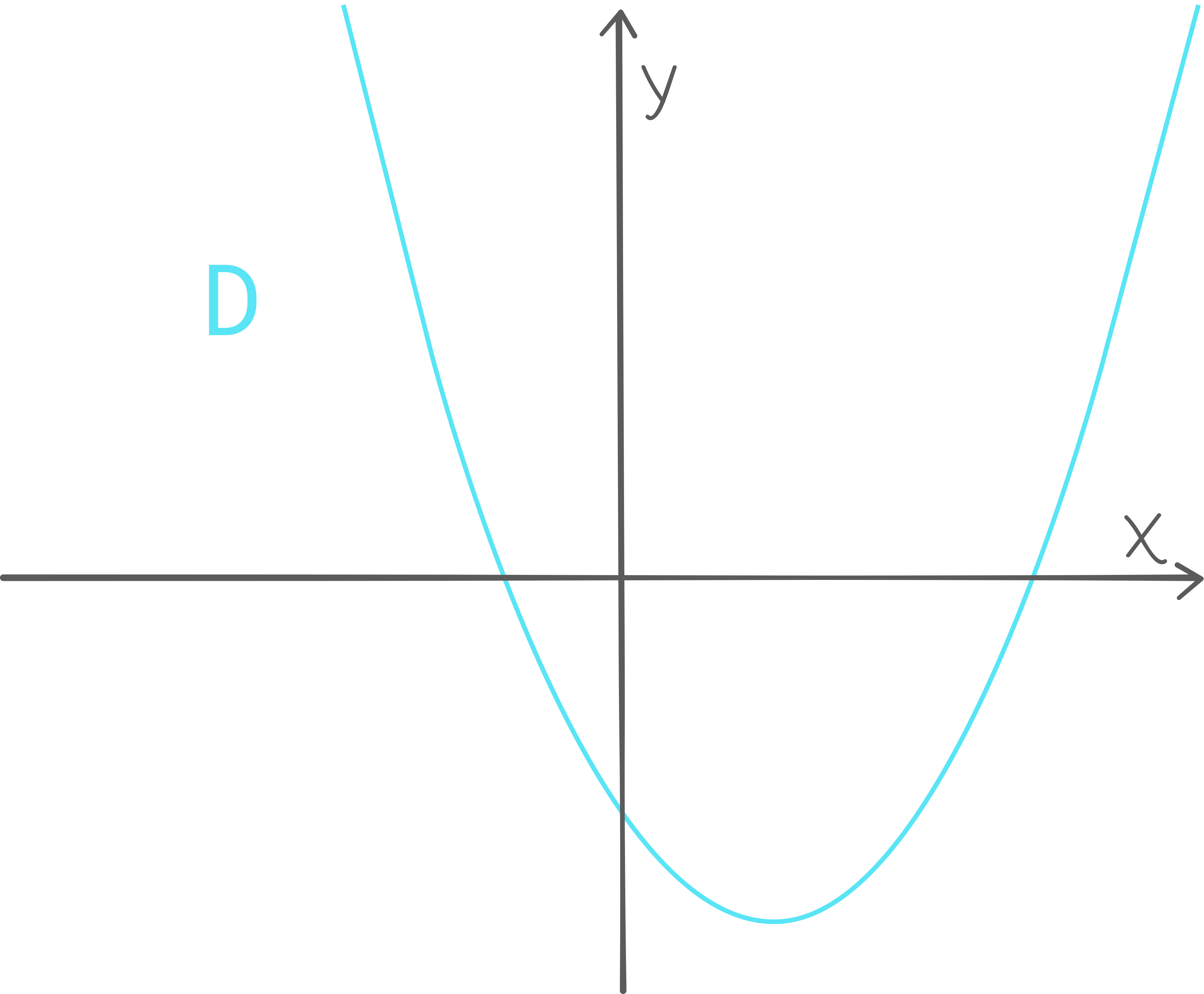
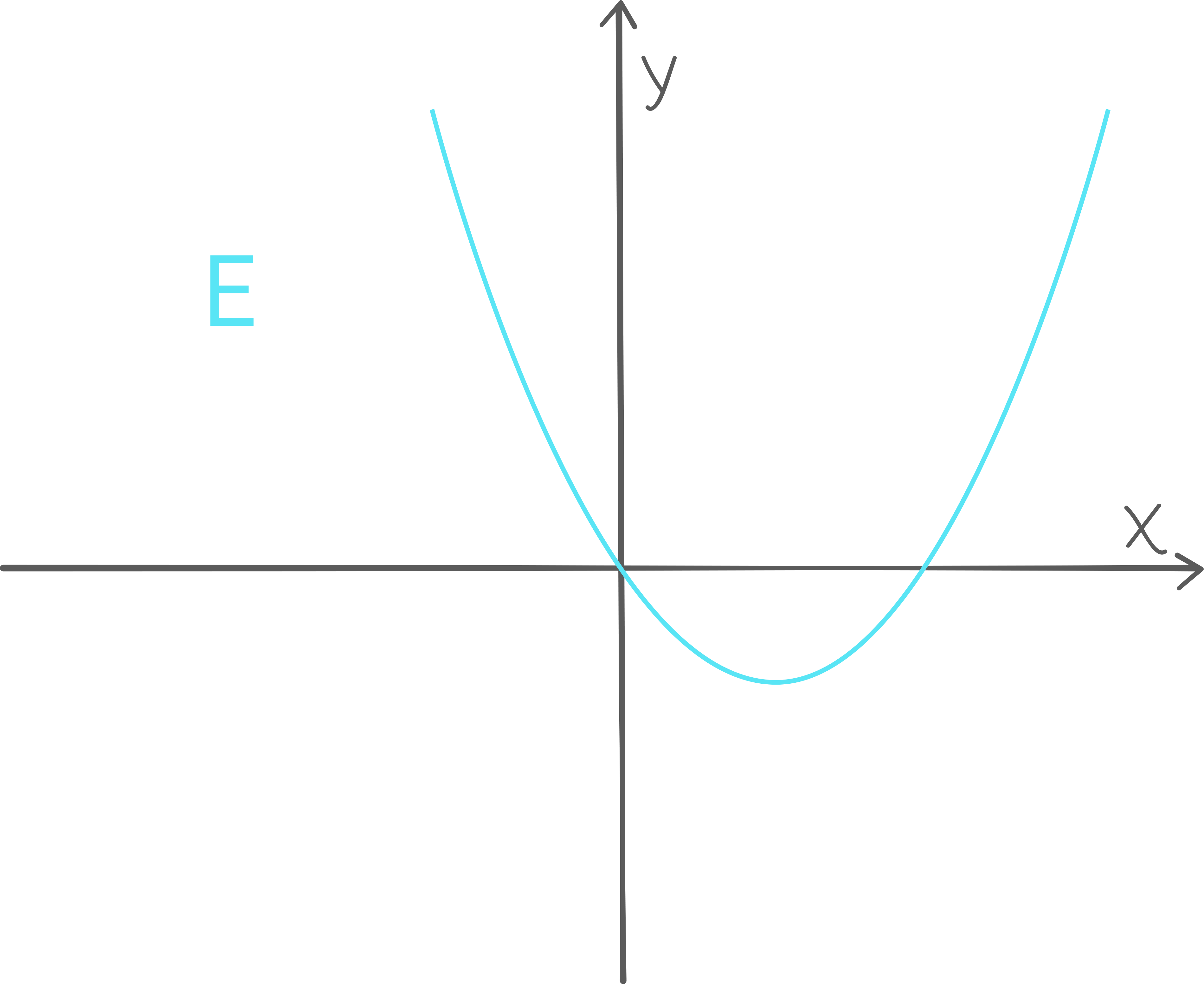
Oppgave 1 (6 poeng)
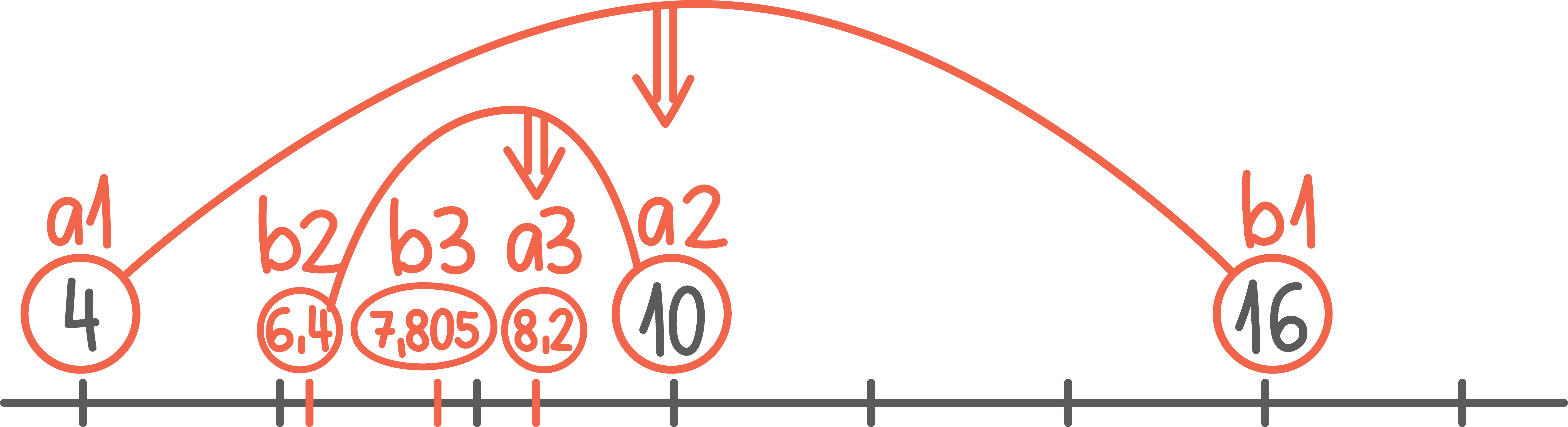
a) Legg opplysningene i tabellen ovenfor inn som punkter i et koordinatsystem der x-aksen viser antall år etter 1970 og y-aksen viser pris (kroner).
Funksjonen f er gitt vedb) Tegn grafen til i samme koordinatsystem som du brukte i oppgave a).
I resten av denne oppgaven skal du bruke funksjonen som en modell som viser prisen kroner for en kroneis år etter 1970.c) Når var prisen for en kroneis 16 kroner, ifølge modellen?
d) Hvor mye har prisen for en kroneis i gjennomsnitt steget med per år fra 1975 til 2015?
Oppgave 2 (4 poeng)
Ved en videregående skole er det 640 elever. I en undersøkelse ble elevene spurt om når de legger seg kvelden før en skoledag.- av elevene svarte at de legger seg før klokka 23.
- av elevene som legger seg før klokka 23, har et karaktersnitt over fire
- av elevene som legger seg etter klokka 23, har et karaktersnitt over fire
a) Lag en krysstabell som illustrerer opplysningene som er gitt ovenfor.
Tenk deg at vi trekker ut en elev ved skolen tilfeldig.b) Bestem sannsynligheten for at eleven har et karaktersnitt over fire.
Tenk deg at den eleven vi trakk i oppgave b), har et karaktersnitt over fire.c) Bestem sannsynligheten for at denne eleven legger seg før klokka 23 kvelden før en skoledag.
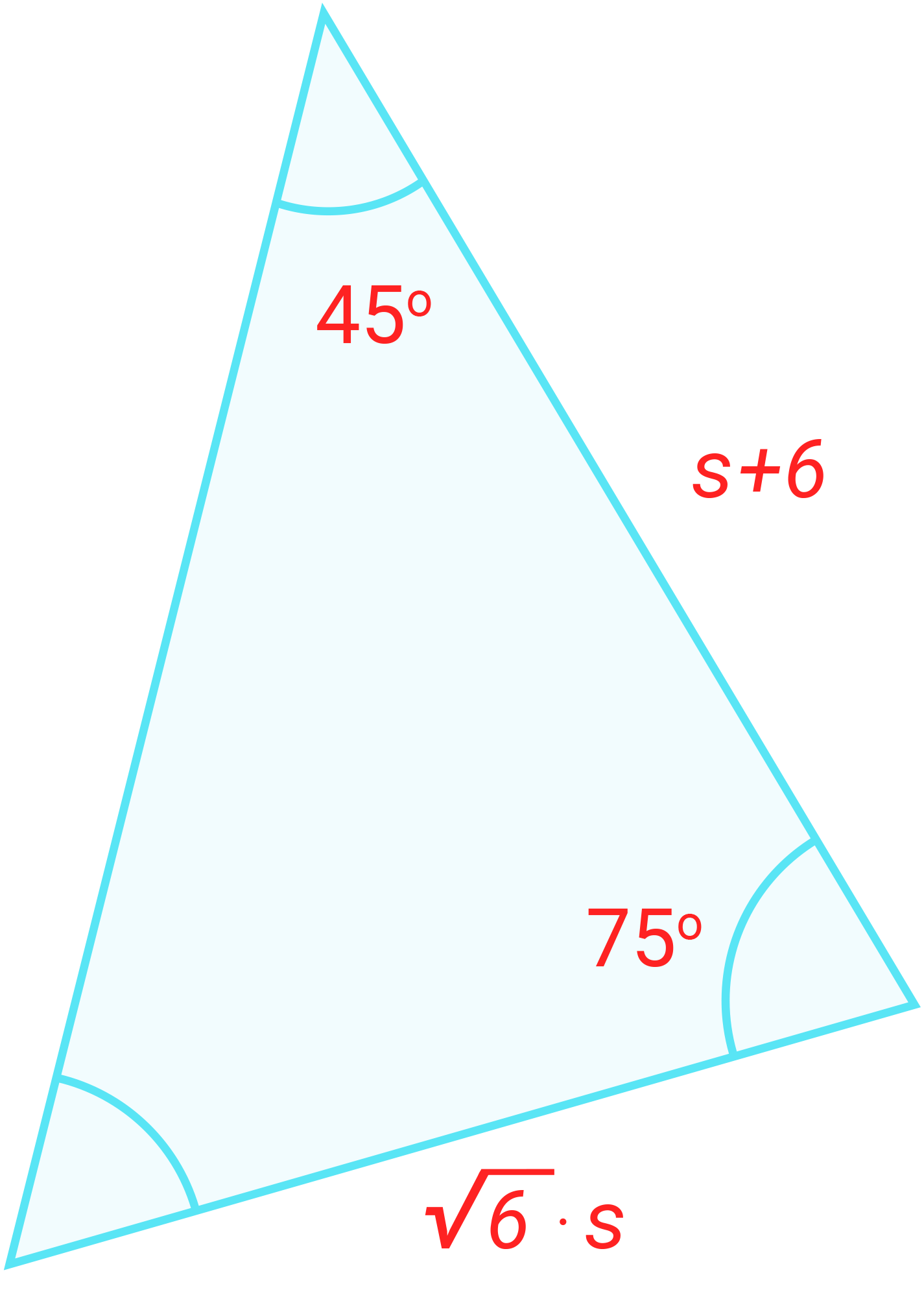
Oppgave 3 (2 poeng)
Oppgave 4 (6 poeng)
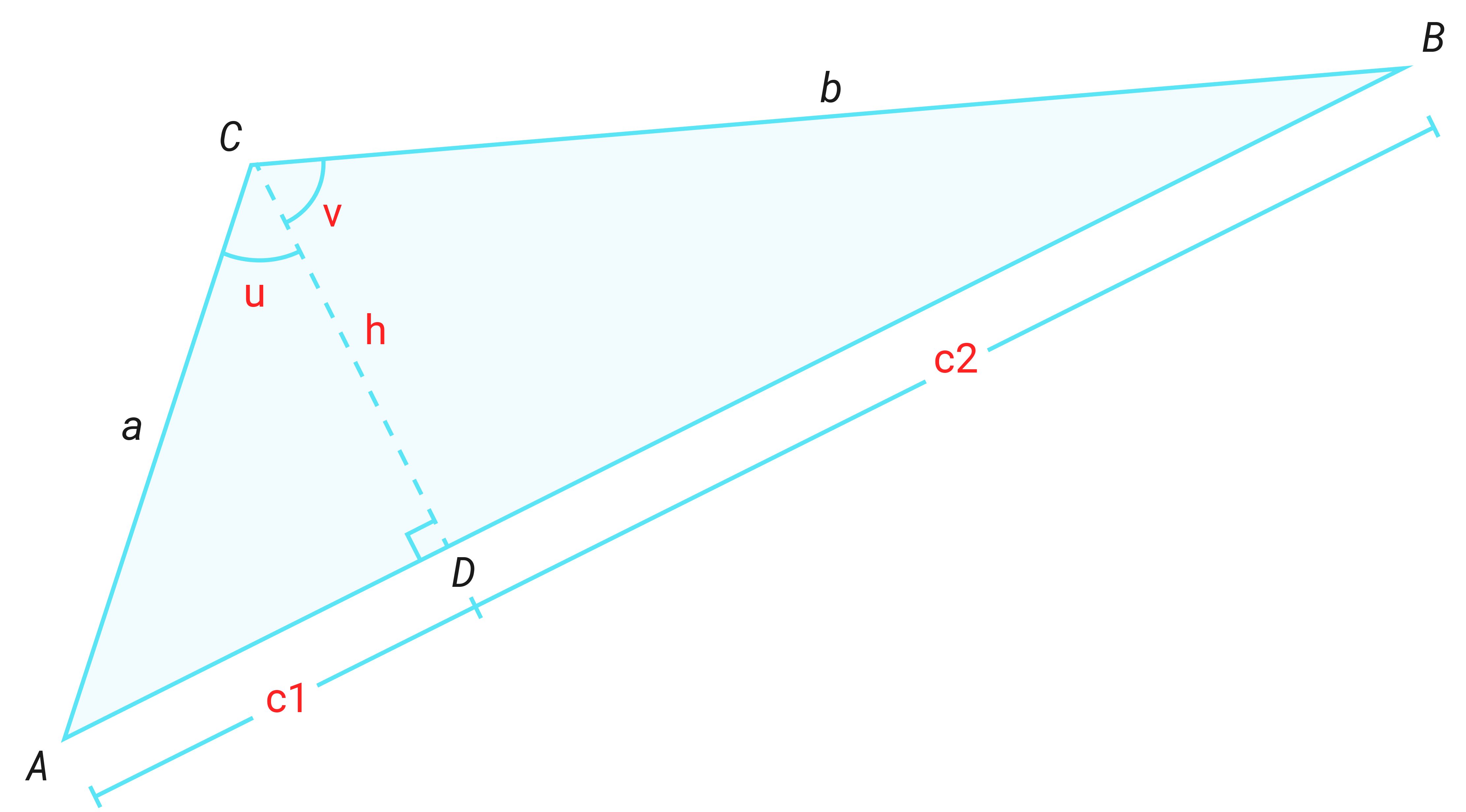
- 1)
- 2)
a) Vis at Maria har rett
For å bestemme arealet av vil Maria regne slik:b) Bruk blant annet resultatet fra oppgave a), og vis at dette uttrykket for arealet kan skrives som
Mats bruker arealsetningen og får at arealet av trekanten også kan skrives slik:c) Bruk dette uttrykket og uttrykket du har for arealet fra oppgave b), til å vise at
Oppgave 5 (6 poeng)
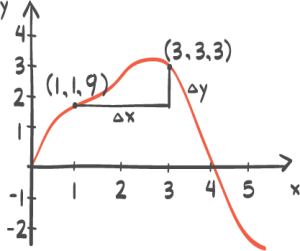
En funksjon f er gitt veda) Vis at tangeten til grafen til i punktet er parallell med linjen som går gjennom punktet og .
Nedenfor ser du grafen til en funksjon gitt ved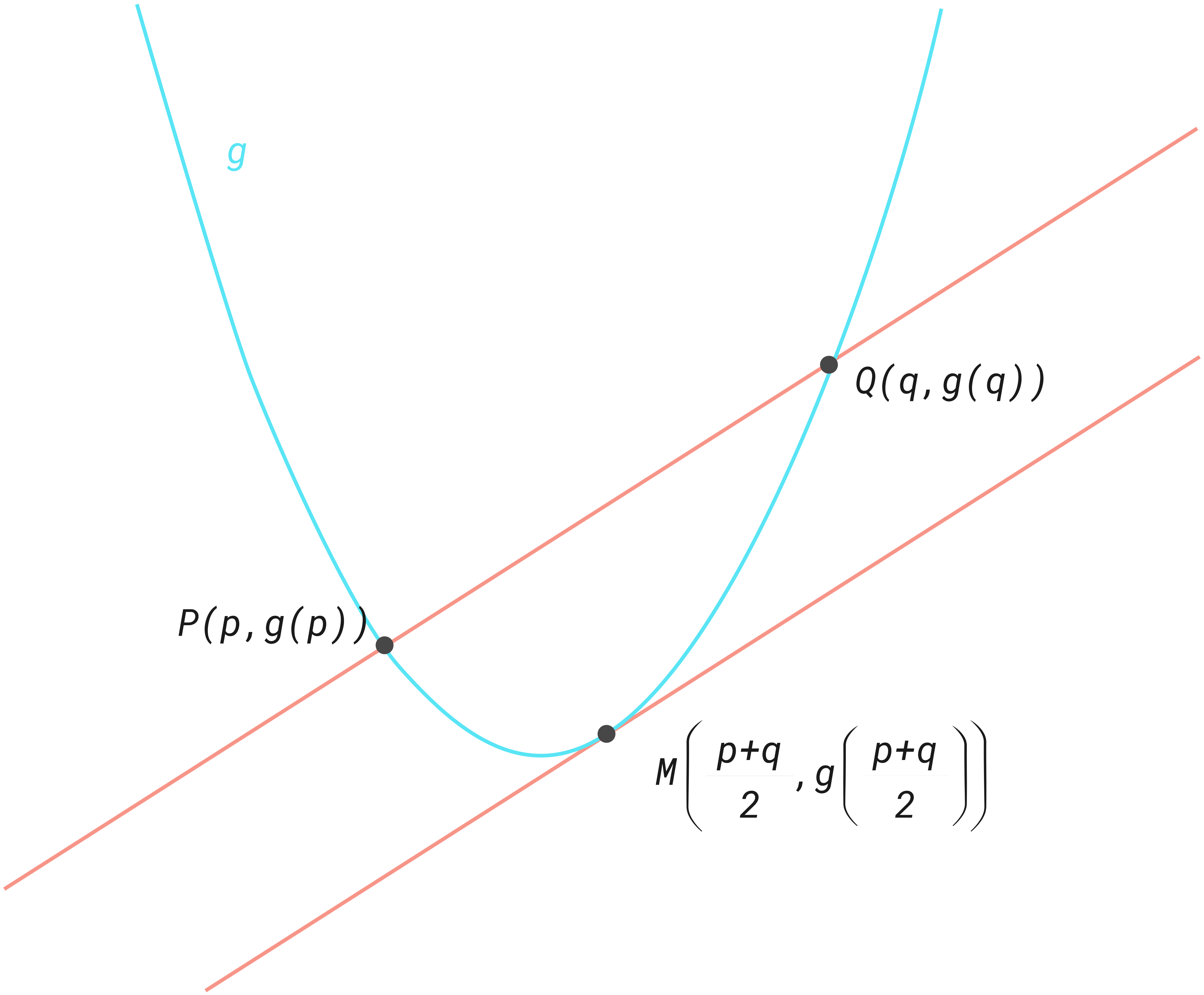
b) Bruk CAS til å bestemme stigningstallet til tangenten til grafen til g i punktet
c) Vis at linjen gjennom punktene P(p,g(p)) og Q(q,g(q)) er parallell med tangenten i oppgave b).
Prøvesmak våre videoer
Mattevideo tilbyr fullstendig dekning av kursene 1P, 1PY, 1T, 2P, S1, R1, S2 og R2 innenfor videregående skole. Under har vi lagt ut noen smakebiter fra disse kursene, så du kan sjekke ut noe av det vi har å by på, før du bestemmer deg for å bli abonnent.1P - Polynomfunksjoner1PY - Prosentregning1T - Funksjonsbegrepet2P - Første gradS1 - LikningssettR1 - Å finn den deriverte ved å bruke derivasjonsreglerS2 - Aritmetiske og geometriske rekkerR2 - Sinusfunksjoner og cosinusfunksjoner
Lær å jobbe smarterepå 5 minutter
Det finnes mange ulike studieteknikker, utfordringen er ofte å finne de som fungerer best for deg. I oversikten under finner du enkelt de beste teknikkene.
Alle våre studietips er laget av vår superelev - med 6 i snitt fra vgs. Ingen av artiklene tar mer enn 5 minutter å lese - slik at du kan starte læringen så fort som mulig.
Hva skjer i hjernen når du lærer?
Du møter noe nytt for første gang
Du kobler den nye tingen med kunnskap du har fra før
Du repeter og styrker sammenhengene
Du bruker kunnskapen
Vanlige utfordringer - og hvordan løse dem
Teknikkene som gjør deg til en superelev
La oss ringe deg, så finner vi en god løsning.
I denne videoen skal vi bruke potensregning, sånn som vi har lært før, til å se på [..].
klikk her for 10 sekunders quiz
Tierpotenser og standardform.
Her har vi grunndefinisjonene på potenser. Når vi har en positiv eksponent, så er en potens bare at et tall ganger med seg selv like mange ganger som eksponenten sier. Hvis vi har et tall opphøyd i nullte, så er det alltid lik én. Og hvis vi har et tall opphøyd i minus noe, så er det én delt på det samme med positiv eksponent.
Tierpotenser. En tierpotens er bare en potens med ti som grunntall. Så her ser vi forskjellige tierpotenser: ti i tredje, ti i nullte, ti i minus tredje, ti i sjette.
I hvert tilfelle kan vi bare bruke definisjonen og se hva vi får. Ti opphøyd i tredje, det må da bli ti ganger ti ganger ti, og det er tusen.
Ti opphøyd i sjette blir litt på samme måte.
Da blir det seks ganger.
Og for hver tier så får vi en null i svaret, så dette her blir en million. Skal vi se: en, to, tre, fire, fem, seks, det var riktig antall, og da blir det seks nuller i svaret også.
Legg merke til at på ti i tredje så var det tre nuller. Så det er et samsvar mellom antall nuller og eksponenten.
Ti i nullte. Alle tall i nullte er lik én.
Ti opphøyd i minus tre. Det vil være én delt på ti opphøyd i tredje.
Og det er én delt på ti ganger ti ganger ti, men nå har vi jo funnet ut at det er tusen allerede.
Så da blir det en tusendel, og det kan vi også skrive som desimaltallet null komma null null én. Og da ser vi også at faktisk, når vi skriver det som ti i minus tredje, så ser vi for det første at det er et veldig lite tall.
Og for det andre ser vi at det er tre nuller inkludert den første.
En, to, tre nuller, og så kommer det én og.
Tre nuller, og det var ti i minus tredje.
[..] Da kan vi også gå motsatt vei og gjøre et vanlig tall, normalt tall, den vanlige tall, om til tierpotenser. Ti tusen, det har fire nuller, og da blir det ti opphøyd i fjerde.
Null komma null null én. Det har også fire nuller.
Men det er jo et lite tall, så da blir det ti opphøyd i minus fjerde.
Litt av grunnen til at vi bruker tierpotenser eller ser på disse potensene er det som heter standardform.
Og det kan vi definere på denne måten her.
Det ser litt mystisk ut, men vi skal komme til noen eksempler rett etterpå. Det er et tall A ganger ti opphøyd i et annet tall B, men det tallet A må ligge mellom én og ti.
Større eller lik én og mindre enn ti. Og tallet B, her står det at B er medlem av, eller 'member of', Z, og Z det er hele tall. Det kan være positive og negative hele tall, eller null.
Vi ser hva det betyr i praksis, for det ser kanskje litt mystisk ut nå.
Tjuefem tusen, det kan vi skrive som to komma fem.
Ganger ti tusen.
Og ti tusen er jo ti opphøyd i fjerde, så da blir det to komma fem ganger ti i fjerde.
Da har vi det på standardform. Tallet to komma fem, det ligger mellom én og ti, og fire er et helt tall, ti opphøyd i fjerde.
Da har vi fått det på den standardformen.
Null komma null tre fire. Det kan vi skrive som tre komma fire.
Ganger noe lite. Skal vi se, ganger null komma null én blir det vel, og det blir tre komma fire. Unnskyld, tre komma fire ganger ti opphøyd i minus to, og det er fordi vi ser at det er to nuller her, og da blir det ti i minus andre.
Vi kan gå andre veien også. Hvis vi har et tall på standardform, så kan vi også gjøre det om til et vanlig tall. Ni komma ni to ganger ti i sjuende, det blir ni komma ni to ti opphøyd i sjuende, det er et tall fullt av sju nuller.
Og det blir, hva blir det? Det blir ni ni to.
Etter det første ni-tallet kommer.
Sju siffer: en, to, tre, fire, fem, seks, sju. Det ble et stort tall.
Det skal være nittini komma to millioner.
En komma null fire ganger ti i minus fjerde. På samme måten så blir det en komma null fire ganger null komma null null én ved siden av fire nuller her.
Og så blir det null komma null null null en null fire.
Man kan hoppe over den mellomlinjen hvis man finner ut av systemet her.
Riktig svar!
Man kan tenke seg at man øker den ene brøken med forholdet til den andre.
Riktig svar!
Man kan tenke seg at man flytter komma et hakk frem like mange ganger som potensen viser (når potensen er negativ).
Regn ut og skriv svaret på standardform
Riktig svar!
Regn ut og skriv svaret på standardform
Riktig svar!
Regn ut og skriv på standardform
Riktig svar!
Husk at man man trekker ifra eksponentene når man deler to potenser med samme grunntall på hverandre.
Regn ut og skriv svaret på standardform
Riktig svar!
Regn ut og skriv svaret på standardform
Riktig svar!
Rekn ut og skriv svaret på standardform
Riktig svar!
Riktig!
På tallinjen ovenfor er det merket av 12 punkter. Hvert av tallene nedenfor tilsvarer ett av punktene A –L på tallinjen.
Regn ut eller forklar hvor hvert av tallene skal plasseres.
- 1)
- 2)
- 3)
- 4)
- 5)
- 6)
Riktig svar!
1)
2)
3)
4)
5)
6)
Riktig svar!
\begin{align} 4^2 \cdot 2^{-3} \cdot 27^{\frac{1}{3}} \cdot 64^{-\frac{2}{3}} \\\ = \frac{4^2 \cdot 3}{2^3 \cdot \sqrt[3]{64^2}} \\\ = \frac{4^2 \cdot 3}{2^3 \cdot 4^2} \\\ = \frac{3}{8} \end{align}
Riktig svar!
Ja fordi
Riktig svar!
Ja, man kan også tenke det som
Riktig svar!
Det er slik det er definert, og det er noe man bare må huske.
Regn ut og skriv svaret så enkelt som mulig
Riktig svar!
Riktig svar!
Ja, man kan tenke seg at man må gange tallet tre ganger seg selv for å få . Og er da det å ta tredjeroten av .
Regn ut og skriv svaret så enkelt som mulig
a)
b)
Riktig svar!
Regn ut og skriv svaret så enkelt som mulig
Riktig svar!
Regn ut og skriv svaret så enkelt som mulig
a)
b)
Riktig svar!
Riktig svar!
Fordi
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Forklar hvorfor hver av påstandene nedenfor er riktige.
a)
b)
c)
som er større enn 2.
a) Vis at: 1) 2)
b) Vis eller forklar at
Gitt trekanten ABC nedenfor.
c) Bestem en eksakt verdi for lengden BC.
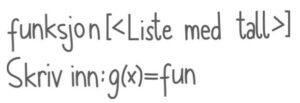
Flott opplegg og undervisning😊
Tusen takk!
Gjorde unna R2 som privatist på et halvt år!! Mattevideo har gjort det mye lettere å fordøye et så tungt pensum på så kort tid. Tusen takk for hjelpa!!😊
Bra undervisning!
Jeg er fornøyd med videone deres det har hjulpet meg til å bestå matten i både Vgs og Uni . Så takk😊
Meget bra!
Tusen takk. Veldig flink lærer. Gode forklaringer.
Helt topp :D
Bra side.
Kjempebra!😊
Bra side. Veldig gode forklaringer😊
Tror dette kommer til å redde meg på noen prøver fremover. Takk! :D
takk for hjelpen
Takk for læreren av denne siden. Det er utrolig en bra side, fikk meg mye. Tusen hjertelig takk
Kan trygt anbefale Arne Hovland! Beste læreren jeg har hatt i løpet av drøyt 20 år med utdanning.
takk for denne siden :D min 1T mattelærer snakker så monotont og gjør matte så kjedelig at interessen svinner vekk og jeg sovner etter 5 minutter.