
1 - 2 - 3 klasse

Lær VGS matten fra A til Å
med de beste metodene


Enkelt å
holde fokus



Forstå det
vanskelige


Få god
oversikt


Øv på
riktig tema


Få hjelp når
du stopper opp












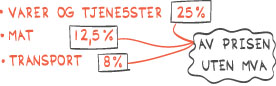


Oppgave 1 (4 poeng)

a) Hvor mange mil var kjøreturen?
Bilen kan kjøre 300 km når batteriet er 100 % oppladet.b) Hvor mange kilometer kan bilen kjøre når batteriet er 60 % oppladet?
Oppgave 2 (4 poeng)
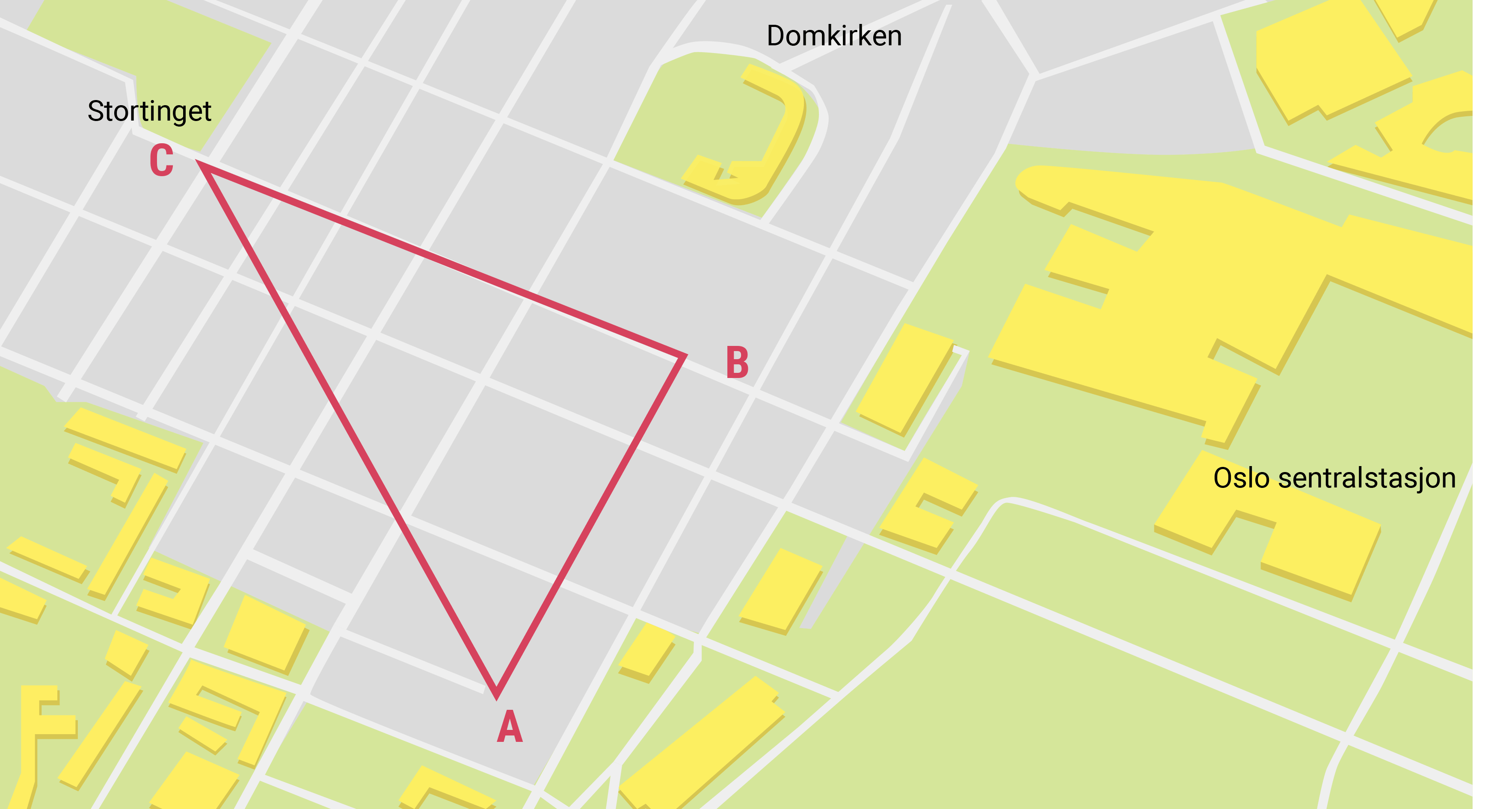
a) Bestem lengden AC på kartet.
Eva skal gå fra A til B, og så til C. Kartet har målestokken 1:5000.b) Hvor mange meter må Eva gå i virkeligheten?
Oppgave 3 (3 poeng)
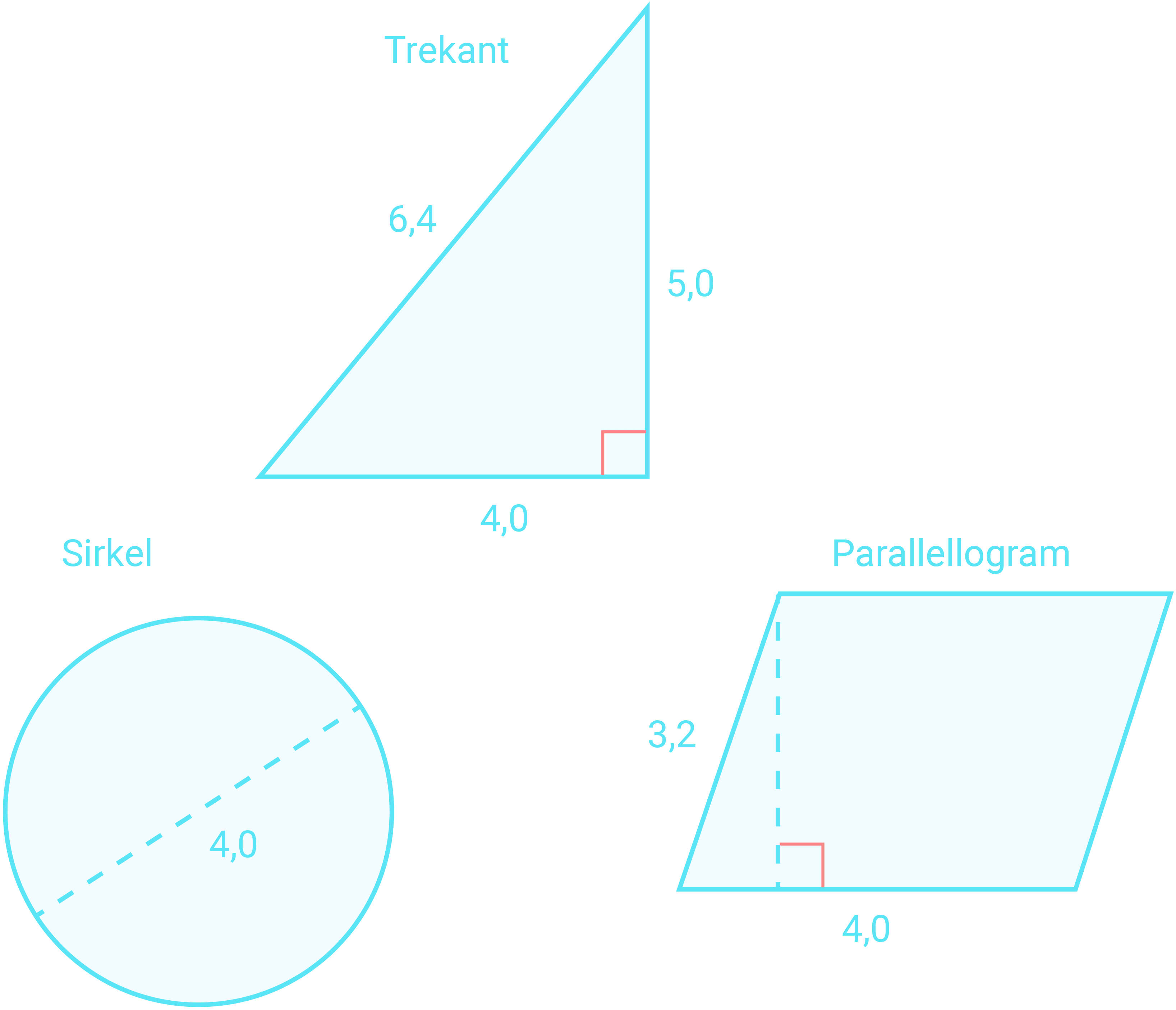
Oppgave 4 (3 poeng)
a) Løs likningen.b) Trekk sammen.
Oppgave 5 (4 poeng)


a) Bestem prisen per tur dersom han kjører 5 turer.
Bruk prisene på heiskort for voksne.b) Undersøk om prisen per dag og antall dager er proporsjonale størrelser.
Oppgave 6 (6 poeng)

a) Hvor mange kilogram reker kjøper Ole?
Det er 30 % spiselig del i reker. Resten er skall.b) Hvor mange gram er spiselig, og hvor mange gram er skall i 500 g reker?
I 2017 ble det fisket til sammen 16 000 tonn reker og kongekrabber i Norge. Forholdet mellom reker og kongekrabber var 7:1.c) Hvor mange tonn reker ble fisket i 2017?
Oppgave 7 (8 poeng)
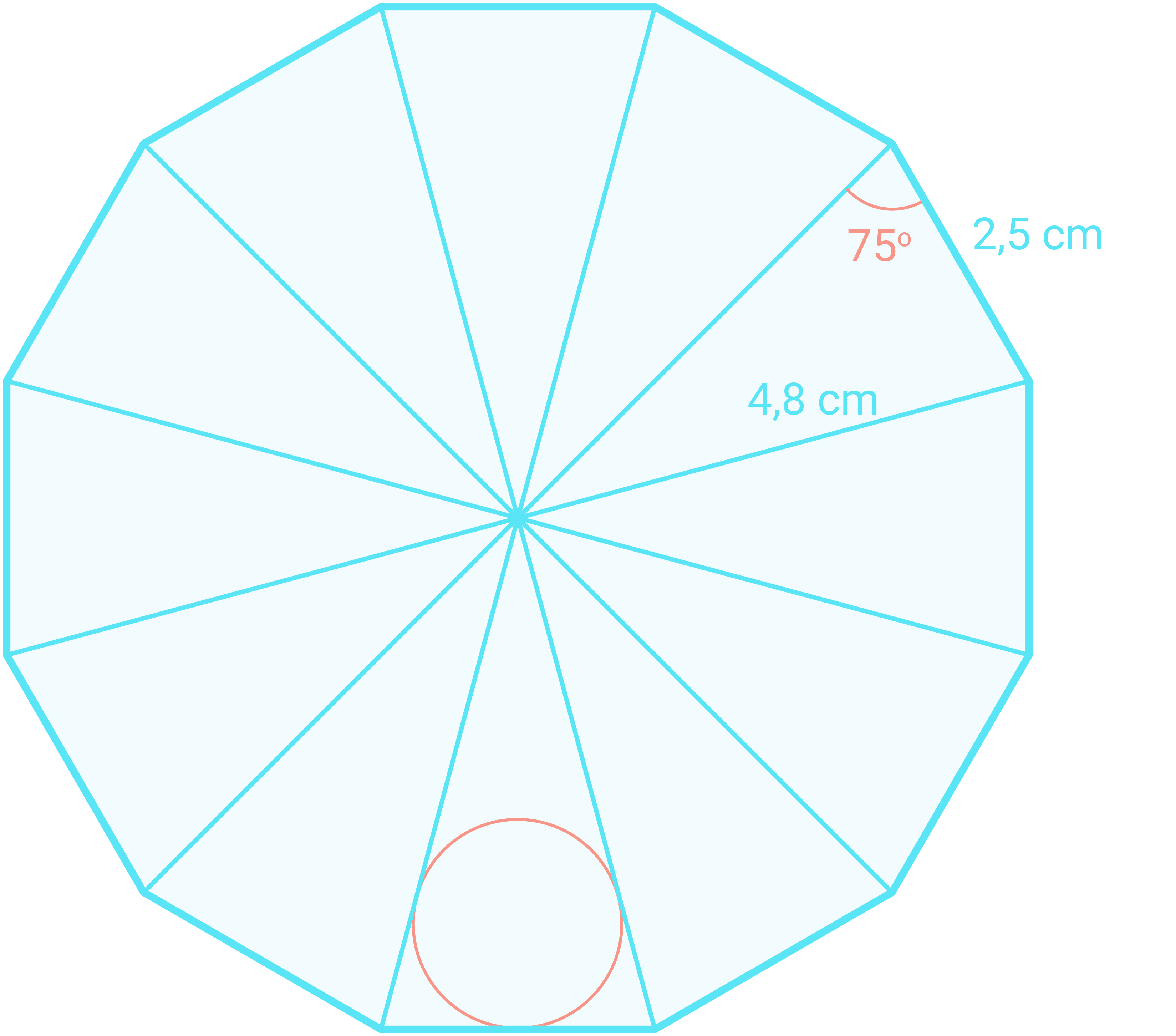

a) Bestem omkretsen av sølvstykket.
Sølvstykket merkes slik at det består av 12 like trekanter, slik figuren ovenfor viser.b) Bestem vinklene og høyden i en slik trekant.
Sølvsmeden stanser ut et hull i hver av de 12 trekantene. Diameteren i hvert hull er 1,7 cm.c) Vis at arealet av sølvstykket nå er 42 cm2.
Massetettheten til sølv er 10,5 g/cm3. Sølv koster 3,25 kr per gram.d) Hva koster sølvet i sølvstykket med hull når tykkelsen er 0,1 cm?
Oppgave 8 (6 poeng)

a) Bestem bruttolønna denne måneden.
Hege betaler 20 % i skatt per måned. I tillegg betaler hun 150 kr til fagforeningen.b) Bestem nettolønna.
Hege har opptjent 3128 kr i feriepenger. Feriepenger utgjør 12,5 % av feriepengegrunnlaget.c) Bestem feriepengegrunnlaget.
Oppgave 9 (6 poeng)

a) Hvor lang tid bruker dresinen fra Veggli til Rødberg?
Det kostet omtrent 30 millioner kroner å bygge Numedalsbanen i 1927. Da var konsumprisindeksen 3,5. I 2017 var den 105,5.b) Hva ville det kostet å bygge Numedalbanen i 2017 dersom prisen hadde fulgt konsumprisindeksen?
Et år var verdien av et lokomotiv 20 millioner kroner. Verdien synker med 9 % hvert år.c) Bestem verdien av lokomotivet etter tre år.
Oppgave 10 (6 poeng)

a) Vis at svømmebassenget rommer 2 500 000 L vann.
Fra klokken 08:00 tømmes svømmebassenget med 3800 L vann per minutt.b) Hva er klokken når svømmebassenget er tømt?
Svømmebassenget bygges om, slik at den ene enden av bassenget blir dypere. Figuren nedenfor viser det nye bassenget sett fra siden.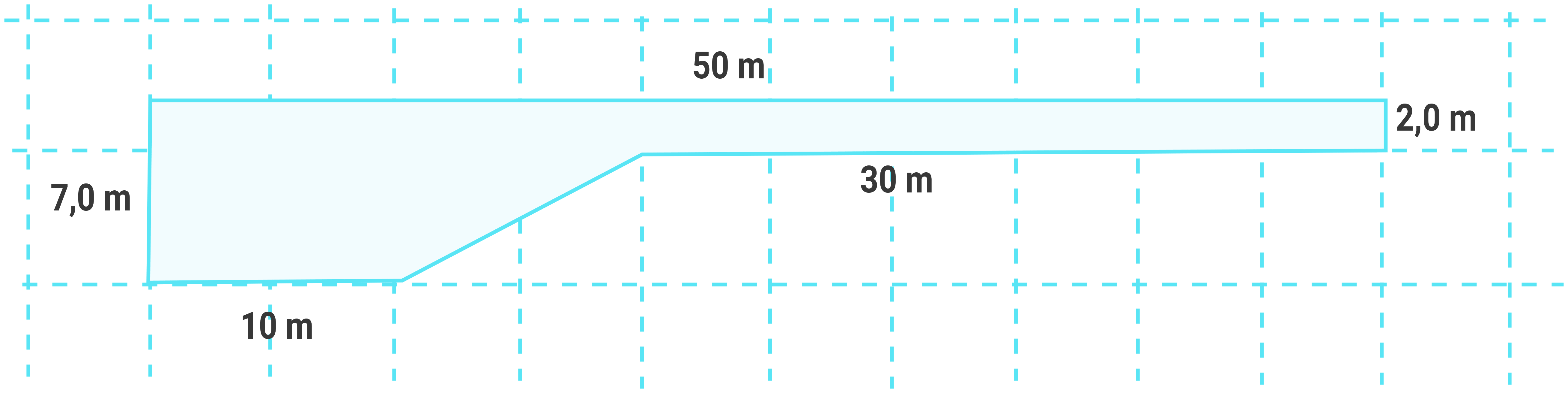
c) Hvor mange liter kan bassenget romme nå?
Oppgave 11 (4 poeng)
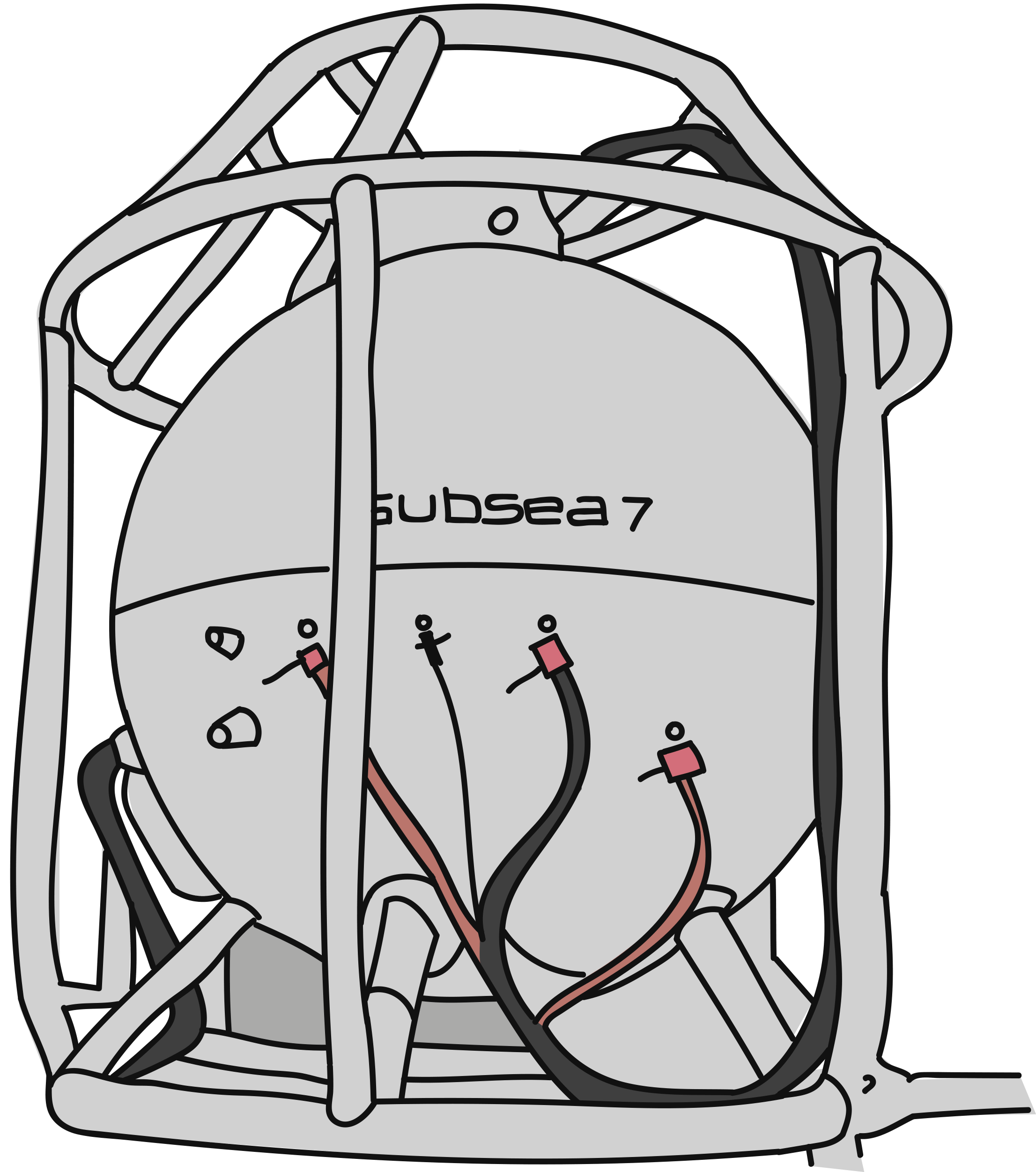

a) Bestem det indre volumet av dykkerklokken.
Dykkerklokken er laget av jern. Jern veier 7990 kilogram per kubikkmeter.b) Bestem hvor mye jernet i dykkerklokken veier.
Oppgave 12 (6 poeng)
Anne har begynt å spare til en egen gård i Gårdssparing for unge (GSU). Hun setter inn 15 000 kr den 1. januar hvert år fra og med 2015, og får 4,50 % rente per år.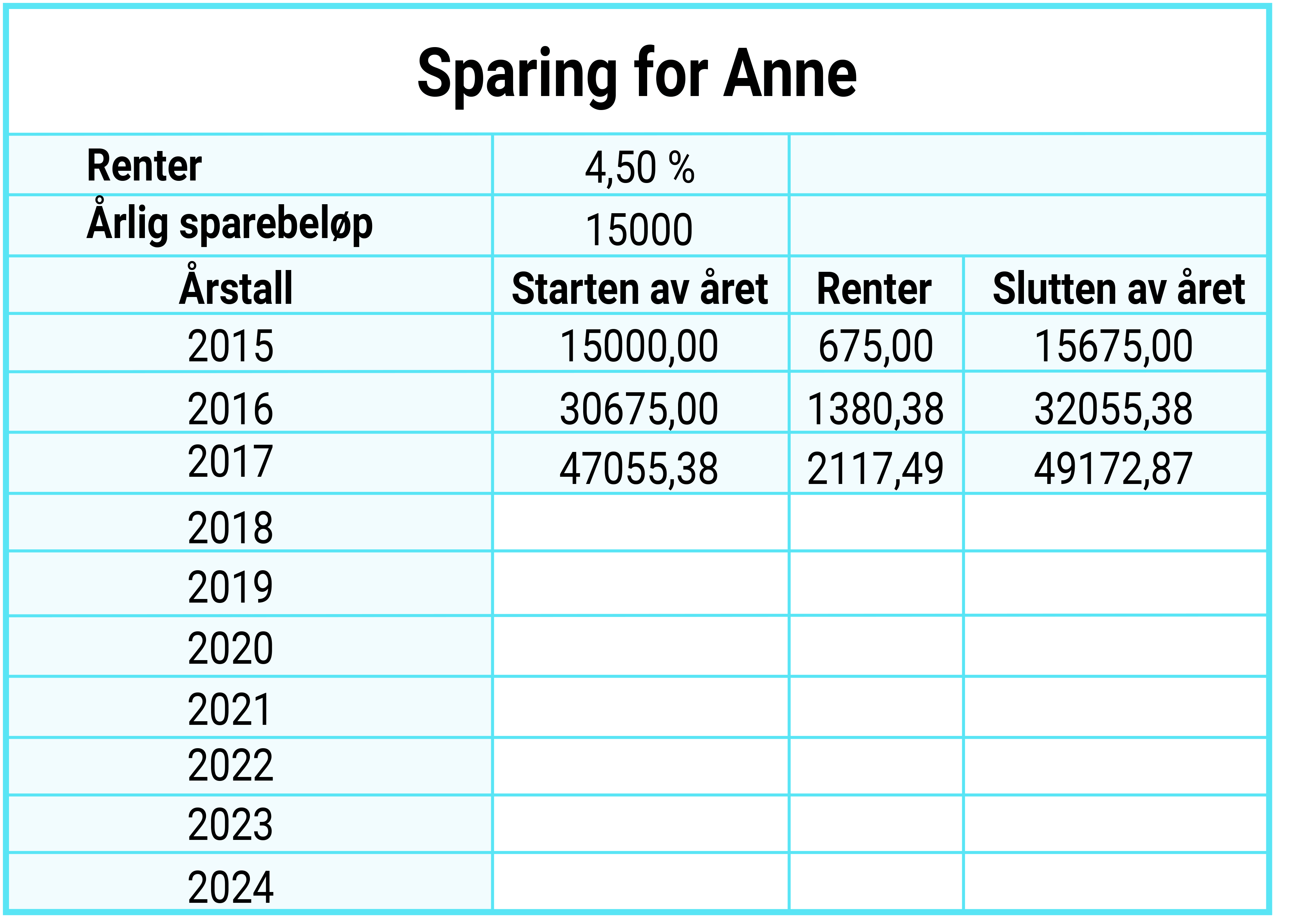
a) Bruk regneark, fyll inn og fullfør sparingsplanen for Anne til og med år 2024.
b) Hvor mange kroner vil Anne få i renter fra 2015 til og med 2024?
c) Hvor mange kroner ville Anne hatt på kontoen dersom hun heller hadde spart 30 000 kr per år fra 2015?
Husk å bruke formler og vise dem i besvarelsen.Prøvesmak våre videoer
Mattevideo tilbyr fullstendig dekning av kursene 1P, 1PY, 1T, 2P, S1, R1, S2 og R2 innenfor videregående skole. Under har vi lagt ut noen smakebiter fra disse kursene, så du kan sjekke ut noe av det vi har å by på, før du bestemmer deg for å bli abonnent.1P - Polynomfunksjoner1PY - Prosentregning1T - Funksjonsbegrepet2P - Første gradS1 - LikningssettR1 - Å finn den deriverte ved å bruke derivasjonsreglerS2 - Aritmetiske og geometriske rekkerR2 - Sinusfunksjoner og cosinusfunksjoner

Lær å jobbe smarterepå 5 minutter
Det finnes mange ulike studieteknikker, utfordringen er ofte å finne de som fungerer best for deg. I oversikten under finner du enkelt de beste teknikkene.
Alle våre studietips er laget av vår superelev - med 6 i snitt fra vgs. Ingen av artiklene tar mer enn 5 minutter å lese - slik at du kan starte læringen så fort som mulig.
Hva skjer i hjernen når du lærer?
 Du møter noe nytt for første gang
Du møter noe nytt for første gang Du kobler den nye tingen med kunnskap du har fra før
Du kobler den nye tingen med kunnskap du har fra før Du repeter og styrker sammenhengene
Du repeter og styrker sammenhengene Du bruker kunnskapen
Du bruker kunnskapen

Vanlige utfordringer - og hvordan løse dem


Teknikkene som gjør deg til en superelev
La oss ringe deg, så finner vi en god løsning.




























Flott opplegg og undervisning😊
Tusen takk!
Gjorde unna R2 som privatist på et halvt år!! Mattevideo har gjort det mye lettere å fordøye et så tungt pensum på så kort tid. Tusen takk for hjelpa!!😊
Bra undervisning!
Jeg er fornøyd med videone deres det har hjulpet meg til å bestå matten i både Vgs og Uni . Så takk😊
Meget bra!
Tusen takk. Veldig flink lærer. Gode forklaringer.
Helt topp :D
Bra side.
Kjempebra!😊
Bra side. Veldig gode forklaringer😊
Tror dette kommer til å redde meg på noen prøver fremover. Takk! :D
takk for hjelpen
Takk for læreren av denne siden. Det er utrolig en bra side, fikk meg mye. Tusen hjertelig takk
Kan trygt anbefale Arne Hovland! Beste læreren jeg har hatt i løpet av drøyt 20 år med utdanning.
takk for denne siden :D min 1T mattelærer snakker så monotont og gjør matte så kjedelig at interessen svinner vekk og jeg sovner etter 5 minutter.