
VGS matematikk
1 - 2 - 3 klasse
1 - 2 - 3 klasse

Lær VGS matten fra A til Å
med de beste metodene


Enkelt å
holde fokus



Forstå det
vanskelige


Få god
oversikt


Øv på
riktig tema


Få hjelp når
du stopper opp

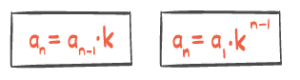
Følger og rekker
07:59

21:40

10:59
28:08

36:09
43:52
20:59
28:33

28:45
49:28
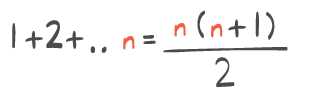
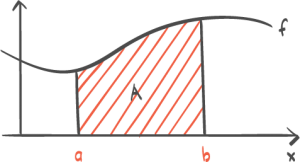
Integralregning
07:38
08:24
01:11
07:52
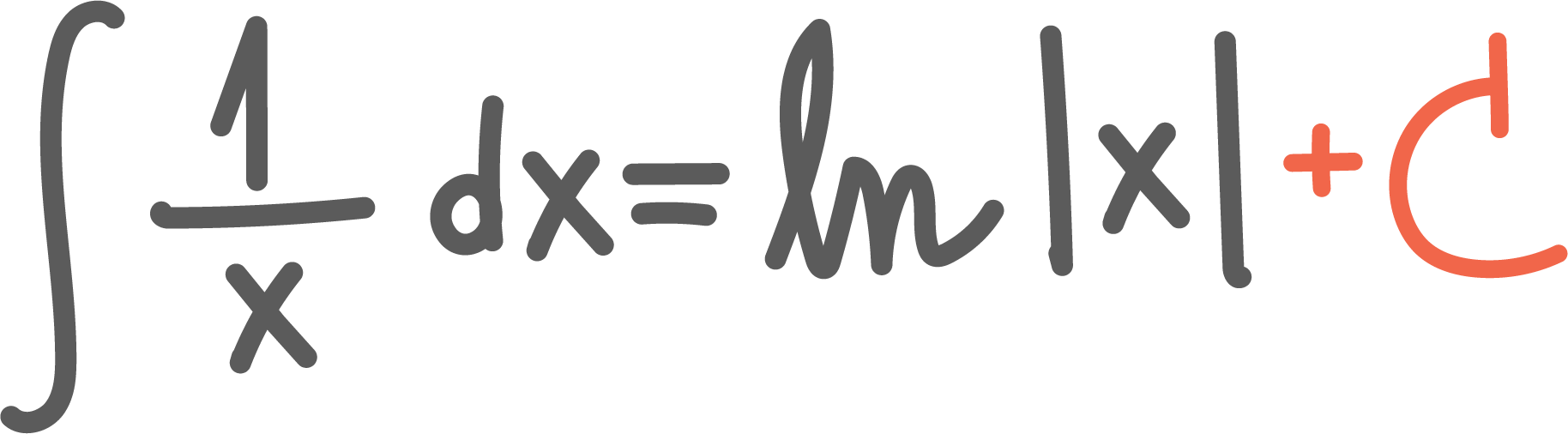
30:41
10:26
04:27
34:04
28:47
13:11
20:05
Integrasjonsmetoder
15:05

09:24
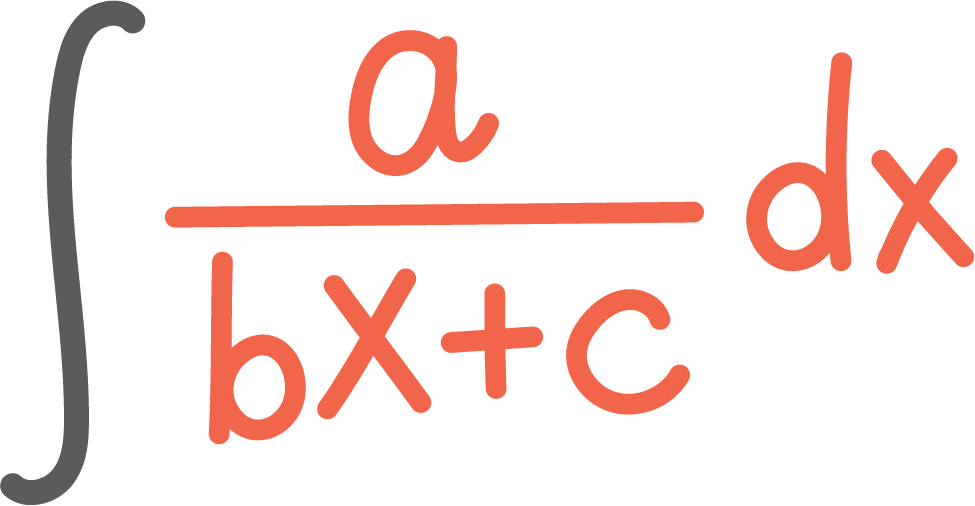
21:10
08:40
16:57
09:55

23:29
27:42
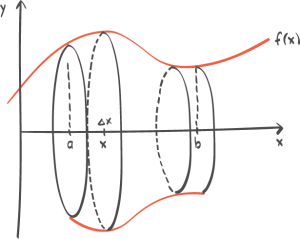
07:34
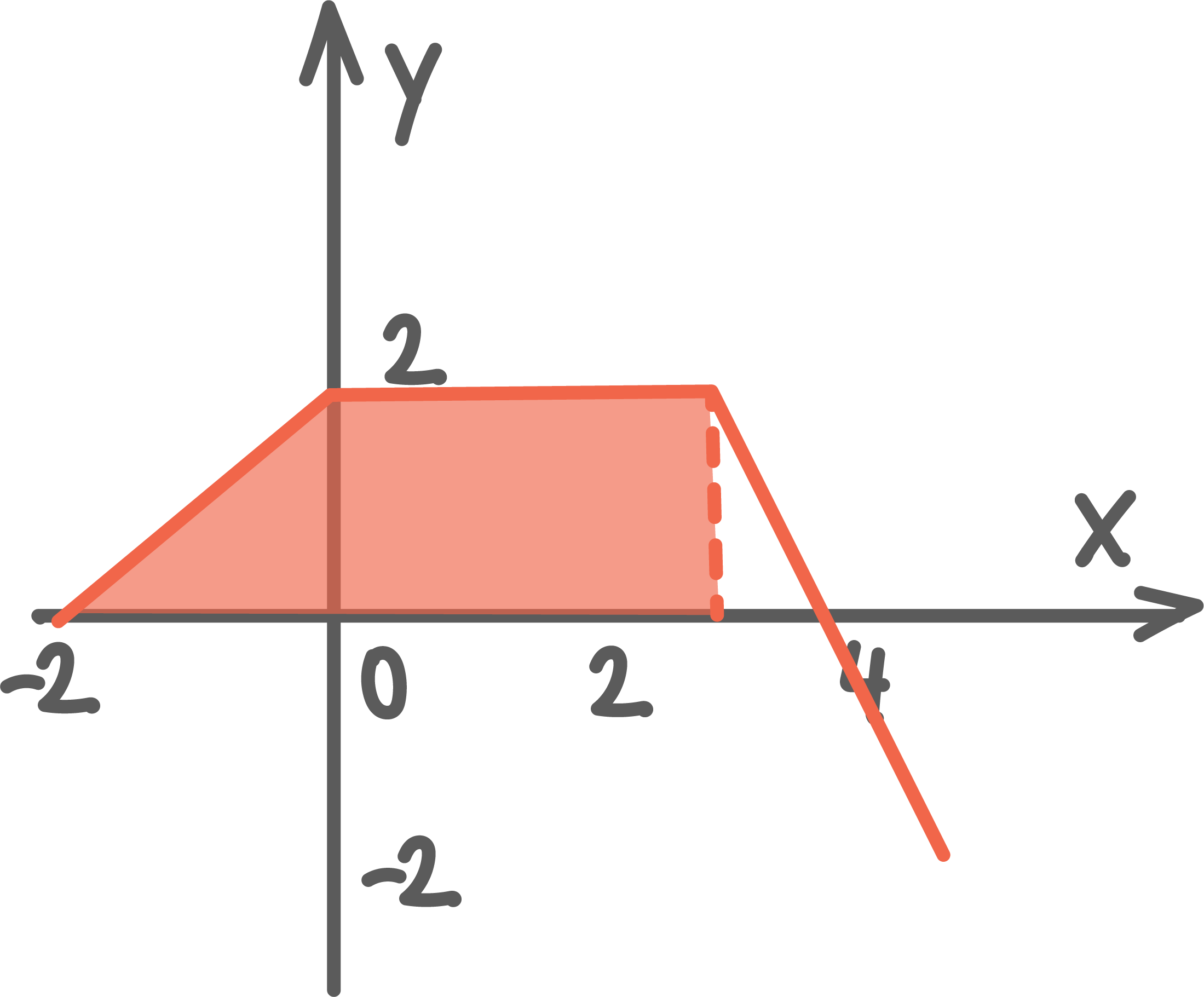
07:31
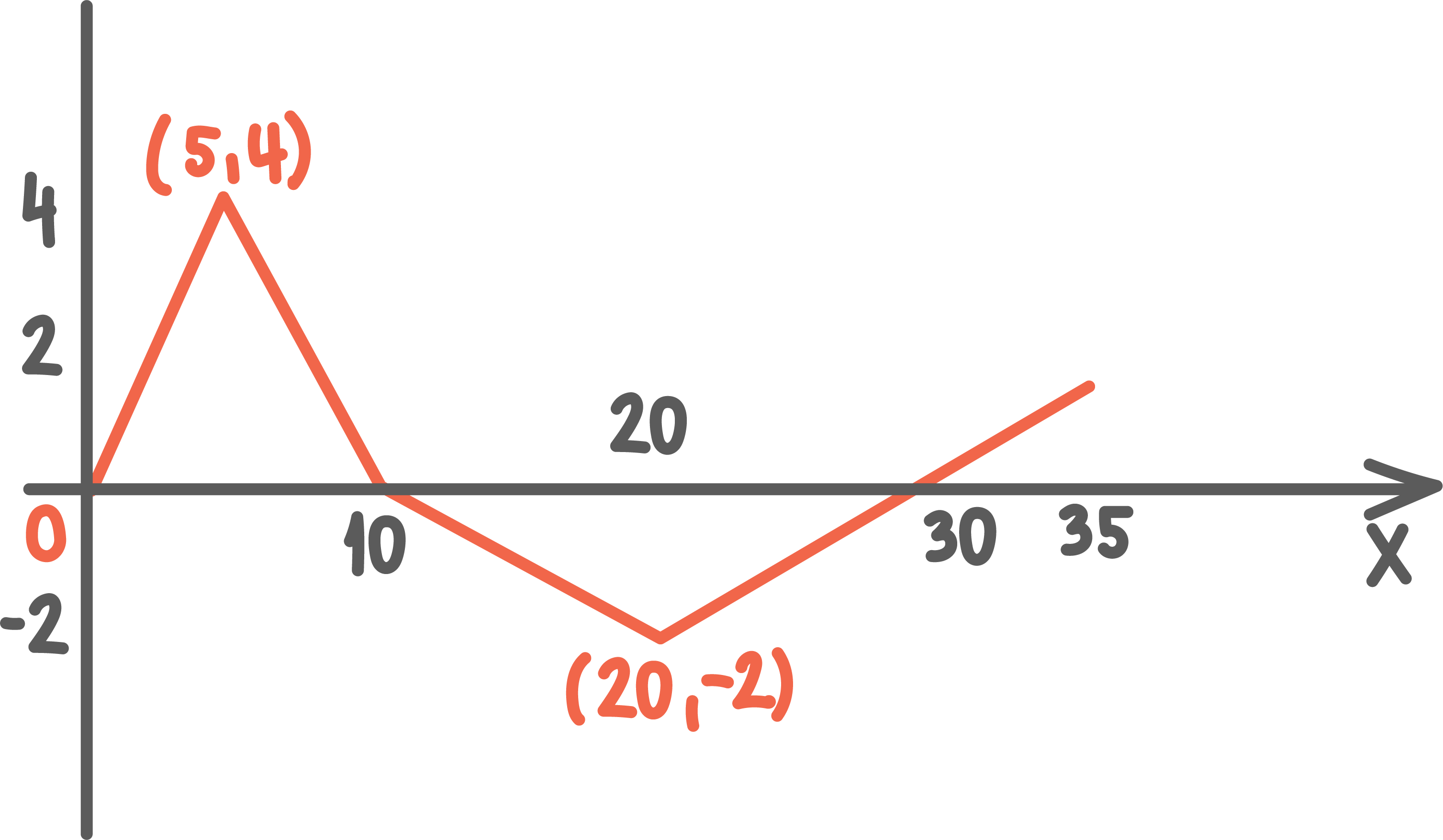
Vektorer
02:35
03:31
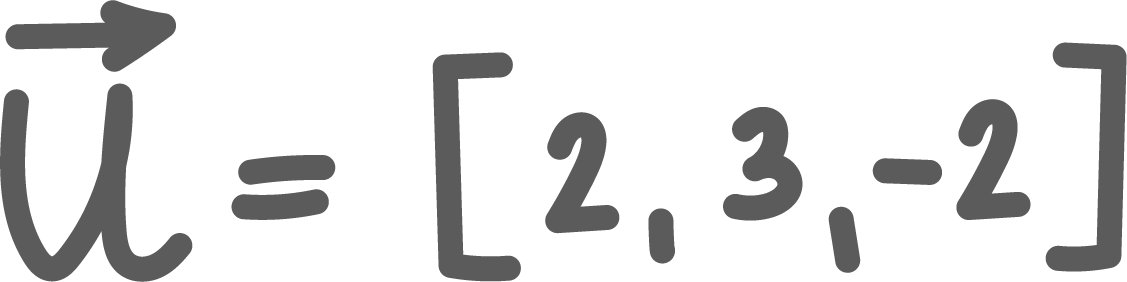
07:57
03:14

41:39
15:07

17:35
34:30

14:04
12:49

59:28
30:16
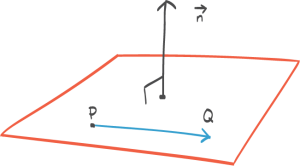
37:45
11:48
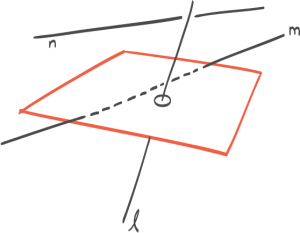
27:40
16:06
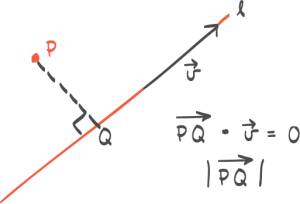
Trigonometri
19:21
08:45

21:24
03:26
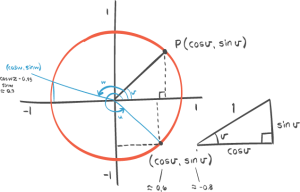
13:21
09:44
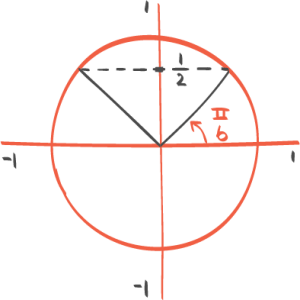
03:30
11:22
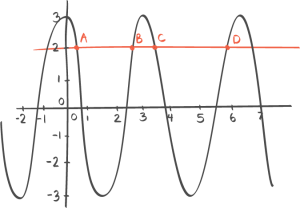
03:06
15:54
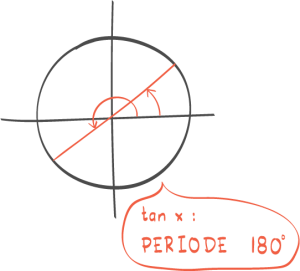
19:22
17:23
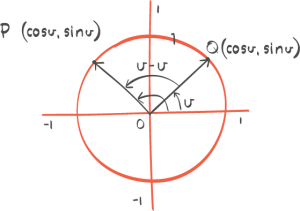
Funksjoner og kurver
13:18
05:28
39:37
13:44
07:04
14:29
04:15

Eksamenstid 5 timer
Del 1 (Uten hjelpemidler) skal leveres etter 2 timer.
Del 2 (Med hjelpemidler) skal leveres etter senest 5 timer.

Oppgåve 1 (4 poeng)
Deriver funksjonane a) b) c)Oppgåve 2 (4 poeng)
Bestem integralet ved å bruke a) variabelskifte b) delbrøkoppspaltingOppgåve 3 (4 poeng)
Punkta A (1,-1,0), B(3,1,1), og C(0,0,0) er gitt. a) Bestem . Bruk resultatet til å bestemme arealet av b) Bestem . Bruk mellom anna dette resultatet til å bestemme arealet avOppgåve 4 (3 poeng)
Løys differensiallikninga y' = 6xy når y(0) = 2Oppgåve 5 (5 poeng)
Ei rekkje er gitt ved a) Bestem og b) Forklar at rekkja er aritmetisk, og bruk dette til å finne eit uttrykk for og . c) Bestem kor mange ledd rekkja minst må ha for atOppgåve 6 (2 poeng)
Denne informasjonen er gitt om ein kontinuerleg funksjon f : • for alle • for alle • for x = -2 og for x = 2 • for x = 1 og for x = 3 Lag ei skisse som viser korleis grafen til f kan sjå ut.Oppgåve 7 (2 poeng)
Bruk induksjon til å bevise påstanden
Oppgåve 1 (4 poeng)
Ein pasient får 8 mL av ein medisin kvar time. Den totale mengda medisin i kroppen t timar etter at medisineringa starta, er y(t) mL. I løpet av ein time skil kroppen ut 5 % av den totale medisinmengda. a) Forklar at b) Vis at når y (0) = 0 c) Bestem . Kommenter svaret.Oppgåve 2 (6 poeng)
Funksjonen f er gitt ved a) Teikn grafen til f . b) Bestem eventuelle topp- og botnpunkt på grafen til f. c) Bestem arealet som er avgrensa av grafen til f og x-aksen.Oppgåve 3 (8 poeng)
Skissa nedanfor viser ein pyramide OABCD som er plassert i eit romkoordinatsystem. Hjørna i pyramiden er O(0,0,0) , A(3,0,0) , B(3,3,0) , C(0,3,0) og D(0,0,4)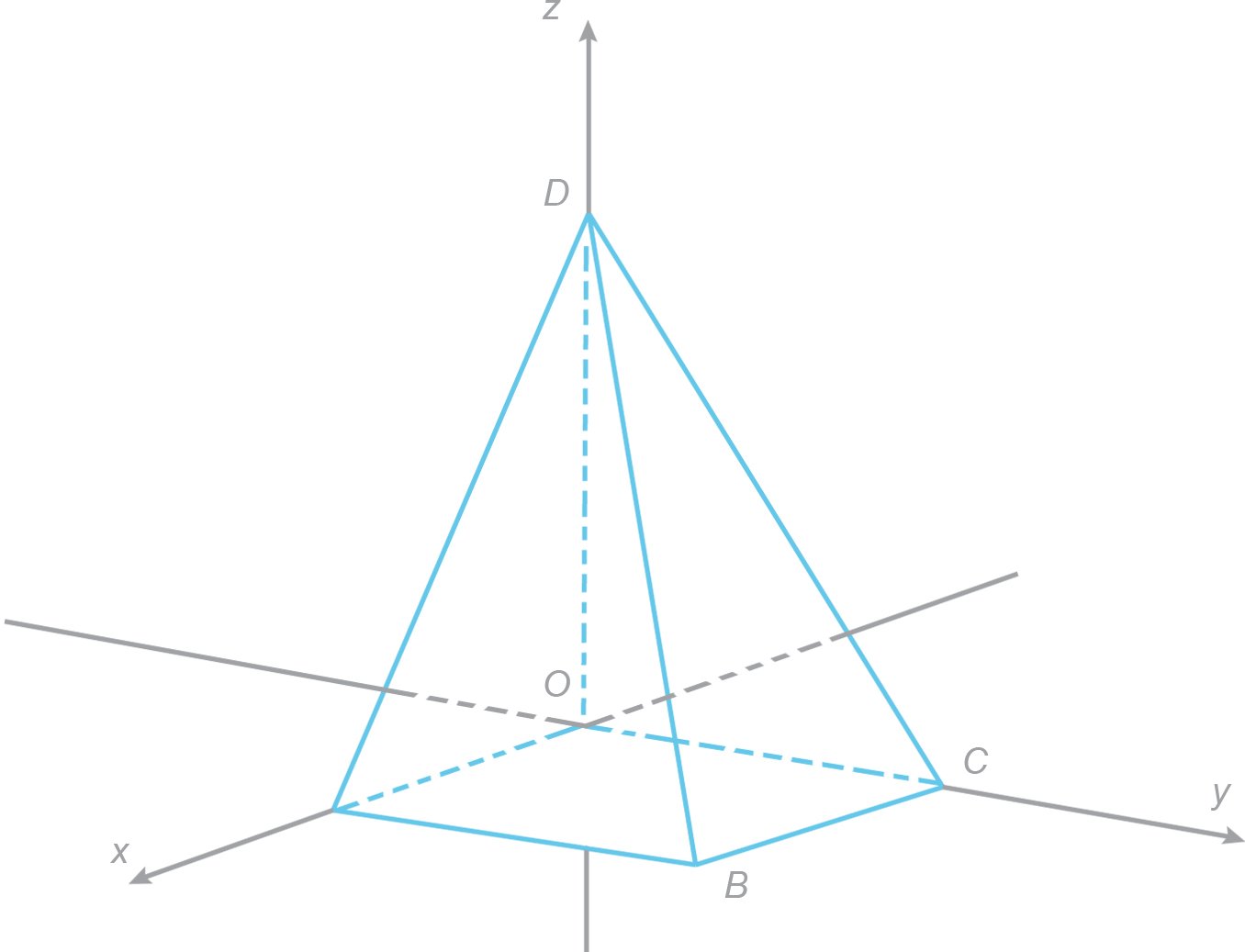 a) Bestem ved rekning arealet av sideflata ABD i pyramiden.
b) Sideflata ABD ligg i eit plan ?.
Vis ved rekning at planet ? har likninga
4x + 3z - 12 = 0
c) Bestem avstanden frå punktet O til planet ?.
d) Bestem ved rekning vinkelen mellom dei to plana som sideflatene ABD og BCD ligg i.
a) Bestem ved rekning arealet av sideflata ABD i pyramiden.
b) Sideflata ABD ligg i eit plan ?.
Vis ved rekning at planet ? har likninga
4x + 3z - 12 = 0
c) Bestem avstanden frå punktet O til planet ?.
d) Bestem ved rekning vinkelen mellom dei to plana som sideflatene ABD og BCD ligg i.
Oppgåve 4 (6 poeng)
Figuren nedanfor viser ein sirkelsektor OBC der C ligg i første kvadrant. Bogen BC er ein del av sirkelen med likning . Punktet A har koordinatane (2,0) og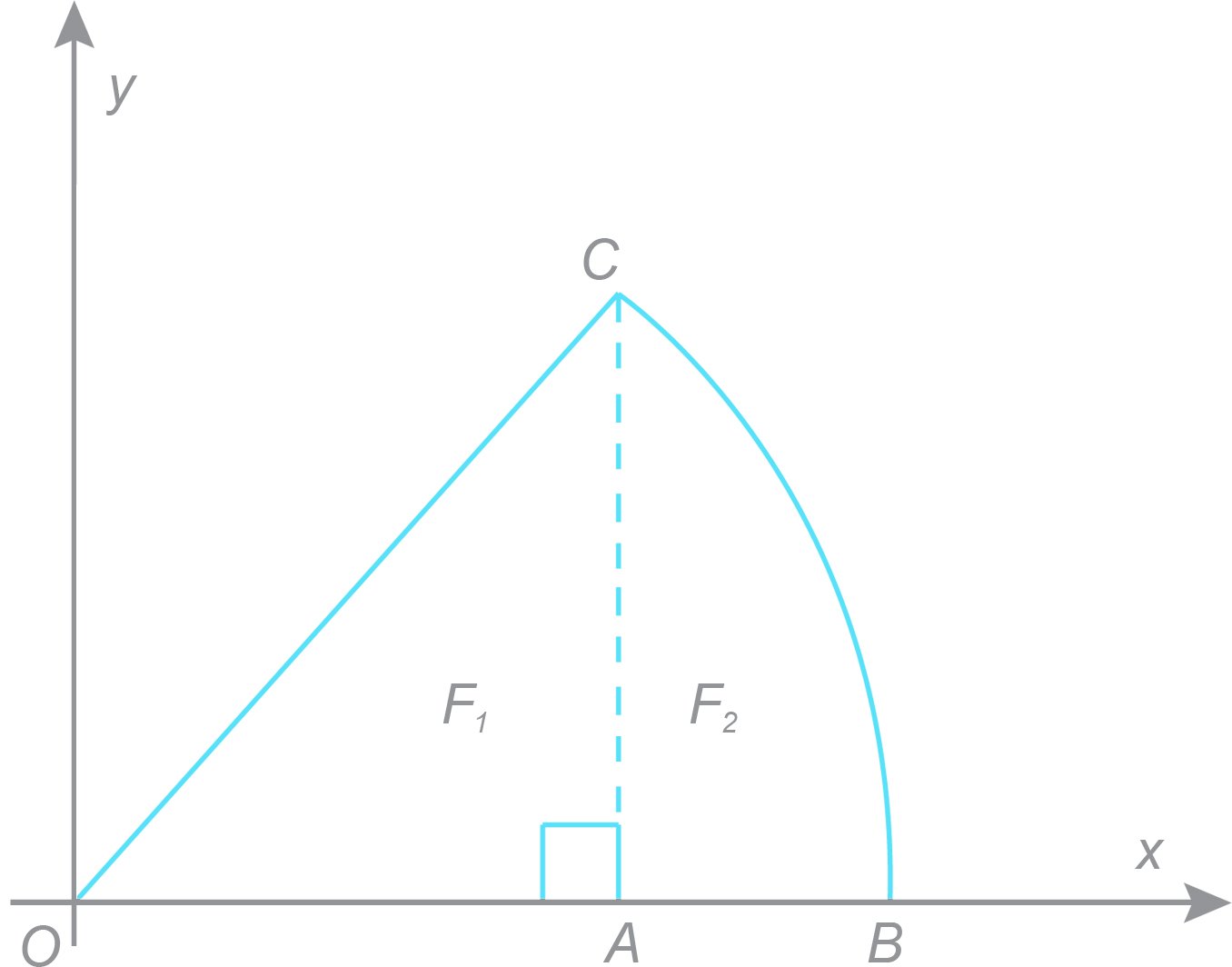 a) Vis at koordinatane til C er .
Bestem likninga for den rette linja gjennom O og C.
b) Når flatestykket blir dreidd 360° om x-aksen, får vi ei kjegle.
Bestem volumet av denne kjegla ved hjelp av integralrekning.
c) Når flatestykket blir dreidd 360° om x-aksen, får vi eit kulesegment.
Bestem volumet av dette kulesegmentet ved hjelp av integralrekning.
a) Vis at koordinatane til C er .
Bestem likninga for den rette linja gjennom O og C.
b) Når flatestykket blir dreidd 360° om x-aksen, får vi ei kjegle.
Bestem volumet av denne kjegla ved hjelp av integralrekning.
c) Når flatestykket blir dreidd 360° om x-aksen, får vi eit kulesegment.
Bestem volumet av dette kulesegmentet ved hjelp av integralrekning.
Oppgåve 5 (6 poeng)
På figuren er eit rektangel med sider x og y skrive inn i ein sirkel. Sirkelen har diameteren D. ?v er vinkelen mellom x og D.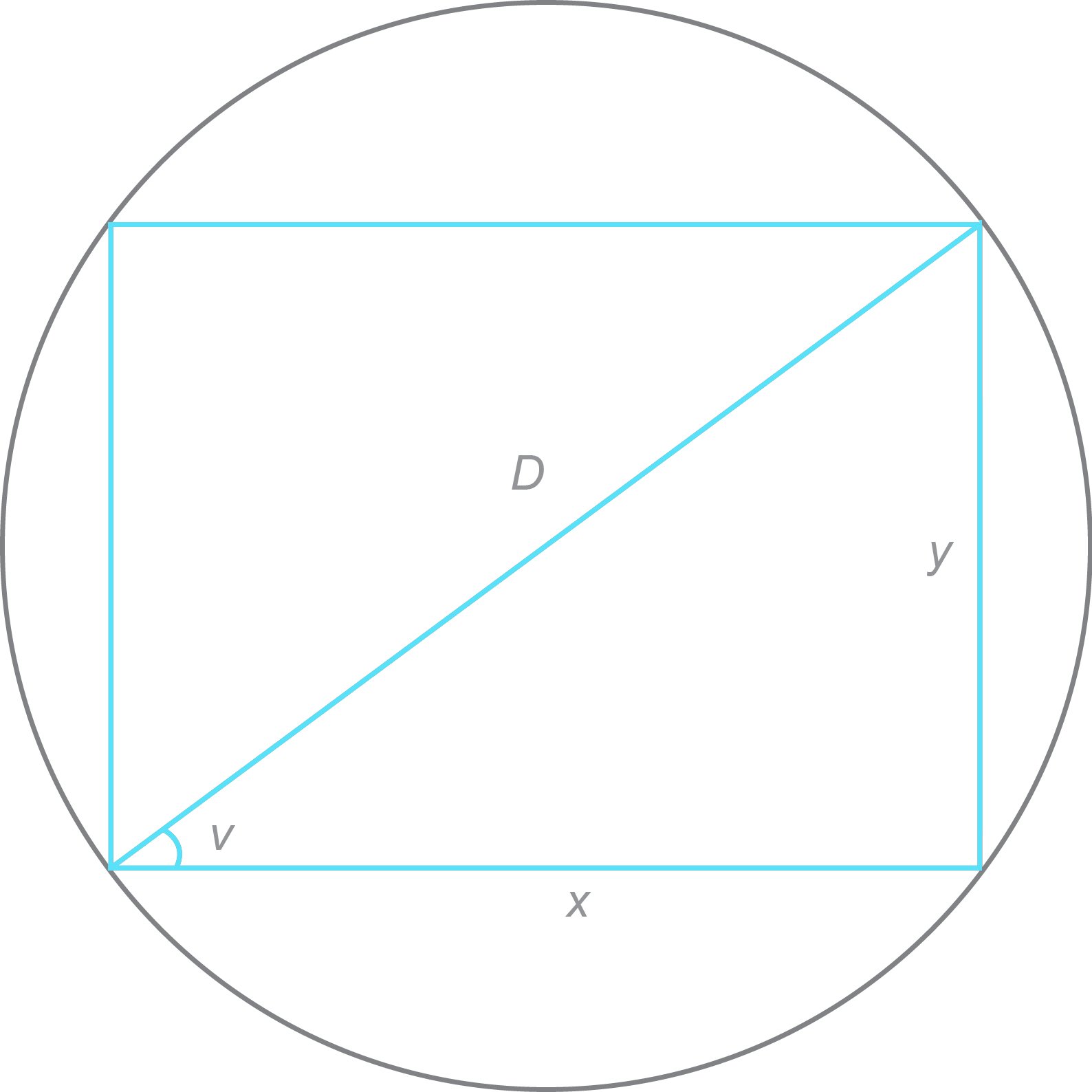 a) Forklar at omkretsen O til rektangelet kan skrivast som
O(v) = 2Dcosv + 2Dsinv
Bestem eit funksjonsuttrykk for arealet A(v) av rektangelet.
b) Bruk O'(v) og vis at det rektangelet som har størst omkrets, er eit kvadrat.
Bestem den største omkretsen av rektangelet uttrykt ved diameteren D.
c) Bruk A'(v) og vis at det rektangelet som har størst areal, også er eit kvadrat.
Bestem det største arealet av rektangelet uttrykt ved diameteren D.
a) Forklar at omkretsen O til rektangelet kan skrivast som
O(v) = 2Dcosv + 2Dsinv
Bestem eit funksjonsuttrykk for arealet A(v) av rektangelet.
b) Bruk O'(v) og vis at det rektangelet som har størst omkrets, er eit kvadrat.
Bestem den største omkretsen av rektangelet uttrykt ved diameteren D.
c) Bruk A'(v) og vis at det rektangelet som har størst areal, også er eit kvadrat.
Bestem det største arealet av rektangelet uttrykt ved diameteren D.
Oppgåve 6 (6 poeng)
Sierpi?ski-trekanten, som har fått namnet sitt etter den polske matematikaren Wac?aw Franciszek Sierpi?ski (1882–1969), lagar vi slik: 1. Vi startar med ein likesida, svart trekant har areal A. Sjå figur 1. 2. Midtpunktet på kvar av sidene i trekanten er hjørna i ein ny kvit, likesida trekant. Denne kvite trekanten fjernar vi. Vi står da igjen med tre likesida, svarte trekantar. Sjå figur 2. 3. Vi gjentek denne prosessen med kvar av dei svarte trekantane. Sjå figurane 3–5. Vi tenkjer oss at prosessen blir utført uendeleg mange gonger. Den «gjennomhola» figuren vi da står igjen med, blir kalla Sierpi?ski-trekanten.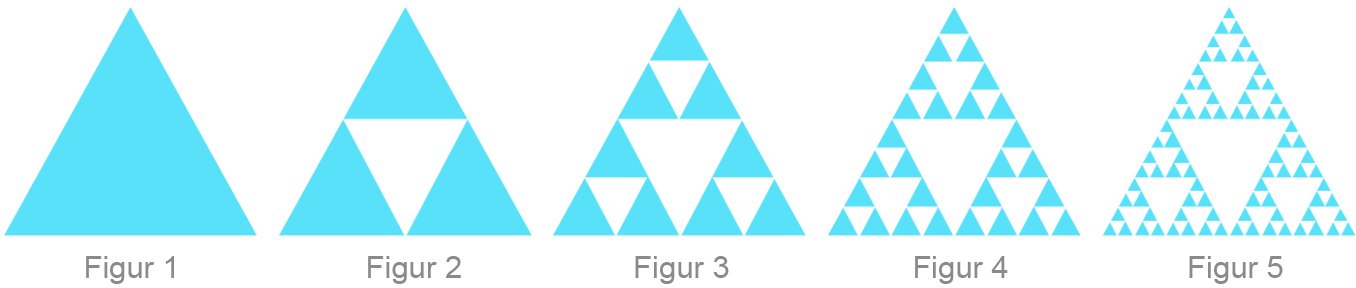 Summen av areala som blir fjerna (dei kvite trekantane), er gitt ved rekkja
a) Bestem summen av rekkja ovanfor.
Kva fortel svaret ditt om arealet av Sierpi?ski-trekanten?
b) Sidene i trekanten i figur 1 er lik a.
Forklar at omkretsane av dei svarte trekantane i figurane 25? ovanfor er høvesvis
og
c) Vi gjer prosessen som forklart i trinn 2 ovanfor n gonger. Forklar at omkretsen av dei svarte trekantane da er lik
Forklar at når
Kva fortel det om omkretsen til Sierpi?ski-trekanten?
Summen av areala som blir fjerna (dei kvite trekantane), er gitt ved rekkja
a) Bestem summen av rekkja ovanfor.
Kva fortel svaret ditt om arealet av Sierpi?ski-trekanten?
b) Sidene i trekanten i figur 1 er lik a.
Forklar at omkretsane av dei svarte trekantane i figurane 25? ovanfor er høvesvis
og
c) Vi gjer prosessen som forklart i trinn 2 ovanfor n gonger. Forklar at omkretsen av dei svarte trekantane da er lik
Forklar at når
Kva fortel det om omkretsen til Sierpi?ski-trekanten?
Gratis Prøvesmak
Superteknikker
En til en veiledning
Prøvesmak våre videoer
Mattevideo tilbyr fullstendig dekning av kursene 1P, 1PY, 1T, 2P, S1, R1, S2 og R2 innenfor videregående skole. Under har vi lagt ut noen smakebiter fra disse kursene, så du kan sjekke ut noe av det vi har å by på, før du bestemmer deg for å bli abonnent.1P - Polynomfunksjoner1PY - Prosentregning1T - Funksjonsbegrepet2P - Første gradS1 - LikningssettR1 - Å finn den deriverte ved å bruke derivasjonsreglerS2 - Aritmetiske og geometriske rekkerR2 - Sinusfunksjoner og cosinusfunksjoner

Lær å jobbe smarterepå 5 minutter
Det finnes mange ulike studieteknikker, utfordringen er ofte å finne de som fungerer best for deg. I oversikten under finner du enkelt de beste teknikkene.
Alle våre studietips er laget av vår superelev - med 6 i snitt fra vgs. Ingen av artiklene tar mer enn 5 minutter å lese - slik at du kan starte læringen så fort som mulig.
Hva skjer i hjernen når du lærer?
 Du møter noe nytt for første gang
Du møter noe nytt for første gang Du kobler den nye tingen med kunnskap du har fra før
Du kobler den nye tingen med kunnskap du har fra før Du repeter og styrker sammenhengene
Du repeter og styrker sammenhengene Du bruker kunnskapen
Du bruker kunnskapen

Vanlige utfordringer - og hvordan løse dem


Teknikkene som gjør deg til en superelev
En til en veiledning
Ønsker du en uforpliktende samtale om dine behov?
La oss ringe deg, så finner vi en god løsning.
La oss ringe deg, så finner vi en god løsning.

03:35
Oppgave 2

Vis ved å betrakte en kjegle som et omdreiningslegeme at volumet til en kjegle med radius og høyde er gitt ved .
01:48
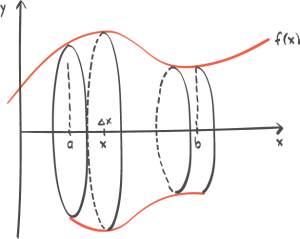
Teori 1

Hva er en omdreiningsfigur?

05:43
Teori 2

Vi regner volumet av et omdreiningslegeme dreiet om y-aksen.
02:38
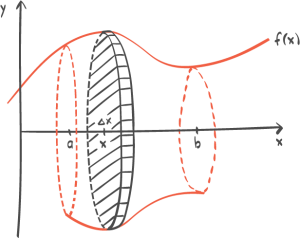
Teori 3

Volumet av en omdreiningsfigur.

05:52
Teori 4

Omdreiningsflater - hva det er og hvorfor formelen blir som den blir.
07:28
Teori 5

Vi tegner og regner. Gitt funksjonen
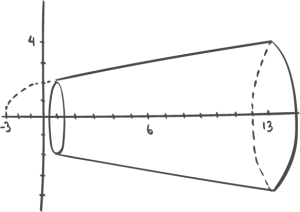
Tegn grafen og finn volumet av omdreiningsfiguren vi får ved å dreie grafen om x-aksen.

07:58
Oppgave 1

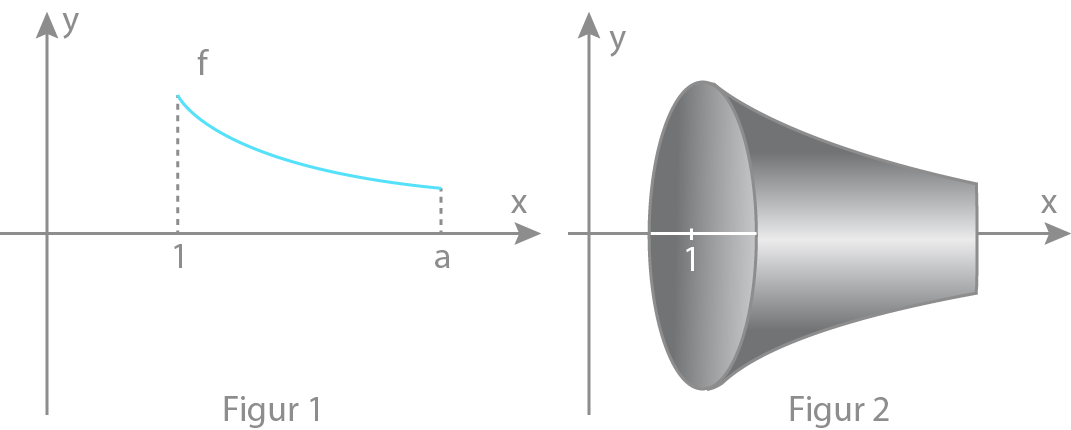
Gitt funksjonen .
a) Tegn grafen til f.
b) Finn et uttrykk for volumet av figuren vi får når vi dreier grafen om x-aksen.
c) Finn volumet når x = 2
d) Hva blir volumet av omdreiningsfiguren når t går mot uendelig?
a) Tegn grafen til f.
b) Finn et uttrykk for volumet av figuren vi får når vi dreier grafen om x-aksen.
c) Finn volumet når x = 2
d) Hva blir volumet av omdreiningsfiguren når t går mot uendelig?
07:33
Oppgave 3

Vis at volumet, , til en kule med radius , er gitt ved .
08:36
Oppgave 4

Ei stålkule har diameter og et hull i midten med diameter , tvers gjennom kulas sentrum. Stålet har tetthet . Hvor mye veier kula?




















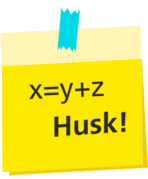















Flott opplegg og undervisning😊
Tusen takk!
Gjorde unna R2 som privatist på et halvt år!! Mattevideo har gjort det mye lettere å fordøye et så tungt pensum på så kort tid. Tusen takk for hjelpa!!😊
Bra undervisning!
Jeg er fornøyd med videone deres det har hjulpet meg til å bestå matten i både Vgs og Uni . Så takk😊
Meget bra!
Tusen takk. Veldig flink lærer. Gode forklaringer.
Helt topp :D
Bra side.
Kjempebra!😊
Bra side. Veldig gode forklaringer😊
Tror dette kommer til å redde meg på noen prøver fremover. Takk! :D
takk for hjelpen
Takk for læreren av denne siden. Det er utrolig en bra side, fikk meg mye. Tusen hjertelig takk
Kan trygt anbefale Arne Hovland! Beste læreren jeg har hatt i løpet av drøyt 20 år med utdanning.
takk for denne siden :D min 1T mattelærer snakker så monotont og gjør matte så kjedelig at interessen svinner vekk og jeg sovner etter 5 minutter.