VGS matematikk
1 - 2 - 3 klasse
1 - 2 - 3 klasse
Lær VGS matten fra A til Å
med de beste metodene
Enkelt å
holde fokus
Forstå det
vanskelige
Få god
oversikt
Øv på
riktig tema
Få hjelp når
du stopper opp
Vektorer & romgeometri
47:13
23:11
29:25
07:03
25:18
47:19
18:32
13:06
35:23
05:34
27:40
14:06
07:42
11:36
Tallfølger og rekker
09:41
15:19
02:19
08:08
05:02
19:30
10:17
17:10
14:47
28:33
08:26
16:24
Trigonometriske funk
31:20
03:26
13:30
10:48
27:33
07:02
19:22
05:54
18:56
30:28
13:18
32:51
28:58
Funksjoner og grafer
05:44
12:42
04:37
08:45
Integrasjon
07:47
10:26
12:45
13:07
37:50
15:14
44:57
22:29
11:54
07:58
Differensiallikninger
10:18
16:44
26:49
45:38
47:02
03:48
07:23
Eksamenstid 5 timer
Del 1 (Uten hjelpemidler) skal leveres etter 2 timer.
Del 2 (Med hjelpemidler) skal leveres etter senest 5 timer.
Oppgåve 1 (4 poeng)
Deriver funksjonane a) b) c)Oppgåve 2 (4 poeng)
Bestem integralet ved å bruke a) variabelskifte b) delbrøkoppspaltingOppgåve 3 (4 poeng)
Punkta A (1,-1,0), B(3,1,1), og C(0,0,0) er gitt. a) Bestem . Bruk resultatet til å bestemme arealet av b) Bestem . Bruk mellom anna dette resultatet til å bestemme arealet avOppgåve 4 (3 poeng)
Løys differensiallikninga y' = 6xy når y(0) = 2Oppgåve 5 (5 poeng)
Ei rekkje er gitt ved a) Bestem og b) Forklar at rekkja er aritmetisk, og bruk dette til å finne eit uttrykk for og . c) Bestem kor mange ledd rekkja minst må ha for atOppgåve 6 (2 poeng)
Denne informasjonen er gitt om ein kontinuerleg funksjon f : • for alle • for alle • for x = -2 og for x = 2 • for x = 1 og for x = 3 Lag ei skisse som viser korleis grafen til f kan sjå ut.Oppgåve 7 (2 poeng)
Bruk induksjon til å bevise påstanden
Oppgåve 1 (4 poeng)
Ein pasient får 8 mL av ein medisin kvar time. Den totale mengda medisin i kroppen t timar etter at medisineringa starta, er y(t) mL. I løpet av ein time skil kroppen ut 5 % av den totale medisinmengda. a) Forklar at b) Vis at når y (0) = 0 c) Bestem . Kommenter svaret.Oppgåve 2 (6 poeng)
Funksjonen f er gitt ved a) Teikn grafen til f . b) Bestem eventuelle topp- og botnpunkt på grafen til f. c) Bestem arealet som er avgrensa av grafen til f og x-aksen.Oppgåve 3 (8 poeng)
Skissa nedanfor viser ein pyramide OABCD som er plassert i eit romkoordinatsystem. Hjørna i pyramiden er O(0,0,0) , A(3,0,0) , B(3,3,0) , C(0,3,0) og D(0,0,4)
a) Bestem ved rekning arealet av sideflata ABD i pyramiden.
b) Sideflata ABD ligg i eit plan ?.
Vis ved rekning at planet ? har likninga
4x + 3z - 12 = 0
c) Bestem avstanden frå punktet O til planet ?.
d) Bestem ved rekning vinkelen mellom dei to plana som sideflatene ABD og BCD ligg i.
Oppgåve 4 (6 poeng)
Figuren nedanfor viser ein sirkelsektor OBC der C ligg i første kvadrant. Bogen BC er ein del av sirkelen med likning . Punktet A har koordinatane (2,0) og
a) Vis at koordinatane til C er .
Bestem likninga for den rette linja gjennom O og C.
b) Når flatestykket blir dreidd 360° om x-aksen, får vi ei kjegle.
Bestem volumet av denne kjegla ved hjelp av integralrekning.
c) Når flatestykket blir dreidd 360° om x-aksen, får vi eit kulesegment.
Bestem volumet av dette kulesegmentet ved hjelp av integralrekning.
Oppgåve 5 (6 poeng)
På figuren er eit rektangel med sider x og y skrive inn i ein sirkel. Sirkelen har diameteren D. ?v er vinkelen mellom x og D.
a) Forklar at omkretsen O til rektangelet kan skrivast som
O(v) = 2Dcosv + 2Dsinv
Bestem eit funksjonsuttrykk for arealet A(v) av rektangelet.
b) Bruk O'(v) og vis at det rektangelet som har størst omkrets, er eit kvadrat.
Bestem den største omkretsen av rektangelet uttrykt ved diameteren D.
c) Bruk A'(v) og vis at det rektangelet som har størst areal, også er eit kvadrat.
Bestem det største arealet av rektangelet uttrykt ved diameteren D.
Oppgåve 6 (6 poeng)
Sierpi?ski-trekanten, som har fått namnet sitt etter den polske matematikaren Wac?aw Franciszek Sierpi?ski (1882–1969), lagar vi slik: 1. Vi startar med ein likesida, svart trekant har areal A. Sjå figur 1. 2. Midtpunktet på kvar av sidene i trekanten er hjørna i ein ny kvit, likesida trekant. Denne kvite trekanten fjernar vi. Vi står da igjen med tre likesida, svarte trekantar. Sjå figur 2. 3. Vi gjentek denne prosessen med kvar av dei svarte trekantane. Sjå figurane 3–5. Vi tenkjer oss at prosessen blir utført uendeleg mange gonger. Den «gjennomhola» figuren vi da står igjen med, blir kalla Sierpi?ski-trekanten.
Summen av areala som blir fjerna (dei kvite trekantane), er gitt ved rekkja
a) Bestem summen av rekkja ovanfor.
Kva fortel svaret ditt om arealet av Sierpi?ski-trekanten?
b) Sidene i trekanten i figur 1 er lik a.
Forklar at omkretsane av dei svarte trekantane i figurane 25? ovanfor er høvesvis
og
c) Vi gjer prosessen som forklart i trinn 2 ovanfor n gonger. Forklar at omkretsen av dei svarte trekantane da er lik
Forklar at når
Kva fortel det om omkretsen til Sierpi?ski-trekanten?
Gratis Prøvesmak
Superteknikker
En til en veiledning
Prøvesmak våre videoer
Mattevideo tilbyr fullstendig dekning av kursene 1P, 1PY, 1T, 2P, S1, R1, S2 og R2 innenfor videregående skole. Under har vi lagt ut noen smakebiter fra disse kursene, så du kan sjekke ut noe av det vi har å by på, før du bestemmer deg for å bli abonnent.1P - Polynomfunksjoner1PY - Prosentregning1T - Funksjonsbegrepet2P - Første gradS1 - LikningssettR1 - Å finn den deriverte ved å bruke derivasjonsreglerS2 - Aritmetiske og geometriske rekkerR2 - Sinusfunksjoner og cosinusfunksjoner
Lær å jobbe smarterepå 5 minutter
Det finnes mange ulike studieteknikker, utfordringen er ofte å finne de som fungerer best for deg. I oversikten under finner du enkelt de beste teknikkene.
Alle våre studietips er laget av vår superelev - med 6 i snitt fra vgs. Ingen av artiklene tar mer enn 5 minutter å lese - slik at du kan starte læringen så fort som mulig.
Hva skjer i hjernen når du lærer?
Du møter noe nytt for første gang
Du kobler den nye tingen med kunnskap du har fra før
Du repeter og styrker sammenhengene
Du bruker kunnskapen
Vanlige utfordringer - og hvordan løse dem
Teknikkene som gjør deg til en superelev
En til en veiledning
Ønsker du en uforpliktende samtale om dine behov?
La oss ringe deg, så finner vi en god løsning.
La oss ringe deg, så finner vi en god løsning.
06:43
Teori 2
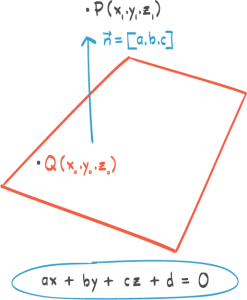
Avstand mellom parallelle linjer.
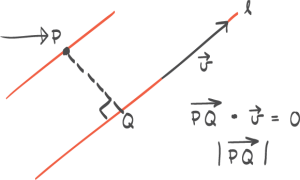
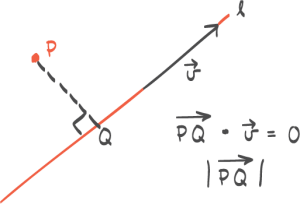
Når vi skal finne avstanden mellom to parallelle linjer kan vi gjøre noe av det vi gjorde da vi fant avstand fra et punkt til en linje. For vi kan egentlig bare fra den ene linja velge oss et punkt.
Quiz section 0
Hvordan kan man raskt finne avstand mellom to parallelle linjer?
Ved å velge et punkt og trekke normalen
Ved å gjette en vilkårlig avstand
Ved å tegne en trekant
Oppsummer det viktigste på 1-2-3,
klikk her for 10 sekunders quiz
klikk her for 10 sekunders quiz
Oppsummer det viktigste på 1-2-3
Og da er resten likt det vi har gjort tidligere, nemlig avstand fra punkt til den andre linja.
Quiz section 1
Kan tidligere metoder for avstand fra punkt til linje gjenbrukes ved parallelle linjer?
Ja, prinsippet er det samme
Nei, man må alltid utvikle en ny formel
Bare hvis linjene er identiske
Den teknikken gikk ut på at vi måtte gå normalt ned til den andre linjen, og der det normale treffer kan vi si at vi har et punkt q. Det punktet q gjør at p–q-vektoren står vinkelrett på retningsvektoren, hvor vi da skal ha et produkt lik null. Det låser egentlig hva p–q-vektoren blir, og når vi regner ut p–q til slutt, er det avstanden. Det høres enkelt ut, men det er fort gjort å gjøre feil. Vi kan si såpass mye som at dette ikke er første opptaket av denne videoen. Vi har prøvd et par ganger, og det er veldig fort gjort å gjøre en eller annen tullefeil. Her må man være veldig, veldig nøye.
Quiz section 2
Hvorfor er det viktig å bruke en normal i slike avstandsberegninger?
For at linjen skal bli lengre
For å unngå brøkregning
For at vektoren skal stå vinkelrett på linjen
Vi kan velge oss et punkt P. Da kan vi jo velge det her oppe, og hvis vi nå setter t lik null, så forsvinner t-leddene, og da har vi et punkt som heter én fem null.
Quiz section 3
Hvorfor kan man noen ganger velge en parameter lik null?
For å unngå at linjen blir parallell
For å hoppe over vektorer
For å forenkle punktvalget
Retningsvektoren kan vi ta hvor som helst, for disse linjene er parallelle.
Quiz section 4
Hvorfor er retningsvektoren ofte den samme for parallelle linjer?
Fordi linjer alltid er unike
Fordi man ønsker forskjellige normaler
Fordi parallelle linjer deler retning
Det ser vi, for de har faktisk samme retningsvektor, nemlig minus to, én, to.
Quiz section 5
Hva kjennetegner to linjer med samme retningsvektor?
De er parallelle
De er alltid sammenfallende
De er vinkelrett på hverandre
Sånn.
Quiz section 6
Hvorfor kan man velge et vilkårlig punkt på linja når de er parallelle?
Fordi avstanden er lik uansett punkt
Fordi retningsvektoren endrer seg
Fordi linjene krysser hverandre
Men så må vi ha punktet P, eller rettere sagt uttrykket for p–q-vektoren. Da kan vi si at siden vi har valgt punktet P her oppe, så ligger q på den nederste linja. Dermed er p–q koordinatene der nede minus koordinatene til P der oppe.
Quiz section 7
Hvorfor må man finne koordinatene til begge linjene?
For å få p–q-vektoren riktig
For å kunne lage store matriser
For å unngå å bruke normalvektor
Og da er p–q minus to t, og så trekker vi fra én, t minus fem, og tre pluss to t minus null. Null er ikke så mye å bry seg om, så da blir det bare sånn.
Quiz section 8
Hva betyr det at p–q-vektoren står vinkelrett på retningsvektoren?
At man må løse to ligninger
At avstanden blir uendelig
At skalarproduktet er null
Nå skal vi ha at produktet p–q ganget med vektoren v er lik null. Jeg tror jeg skriver v multiplisert med p–q, for det er jo det samme.
Quiz section 9
Hvorfor settes produktet (p–q) · v lik null i avstandsberegningen?
For å sikre at vektorene er vinkelrette
For å doble retningsvektoren
For å eliminere alle parametere
Da får vi altså minus to, én, to multiplisert med det som står der.
Quiz section 10
Hva betyr det å multiplisere to vektorer skalarielt?
Å få et tall som resultat
Å få en ny vektor
Å endre retningen til begge
Så må vi være litt effektive med tanke på plassen. Vi skal liksom bare fullføre på den tavleplassen her, så da må jeg være litt gjerrig med utregningene.
Quiz section 11
Hva er fordelen med å være effektiv i utregningene?
Man bruker mindre plass og tid
Man får flere parametere å velge mellom
Man unngår å lære nye metoder
Minus to multiplisert med «minus to t minus én» blir fire t pluss to. Én multiplisert med «t minus fem» gir oss t minus fem. Og to multiplisert med «tre pluss to t» blir seks pluss fire t. Dette skal være lik null.
Quiz section 12
Hvorfor kan man lett gjøre feil i slike beregninger?
Det finnes ingen universell metode
Fordi formler alltid er upålitelige
Små feil i tallbehandling gir store utslag
Hvor mange t-er har vi? Fire t pluss t og fire t til, det blir ni t. Så har vi to pluss «minus fem» pluss seks, som totalt gir tre. Flytter vi tre over på den andre siden, blir det minus tre. Det betyr at t er lik minus en tredjedel. Jeg synes det er greit.
Quiz section 13
Hvorfor samles termer med t i én likning?
For å finne riktig t-verdi i én beregning
For å unngå bruk av vektorer
For å få avstand lik null
Så må vi være litt nøye med dette. Vi har sjekket at det skal stemme. Da blir p–q …
Quiz section 14
Hvorfor er det lurt å dobbeltsjekke t-verdien man får?
For å finne en ny retningsvektor
For å se om linjene krysser hverandre
For å unngå feil i p–q-vektoren
Så må vi være litt …
Quiz section 15
Hvorfor oppstår det en ligning når vi krever at (p–q) er vinkelrett på v?
Fordi parametrene blir overflødige
Fordi man får en konstant verdi
Fordi skalarproduktet må være null
… effektive. Legg merke til at vi fikk null fordi vi brukte kravet her oppe. Det er det som gir oss ligningen.
Quiz section 16
Hvorfor nevnes presisjon og nøyaktighet ofte i slike oppgaver?
Det finnes ingen presise utregninger
Man kan bruke alle feil til sin fordel
Små glipp kan gi gale svar
Når vi nå skal finne p–q-vektoren, må vi sette inn riktig t-verdi i uttrykket. Da blir det minus to multiplisert med t, altså minus to multiplisert med minus en tredjedel, og så trekker vi fra én. Videre har vi t minus fem, hvor t er minus en tredjedel, og så tre pluss to t.
Quiz section 17
Hvorfor setter man inn t-verdien tilbake i uttrykket for p–q?
For å unngå parametre i retningsvektoren
For å fjerne alle tall
For å få de endelige koordinatene til vektoren
Og det må vi passe på å regne riktig ut.
Quiz section 18
Hvorfor er brøkregning ofte nødvendig?
Fordi parametere kan ha rasjonelle verdier
For å kunne bruke kalkulator raskere
For å erstatte normalvektoren helt
Hvis vi tar minus to multiplisert med minus en tredjedel, får vi to tredjedeler. Så trekker vi fra én (som er det samme som tre tredjedeler), og da blir nettoen minus én tredjedel.
Quiz section 19
Hvorfor må man være nøyaktig når man konverterer desimaltall til brøker?
Man får alltid integer-verdier
Man trenger ikke konvertere noe som helst
Små avrundingfeil kan endre svaret
Og så har vi to.
Quiz section 20
Hva skjer når vi kvadrerer negative brøkverdier?
De blir alltid null
De blir positive ved kvadrering
Brøker kan ikke kvadreres
Da tar vi «minus en tredjedel minus fem», og fem er femten tredjedeler, så vi ender opp med minus seksten tredjedeler. Deretter tar vi «tre pluss to multiplisert med minus en tredjedel». Det er tre pluss «minus to tredjedeler», som blir ni tredjedeler minus to tredjedeler, altså sju tredjedeler.
Quiz section 21
Hvorfor kan man ende opp med negative tall i koordinater?
Man har brukt feil retningsvektor
Parametrene kan gi slike verdier
Det er umulig å få negative tall
Men vi har sjekket dette her, og det skal stemme. Da blir p–q …
Quiz section 22
Hvorfor må man fortsatt kontrollere at skalarproduktet er null i etterkant?
For å bekrefte at vektorene er vinkelrette
For å gjøre om negative tall til positive
For å unngå å regne med lengde
Legg merke til at vi fikk null fordi vi brukte det kravet over.
Quiz section 23
Hvorfor minner denne metoden om andre geometriske beregninger?
Den bruker samme vinkelrette prinsipp
Den unngår alle bruk av koordinater
Den gir alltid svar lik null
For det er det som gjør at vi fikk en ligning.
Quiz section 24
Hvorfor gir kravet om null skalarprodukt en ligning?
Fordi kun én verdi av t oppfyller betingelsen
Fordi alle verdier av t blir like
Fordi retningsvektoren forsvinner
Og så blir p–q-vektoren: minus to t minus to, og t-verdien er minus en tredjedel. Sett inn riktig verdi i uttrykket.
Quiz section 25
Hva er hovedpoenget med å sette inn korrekt t-verdi?
Å unngå å beregne lengder
Å gjøre ligninger mer kompliserte
Å få riktig p–q-vektor
Minus én.
Quiz section 26
Hvorfor kan negative faktorer i t gi positive brøkresultater?
Brøker kan aldri bli positive
Negative faktorer blir automatisk null
Multiplikasjon med minus gir fort endring i fortegn
Og så skulle vi ta ti minus fem. Da blir det minus én tredjedel.
Quiz section 27
Hvorfor bør man dobbeltsjekke et tall som “fem” i slike formler?
Fordi fem ofte må konverteres til tredjedeler
Fordi fem ikke kan brukes i matematikk
Fordi fem er alltid negativt
Minus fem.
Quiz section 28
Hvorfor legger man sammen uttrykk som 3 pluss (minus 2/3)?
For å kombinere hele tall med brøkdeler
For å oppnå null
For å slette brøken helt
Og så skal vi ta tre pluss to t.
Quiz section 29
Hvorfor kan vi ikke unngå brøk når parameteren er negativ?
Fordi brøker oppstår naturlig i løsningen
Fordi det ikke finnes en normalvektor
Fordi alt nullstilles
Til slutt. Ja vel, tre pluss to, det var det …
Quiz section 30
Hvorfor må man ofte gjøre hoderegning når plassen er begrenset?
For å kutte ut alle formler
For å unngå å få riktige svar
For å spare tid og plass
Som …
Quiz section 31
Hvorfor kvadrerer vi hver koordinat når vi finner en lengde?
For å lage nye parametere
For å følge Pythagoras’ setning
For å slippe brøker helt
Og nå er dette litt brøkregning. Nå går vi på R to, så nå må vi vise vei. Vi har dårlig med plass, så da tar vi litt hoderegning her.
Quiz section 32
Hvorfor hender det at resultatet blir et desimaltall i stedet for en helhetlig brøk?
Fordi alt blir alltid heltall
Fordi brøk aldri kan brukes
Fordi vi gjerne avrunder i kalkulatoren
Minus to multiplisert med minus en tredjedel blir to tredjedeler. Så skal vi trekke fra én (tre tredjedeler), og da blir det minus én tredjedel.
Quiz section 33
Hvorfor kan det være nyttig å se på en faktor som 1/3 i alle ledd?
Det gjør alle tall større
Det kan forenkle kvadrering og summasjon
Det fjerner behovet for parametere
… og da ender vi på minus seksten tredjedeler.
Quiz section 34
Hvorfor legger vi sammen kvadrerte komponenter?
For å få summen i Pythagoras’ formel
For å øke lengden kunstig
For å kansellere brøker
Og så skal vi ta tre og så skal vi plusse på minus to tredjedeler. Tiden to ganger minus en tredjedel er jo minus to tredjedeler, ni tredjedeler minus to tredjedeler blir sju tredjedeler.
Quiz section 35
Hvorfor ender man ofte med et ikke-helt desimaltall som svar?
Fordi kvadratrøtter sjelden blir hele tall
Fordi man ikke brukte normalavstand
Fordi man ikke kan legge sammen to tall
Minus to tredjedeler, da for t-en to ganger minus en tredjedel …
Quiz section 36
Hvorfor kan man få minus to tredjedeler i en utregning?
Minus-tegn brukes ikke i matematikk
Man har alltid regnefeil
Parametervalget kan gjøre noen ledd negative
Tredjedeler.
Quiz section 37
Hva betyr det at man regner i tredjedeler?
At man uttrykker tall som brøker med 3 i nevner
At man alltid får hele tall
At man bruker et sekstallssystem
Og det betyr at lengden p–q …
Quiz section 38
Hvorfor går vi over til å beregne lengden av p–q-vektoren?
For å få selve avstanden i tallform
For å redusere alle parametere til null
For å lage en ny retning
Er lik roten av alt det der.
Quiz section 39
Hvorfor tar vi kvadratroten av summen av kvadrerte komponenter?
Det er definisjonen av vektorens lengde
For å slette t-verdien
For å få et heltall
Hver av komponentene i annen, slik jeg gjør nå …
Quiz section 40
Hvorfor får man ofte et omtrentlig tall som resultat?
Man unngår å legge sammen komponentene
Avrunding i kvadratroten gir desimaltall
Man gjør aldri brøkregning
Og det blir, hvis vi tar det på kalkulator, faktisk omtrent fem komma åttetre.
Quiz section 41
Hvorfor kan man foretrekke en brøkfaktor foran hele uttrykket?
Det kan forenkle utregningen av hvert ledd
Det gir alltid et heltall
Man unngår alle multiplikasjoner
Det du kan gjøre her, bare som en liten ting som går an …
Quiz section 42
Hvorfor fører begge metodene likevel til samme endelige resultat?
De bruker helt forskjellige utregninger
Den ene gir alltid feil svar
De baserer seg på samme matematiske prinsipp
Det er at man kunne gjort det slik at man sa at det var det samme som en tredjedel, og så bare skriver vi «minus én» der, «minus seksten» der, og «sju» der. Så kunne man tatt at lengden p–q …
Quiz section 43
Hvorfor kan man si at metoden med tredjedelsfaktor er lik den vanlige?
Fordi man endrer alle geometriske prinsipper
Fordi man ikke lenger trenger normalavstand
Fordi bare en faktor er trukket utenfor
Var lik en tredjedel av roten av en eller annen pluss seksten et eller annet pluss sju opphøyd i to. Legg merke til at den minus én forsvinner når du kvadrerer. Men det gir samme resultat, omtrent fem komma åttetre.
Quiz section 44
Hva er den typiske sluttverdien når man regner avstanden mellom parallelle linjer?
Et positivt tall som ofte er en desimal
Alltid null
Et tilfeldig negativt tall
Quiz section 45
Quiz section 46
Flott opplegg og undervisning😊
Tusen takk!
Gjorde unna R2 som privatist på et halvt år!! Mattevideo har gjort det mye lettere å fordøye et så tungt pensum på så kort tid. Tusen takk for hjelpa!!😊
Bra undervisning!
Jeg er fornøyd med videone deres det har hjulpet meg til å bestå matten i både Vgs og Uni . Så takk😊
Meget bra!
Tusen takk. Veldig flink lærer. Gode forklaringer.
Helt topp :D
Bra side.
Kjempebra!😊
Bra side. Veldig gode forklaringer😊
Tror dette kommer til å redde meg på noen prøver fremover. Takk! :D
takk for hjelpen
Takk for læreren av denne siden. Det er utrolig en bra side, fikk meg mye. Tusen hjertelig takk
Kan trygt anbefale Arne Hovland! Beste læreren jeg har hatt i løpet av drøyt 20 år med utdanning.
takk for denne siden :D min 1T mattelærer snakker så monotont og gjør matte så kjedelig at interessen svinner vekk og jeg sovner etter 5 minutter.