VGS matematikk
1 - 2 - 3 klasse
1 - 2 - 3 klasse
Lær VGS matten fra A til Å
med de beste metodene
Enkelt å
holde fokus
Forstå det
vanskelige
Få god
oversikt
Øv på
riktig tema
Få hjelp når
du stopper opp
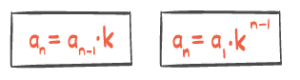
Følger og rekker
07:59
21:40
10:59
28:08
36:09
43:52
20:59
28:33
28:45
49:28
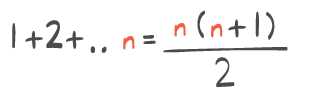
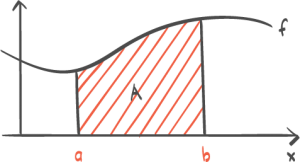
Integralregning
07:38
08:24
01:11
07:52
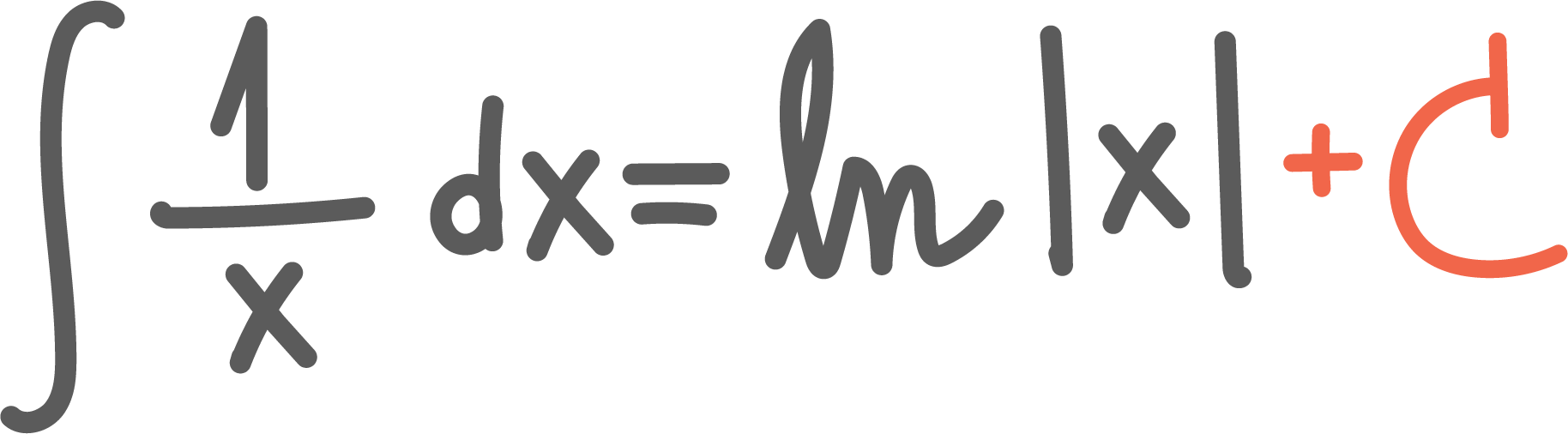
30:41
10:26
04:27
34:04
28:47
13:11
20:05
Integrasjonsmetoder
15:05
09:24
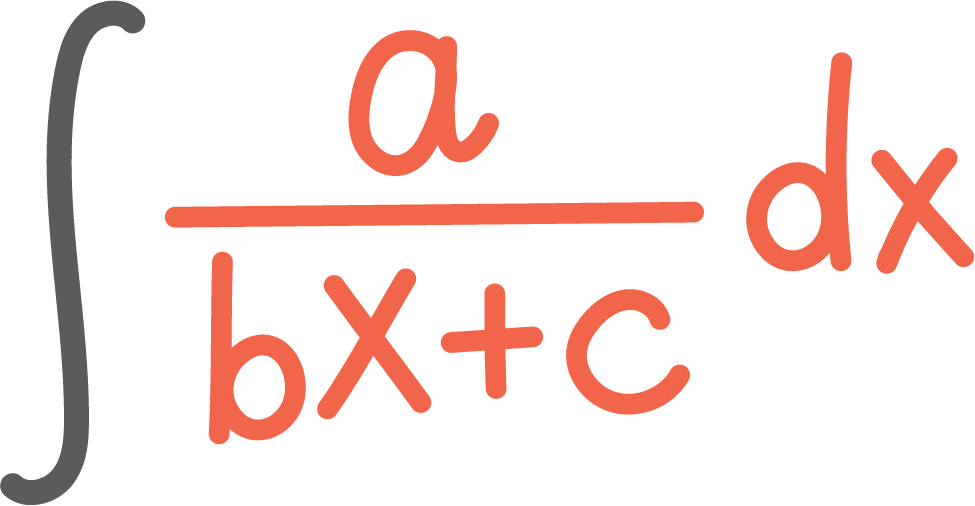
21:10
08:40
16:57
09:55
23:29
27:42
07:34
07:31
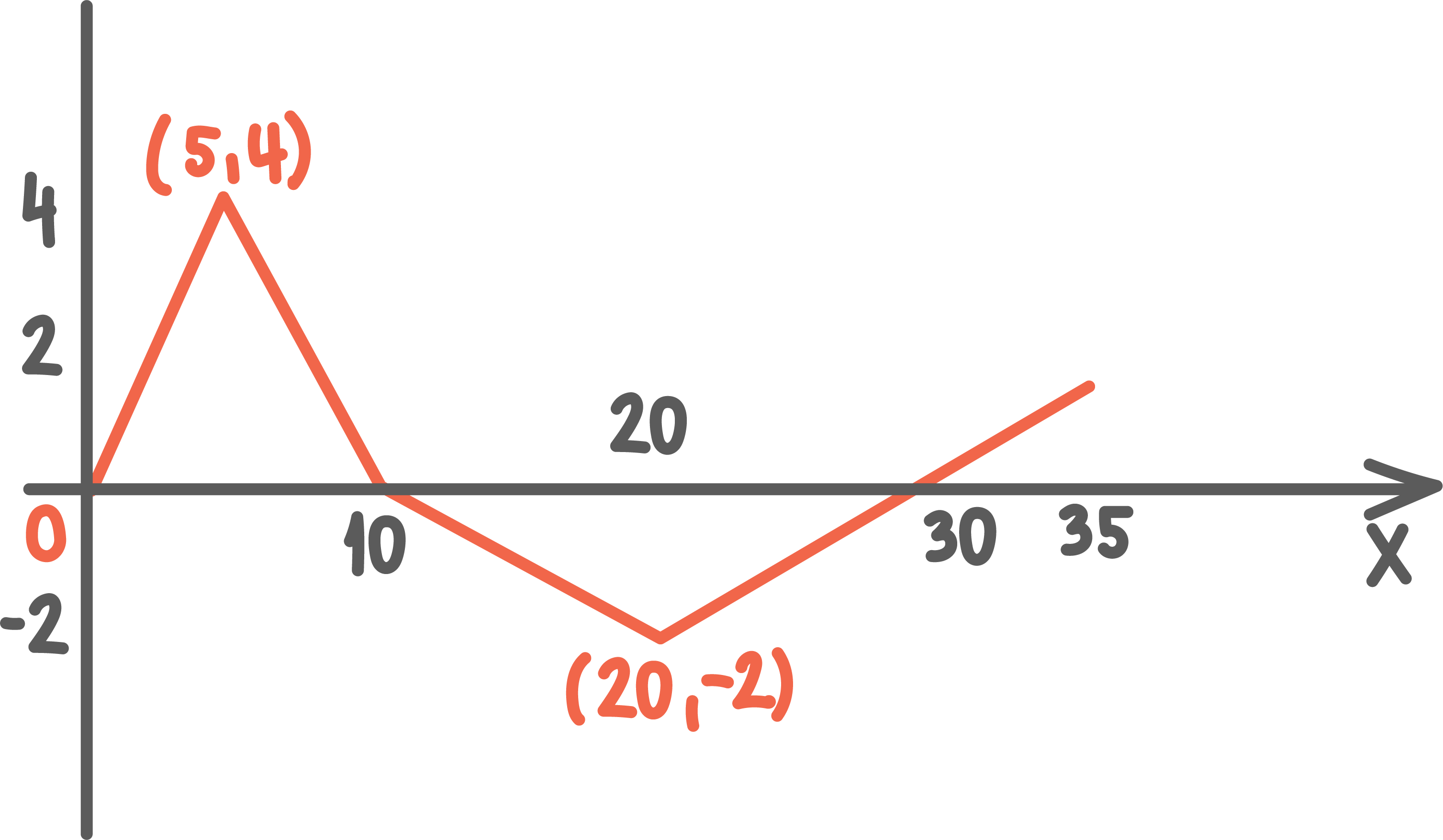
Vektorer
02:35
03:31
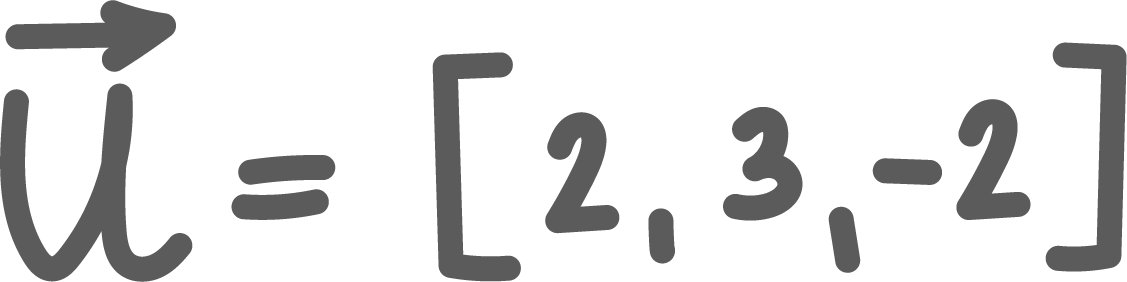
07:57
03:14
41:39
15:07
17:35
34:30
14:04
12:49
59:28
30:16
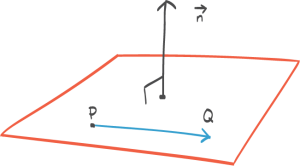
37:45
11:48
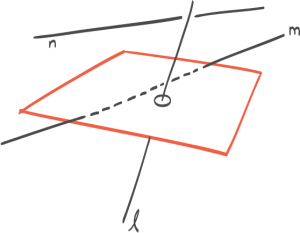
27:40
16:06
Trigonometri
19:21
08:45
21:24
03:26
13:21
09:44
03:30
11:22
03:06
15:54
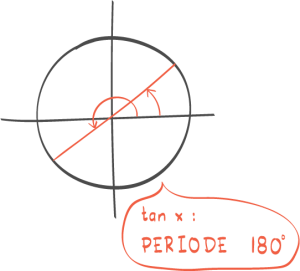
19:22
17:23
Funksjoner og kurver
13:18
05:28
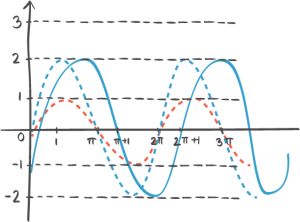
39:37
13:44
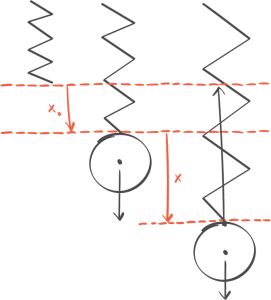
07:04
14:29
04:15
Eksamenstid 5 timer
Del 1 (Uten hjelpemidler) skal leveres etter 2 timer.
Del 2 (Med hjelpemidler) skal leveres etter senest 5 timer.
Oppgåve 1 (4 poeng)
Deriver funksjonane a) b) c)Oppgåve 2 (4 poeng)
Bestem integralet ved å bruke a) variabelskifte b) delbrøkoppspaltingOppgåve 3 (4 poeng)
Punkta A (1,-1,0), B(3,1,1), og C(0,0,0) er gitt. a) Bestem . Bruk resultatet til å bestemme arealet av b) Bestem . Bruk mellom anna dette resultatet til å bestemme arealet avOppgåve 4 (3 poeng)
Løys differensiallikninga y' = 6xy når y(0) = 2Oppgåve 5 (5 poeng)
Ei rekkje er gitt ved a) Bestem og b) Forklar at rekkja er aritmetisk, og bruk dette til å finne eit uttrykk for og . c) Bestem kor mange ledd rekkja minst må ha for atOppgåve 6 (2 poeng)
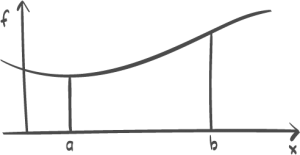
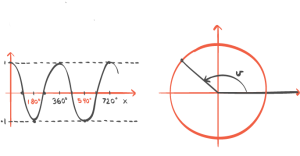
Denne informasjonen er gitt om ein kontinuerleg funksjon f : • for alle • for alle • for x = -2 og for x = 2 • for x = 1 og for x = 3 Lag ei skisse som viser korleis grafen til f kan sjå ut.Oppgåve 7 (2 poeng)
Bruk induksjon til å bevise påstanden
Oppgåve 1 (4 poeng)
Ein pasient får 8 mL av ein medisin kvar time. Den totale mengda medisin i kroppen t timar etter at medisineringa starta, er y(t) mL. I løpet av ein time skil kroppen ut 5 % av den totale medisinmengda. a) Forklar at b) Vis at når y (0) = 0 c) Bestem . Kommenter svaret.Oppgåve 2 (6 poeng)
Funksjonen f er gitt ved a) Teikn grafen til f . b) Bestem eventuelle topp- og botnpunkt på grafen til f. c) Bestem arealet som er avgrensa av grafen til f og x-aksen.Oppgåve 3 (8 poeng)
Skissa nedanfor viser ein pyramide OABCD som er plassert i eit romkoordinatsystem. Hjørna i pyramiden er O(0,0,0) , A(3,0,0) , B(3,3,0) , C(0,3,0) og D(0,0,4)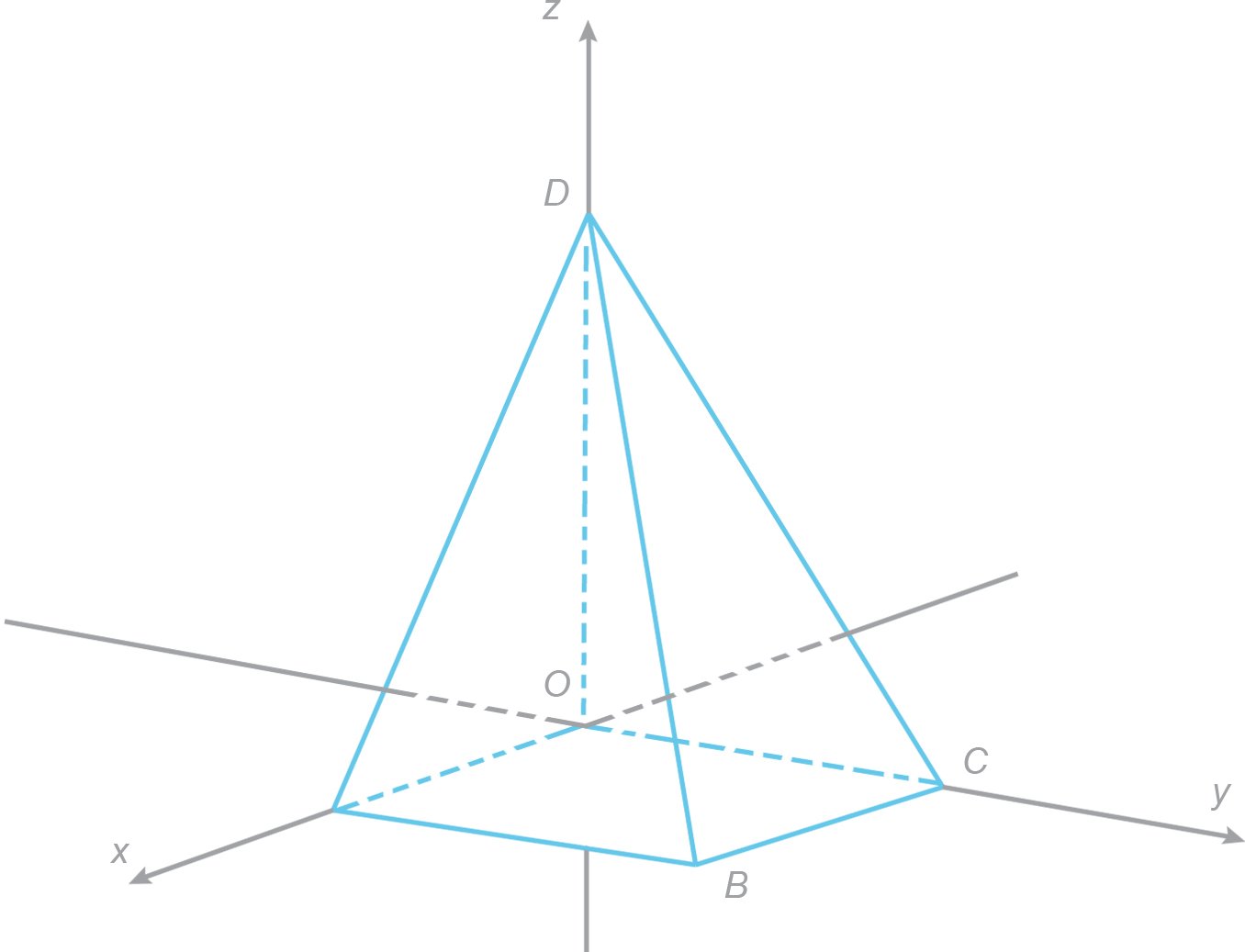
a) Bestem ved rekning arealet av sideflata ABD i pyramiden.
b) Sideflata ABD ligg i eit plan ?.
Vis ved rekning at planet ? har likninga
4x + 3z - 12 = 0
c) Bestem avstanden frå punktet O til planet ?.
d) Bestem ved rekning vinkelen mellom dei to plana som sideflatene ABD og BCD ligg i.
Oppgåve 4 (6 poeng)
Figuren nedanfor viser ein sirkelsektor OBC der C ligg i første kvadrant. Bogen BC er ein del av sirkelen med likning . Punktet A har koordinatane (2,0) og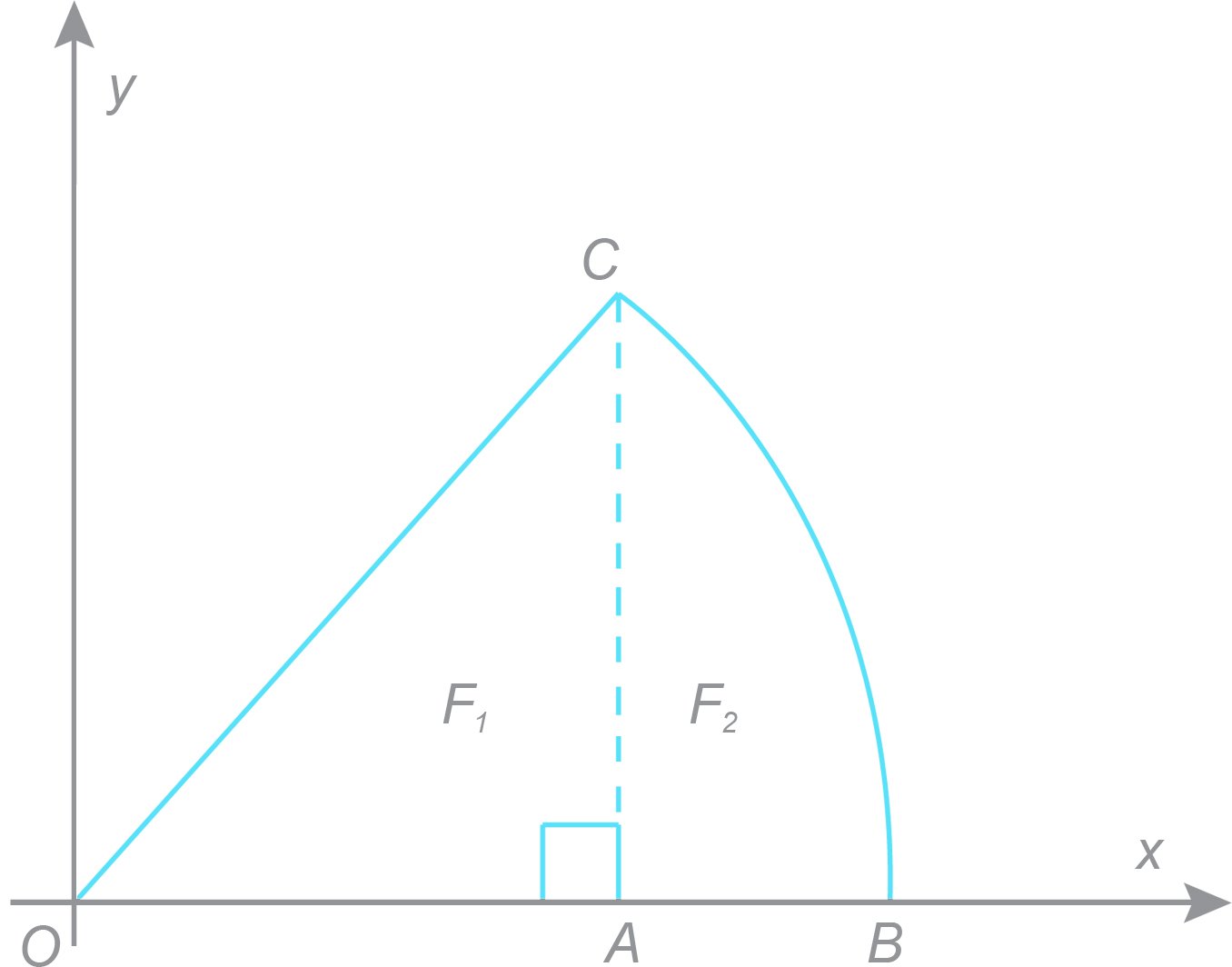
a) Vis at koordinatane til C er .
Bestem likninga for den rette linja gjennom O og C.
b) Når flatestykket blir dreidd 360° om x-aksen, får vi ei kjegle.
Bestem volumet av denne kjegla ved hjelp av integralrekning.
c) Når flatestykket blir dreidd 360° om x-aksen, får vi eit kulesegment.
Bestem volumet av dette kulesegmentet ved hjelp av integralrekning.
Oppgåve 5 (6 poeng)
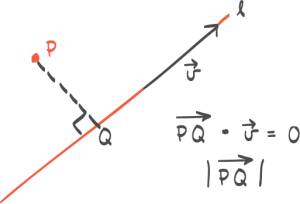
På figuren er eit rektangel med sider x og y skrive inn i ein sirkel. Sirkelen har diameteren D. ?v er vinkelen mellom x og D.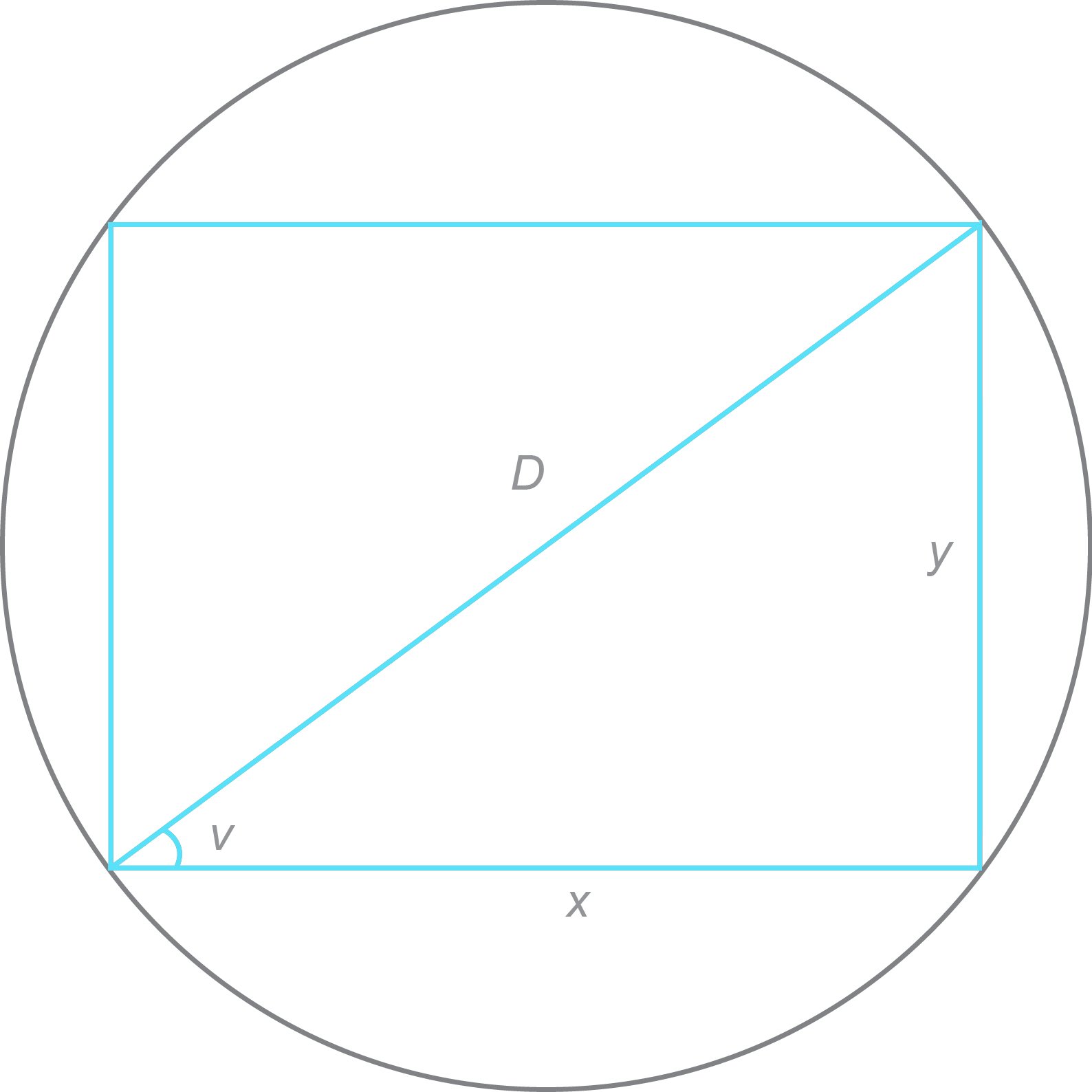
a) Forklar at omkretsen O til rektangelet kan skrivast som
O(v) = 2Dcosv + 2Dsinv
Bestem eit funksjonsuttrykk for arealet A(v) av rektangelet.
b) Bruk O'(v) og vis at det rektangelet som har størst omkrets, er eit kvadrat.
Bestem den største omkretsen av rektangelet uttrykt ved diameteren D.
c) Bruk A'(v) og vis at det rektangelet som har størst areal, også er eit kvadrat.
Bestem det største arealet av rektangelet uttrykt ved diameteren D.
Oppgåve 6 (6 poeng)
Sierpi?ski-trekanten, som har fått namnet sitt etter den polske matematikaren Wac?aw Franciszek Sierpi?ski (1882–1969), lagar vi slik: 1. Vi startar med ein likesida, svart trekant har areal A. Sjå figur 1. 2. Midtpunktet på kvar av sidene i trekanten er hjørna i ein ny kvit, likesida trekant. Denne kvite trekanten fjernar vi. Vi står da igjen med tre likesida, svarte trekantar. Sjå figur 2. 3. Vi gjentek denne prosessen med kvar av dei svarte trekantane. Sjå figurane 3–5. Vi tenkjer oss at prosessen blir utført uendeleg mange gonger. Den «gjennomhola» figuren vi da står igjen med, blir kalla Sierpi?s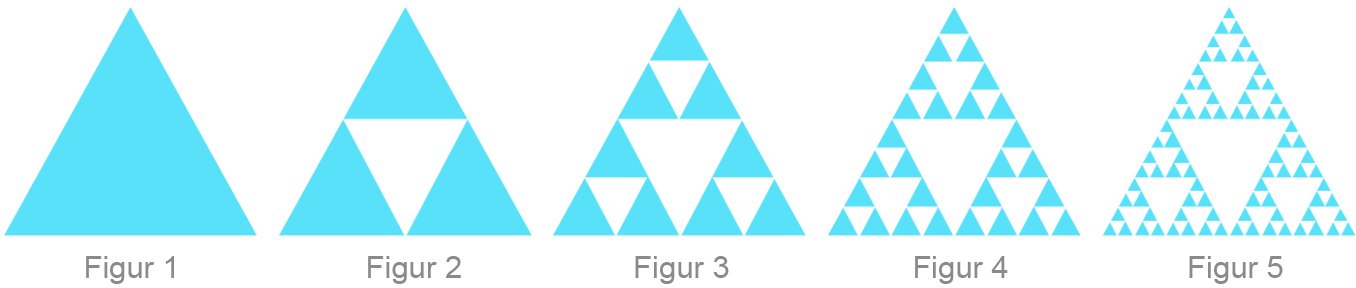ki-trekanten.
Summen av areala som blir fjerna (dei kvite trekantane), er gitt ved rekkja
a) Bestem summen av rekkja ovanfor.
Kva fortel svaret ditt om arealet av Sierpi?ski-trekanten?
b) Sidene i trekanten i figur 1 er lik a.
Forklar at omkretsane av dei svarte trekantane i figurane 25? ovanfor er høvesvis
og
c) Vi gjer prosessen som forklart i trinn 2 ovanfor n gonger. Forklar at omkretsen av dei svarte trekantane da er lik
Forklar at når
Kva fortel det om omkretsen til Sierpi?ski-trekanten?
Gratis Prøvesmak
Superteknikker
En til en veiledning
Prøvesmak våre videoer
Mattevideo tilbyr fullstendig dekning av kursene 1P, 1PY, 1T, 2P, S1, R1, S2 og R2 innenfor videregående skole. Under har vi lagt ut noen smakebiter fra disse kursene, så du kan sjekke ut noe av det vi har å by på, før du bestemmer deg for å bli abonnent.1P - Polynomfunksjoner1PY - Prosentregning1T - Funksjonsbegrepet2P - Første gradS1 - LikningssettR1 - Å finn den deriverte ved å bruke derivasjonsreglerS2 - Aritmetiske og geometriske rekkerR2 - Sinusfunksjoner og cosinusfunksjoner
Lær å jobbe smarterepå 5 minutter
Det finnes mange ulike studieteknikker, utfordringen er ofte å finne de som fungerer best for deg. I oversikten under finner du enkelt de beste teknikkene.
Alle våre studietips er laget av vår superelev - med 6 i snitt fra vgs. Ingen av artiklene tar mer enn 5 minutter å lese - slik at du kan starte læringen så fort som mulig.
Hva skjer i hjernen når du lærer?
Du møter noe nytt for første gang
Du kobler den nye tingen med kunnskap du har fra før
Du repeter og styrker sammenhengene
Du bruker kunnskapen
Vanlige utfordringer - og hvordan løse dem
Teknikkene som gjør deg til en superelev
En til en veiledning
Ønsker du en uforpliktende samtale om dine behov?
La oss ringe deg, så finner vi en god løsning.
La oss ringe deg, så finner vi en god løsning.
05:06
Teori 4
Og.. (cosx)' = -sinx
I denne videoen skal vi derivere cosinus X.
Quiz section 0
Hva betyr det å derivere en funksjon?
Å slette funksjonen fullstendig
Å finne funksjonens stigningstall
Å multiplisere funksjonen med x
Oppsummer det viktigste på 1-2-3,
klikk her for 10 sekunders quiz
klikk her for 10 sekunders quiz
Oppsummer det viktigste på 1-2-3
Og da skal vi få minus sinus X, og det er også en sånn regel som vi skal ta med oss videre.
Quiz section 1
Hva kan et negativt fortegn i en derivasjon indikere?
At funksjonen er jevn
At funksjonen avtar
At funksjonen alltid øker
Nå skal vi se hvorfor.
Quiz section 2
Hvorfor er bevis viktig i matematikk?
For å sikre at påstander er korrekte
For å unngå bruk av ligninger
For å gjøre oppgaver mer kompliserte
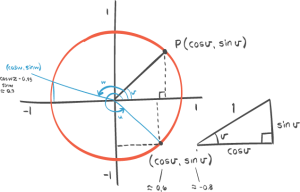
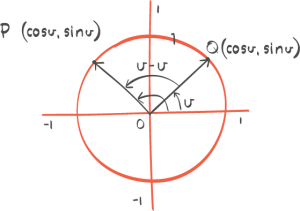
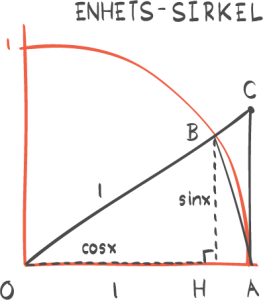
Cosinus X er nemlig det samme som sinus til nitti grader minus X, eller pi halve minus X, og det kan vi jo se på den trekanten der. Her har vi en sirkel, så dette kan gjelde alle vinkler, men vi holder oss bare i en sånn trekant nede med nitti grader der.
Quiz section 3
Hvilken sammenheng har sinus og cosinus for komplementære vinkler?
De er like
De utelukker hverandre
De er uavhengige av hverandre
Hvis den vinkelen heter X.
Quiz section 4
Kan en vinkel kalles X i matematikk?
Ja, vi kan bruke hvilken som helst bokstav
Nei, bare greske bokstaver er tillatt
Kun hvis X er mindre enn 90 grader
Og det er nitti der, så må det være nitti minus X der oppe, for hvis ikke blir det ikke ett hundre og åtti grader til sammen. Og hvis vi nå er i radianer i stedet, så er den vinkelen pi halve, og da blir den vinkelen pi halve minus X. Og cosinus i en vinkel.
Quiz section 5
Hvor mange grader utgjør vinkelsummen i en trekant?
180
90
360
Det er forholdet mellom den siden og den siden.
Quiz section 6
Hva uttrykker en trigonometrisk funksjon i en rettvinklet trekant?
Summen av alle vinklene
Forholdet mellom to sider
Arealet til trekanten
Men det forholdet er jo det samme som sinus til den vinkelen der oppe.
Quiz section 7
Hvilken side er motstående katet?
Siden ved den rette vinkelen
Den korteste siden i trekanten
Siden overfor vinkelen vi ser på
Altså må det gjelde det som står her.
Quiz section 8
Hva menes med en logisk konklusjon i matematikk?
Bare en gjetning
En deduksjon basert på forutgående steg
Et utsagn uten grunnlag
Fordi sinus til den vinkelen der oppe er motstående katet, som er den, delt på hypotenusen. Ja, så det blir det samme. Det vil si at når vi skal derivere cosinus X.
Quiz section 9
Hva er formelen for sinus i en rettvinklet trekant?
Hosliggende delt på hypotenusen
Motstående delt på hypotenusen
Hypotenusen delt på motstående
Så, for øyeblikket mangler vi et verktøy for å derivere cosinus X, men vi har lært oss en derivasjonsregel for sinus. Og da kan vi jo heller derivere.
Quiz section 10
Hvorfor er det nyttig å ha derivasjonsregler?
De gjør utregning umulig
De forenkler og systematiserer prosessen
De erstatter alle andre matematiske verktøy
Det som står der.
Quiz section 11
Kan man bruke tidligere resultater for å løse nye problemer?
Kun i avansert statistikk
Ja, det er et vanlig prinsipp i matematikk
Nei, hvert problem er unikt
Og da deriverer vi den i stedet.
Quiz section 12
Finnes det flere måter å derivere en funksjon på?
Det avhenger av funksjonens dimensjon
Ja, ofte kan man velge ulike fremgangsmåter
Nei, bare én metode er gyldig
Og hvordan gjør vi det? Jo, da gjør vi følgende: For det første har vi lært at sinus, når vi deriverer sinus, da får vi cosinus. Sinus X derivert er lik cosinus X, så det betyr at den sinusfunksjonen derivert blir cosinus.
Quiz section 13
Hva er den deriverte av sinus?
Cosinus
En konstant lik 0
Tangens
Men så må vi huske at det er jo det samme argumentet fortsatt.
Quiz section 14
Hvorfor er det viktig å holde oversikt over argumentet i en funksjon?
Det spiller ingen rolle for beregningen
Fordi det avgjør hvordan vi deriverer
For at funksjonen skal bli konstant
Det er ikke ekstra pi halve minus X.
Quiz section 15
Er det alltid nødvendig å sjekke funksjonsargumentet før derivasjon?
Nei, argumentet er uviktig
Ja, det kan påvirke resultatet
Bare hvis funksjonen ikke er trigonometrisk
Og når det er litt mer kompliserte ting inni her enn bare X, da må vi huske å gange med kjernen derivert.
Quiz section 16
Hva kalles regelen for derivasjon av en funksjon inni en funksjon?
Produktregelen
Kjerneregelen
Den omvendte regelen
Og det betyr pi halve minus X.
Quiz section 17
Hva skjer med en konstant i en derivasjon?
Den endrer ikke verdi
Den blir 0
Den fordobles
Derivert.
Quiz section 18
Betyr «derivert» og «avledet» det samme i matematikk?
Nei, «avledet» betyr alltid multiplikasjon
Ja, de brukes om hverandre
De refererer til helt ulike prosesser
Og det blir...
Quiz section 19
Er mellomsteg noen ganger nødvendig i en utregning?
Bare hvis man ikke kan brøkregning
Aldri, man hopper rett til svaret
Ja, det kan gjøre prosessen tydeligere
Ja, jeg tror jeg tar det. Vi tar det under, det er lett å se da.
Quiz section 20
Kan det være lurt å notere steg underveis?
Ja, det gir bedre oversikt
Nei, det skaper bare rot
Kun i geometri
Når jeg har lyst til å vente litt med den, så deriverer vi den der borte med en gang, og det blir minus én.
Quiz section 21
Hva er den deriverte av −X?
1
−1
0
Så kunne jeg skrevet det der på nytt, men det som er det morsomme, er jo at det der er jo cosinus til pi halve minus X, er jo faktisk sinus.
Quiz section 22
Gjelder likheten cos(π/2 − v) = sin(v) for alle v?
Nei, bare for heltallige v
Ja, det er en generell identitet
Kun hvis v er under 90 grader
Til X.
Quiz section 23
Er X vanligvis en vinkel i trigonometrien?
Bare i geometri, aldri i trigonometrien
Nei, X angir alltid et tall over 10
Ja, X brukes ofte som et vinkelmål
Akkurat samme argumentet som vi tok i stad. Sinus til X, for å begynne med. Den vinkelen der, det er den siden, motstående [..], men det forholdet...
Quiz section 24
Er argumentet i en trigonometrisk funksjon ofte en vinkel?
Bare i avansert analyse
Nei, argumentet er alltid et heltall
Ja, det er vanlig
Den motstående kateten til den blir jo den hosliggende kateten til den vinkelen der oppe.
Quiz section 25
Hvilke sider brukes i definisjonen av cosinus i en rettvinklet trekant?
Motstående og hypotenusen
Hosliggende og hypotenusen
De to korteste sidene
Hosliggende delt på nytt. Det er jo cosinus til den vinkelen, altså det som står der. Så den er den samme som den.
Quiz section 26
Hva er den vanlige formelen for cosinus?
Hosliggende / hypotenuse
Motstående / hypotenuse
Hypotenuse / motstående
Og da står det jo...
Quiz section 27
Er det vanlig å forenkle uttrykk etter hvert steg?
Nei, man bruker kun sluttresultatet
Ja, for å se mønstre og feil lettere
Bare i numeriske metoder
Minus sinus.
Quiz section 28
Hva innebærer et negativt fortegn foran en trigonometrisk funksjon?
At funksjonen har en annen periode
At funksjonen speiles om x-aksen
At funksjonen ikke eksisterer
X og da er vi ferdig. Men la meg til slutt bare gjøre en ting: Det er jo noen som ikke er så gode venner med kjerneregelen, som jeg kanskje var nå. Så det er noen som liker å gjøre dette her. Skal vi se, hvis vi har sinus til...
Quiz section 29
Er det lurt å dobbeltsjekke resultater i matematikk?
Ja, for å forsikre seg om korrekthet
Nei, det fører ofte til feil
Bare i geometri
Pi halve minus X. Nå gidder jeg ikke bruke så masse farger når vi skal derivere den. Så er det noen som liker å si at det der blir...
Quiz section 30
Har fargebruk betydning for forståelse i matematiske utledninger?
Det er ikke tillatt i formelle bevis
Det er helt nødvendig for alle bevis
Det kan hjelpe, men er ikke avgjørende
At man skal ta sinus U derivert, og så skal man gange med U derivert etterpå.
Quiz section 31
Hvilken derivasjonsmetode brukes når funksjonen har en indre funksjon?
Kjerneregelen
Kvotientregelen
Grenseverdiregelen
Og da blir det...
Quiz section 32
Er det nyttig å forklare alle steg i en matematisk utledning?
Kun i muntlige presentasjoner
Nei, detaljene forvirrer
Ja, det gir bedre oversikt og færre feil
Cosinus U, og U deriverte var den greia der. Og den U, det er liksom pi halve.
Quiz section 33
Er detaljerte mellomregninger nyttige for å unngå feil?
Nei, man bør alltid hoppe rett til svaret
Ja, da ser man lettere eventuelle feilskjær
Bare hvis ligningen er lineær
Minus X, og U-derivert, det blir jo da minus én.
Quiz section 34
Hvorfor gir derivasjon av −X en negativ faktor?
Fordi vi alltid legger til en konstant
Fordi den deriverte av −X er −1
Fordi funksjonen blir multiplisert med X
Og så har vi akkurat den samme greia. Når vi da stopper inn U, så blir det cosinus.
Quiz section 35
Hvorfor er det viktig å erstatte U med det opprinnelige uttrykket?
Det er ikke nødvendig i noen tilfeller
For å få et endelig resultat i riktig form
Kun for å teste numeriske svar
Til pi halve minus X, og så ganger vi med minus én, og så bytter vi den over til sinus, som vi gjorde i stad.
Quiz section 36
Er substitusjon et vanlig verktøy i matematikk?
Nei, det brukes kun i statistikk
Ja, det er en sentral metode
Bare dersom man har brøkuttrykk
Og da står det minus sinus.
Quiz section 37
Kan sinus bli negativ?
Ja, avhengig av vinkelen
Nei, sinus er alltid positiv
Bare når vinkelen er 0
Men altså, jeg er ikke så veldig begeistret for å gjøre alt det der. Jeg synes på en måte man klarer å tenke at vi må huske at siden det er sinus til noe litt mer komplisert, så holder det ikke bare å derivere den. Man må også derivere det inni. Jeg foretrekker å ikke gjøre sånn som jeg gjorde der nede, men folk er forskjellige. Sånn kan man også gjøre det.
Quiz section 38
Finnes det flere gyldige måter å tilnærme seg et matematisk problem på?
Nei, bare én metode kan være riktig
Ja, ulike framgangsmåter kan gi samme svar
Metoden avhenger kun av språkvalg
Quiz section 39
Quiz section 40
11:54
Teori 1
Vi beviser at
05:04
Teori 2
Vi beviser at
09:54
Teori 3
Vi beviser at (sinx)' = cosx. Beviset bygger på setningene vi viste i teorivideo 1 og 2.
03:17
Teori 5
Vi deriverer .
02:19
Teori 6
Derivasjon og integrasjon av trigonemtriske funksjoner - reglene.
03:56
Teori 7
Antiderivasjonsregler - basisreglene.
14:20
Oppgave 1
t timer etter midnatt er temperaturen i et lagerrom gitt ved
a) Når er temperaturen høyest, og hvor mange grader er det da?
b) Når er temperaturen lavest, og hvor mange grader er det da?
c) Hva er gjennomsnittstemperaturen?
00:48
Oppgave 2
Finn f'(x) når f(x) = 3sinx - 2
01:34
Oppgave 3
Deriver funksjonen
01:45
Oppgave 4
Deriver funksjonen
02:23
Oppgave 5
Er det riktig at ?
06:20
Oppgave 6
Et sted ved sjøen er variasjonen i vanndybden i løpet av et døgn gitt ved funksjonen , der t er tiden målt i timer fra midnatt, og f er dybden målt i meter.
a) Hva er vanndybden kl 6 om morgenen?
b) Forklar hvorfor den største vanndybden blir 5,1 meter.
c) Hva blir den minste vanndybden?
d) Hva er perioden til funksjonen f ?
06:42
Oppgave 7
Gitt funksjonen
a) Finn f'(x) og eventuelle topp- eller bunnpunkter.
a) Finn f'(x) og eventuelle topp- eller bunnpunkter.
12:06
Oppgave 8
Gitt funksjonen
b) Finn f''(x) og eventuelle vendepunkter.
b) Finn f''(x) og eventuelle vendepunkter.
03:13
Oppgave 9
Gitt funksjonen
c) Tegn grafen til f .
c) Tegn grafen til f .
02:45
Oppgave 10
Regn ut
03:54
Oppgave 11
Regn ut
08:36
Oppgave 12
Et rektangel er innskrevet i den øvre halvdelen av en enhetssirkel, som vist i figuren i videoen.
a) Vis at arealet av rektangelet kan uttrykkes der .
b) Uten å bruke derivajon:
1) For hvilken vinkel er arealet av rektangelet størst.
2) Hvor stort er da arealet.
c) Vis på to måter at .
d) Bekreft svarene i b) ved bruke den deriverte.
03:14
Oppgave 13
Gitt funksjonen . Finn arealet avgrenset av grafen til f, y-aksen, og den positive delen av x-aksen.
Flott opplegg og undervisning😊
Tusen takk!
Gjorde unna R2 som privatist på et halvt år!! Mattevideo har gjort det mye lettere å fordøye et så tungt pensum på så kort tid. Tusen takk for hjelpa!!😊
Bra undervisning!
Jeg er fornøyd med videone deres det har hjulpet meg til å bestå matten i både Vgs og Uni . Så takk😊
Meget bra!
Tusen takk. Veldig flink lærer. Gode forklaringer.
Helt topp :D
Bra side.
Kjempebra!😊
Bra side. Veldig gode forklaringer😊
Tror dette kommer til å redde meg på noen prøver fremover. Takk! :D
takk for hjelpen
Takk for læreren av denne siden. Det er utrolig en bra side, fikk meg mye. Tusen hjertelig takk
Kan trygt anbefale Arne Hovland! Beste læreren jeg har hatt i løpet av drøyt 20 år med utdanning.
takk for denne siden :D min 1T mattelærer snakker så monotont og gjør matte så kjedelig at interessen svinner vekk og jeg sovner etter 5 minutter.