
1 - 2 - 3 klasse

Lær VGS matten fra A til Å
med de beste metodene


Enkelt å
holde fokus



Forstå det
vanskelige


Få god
oversikt


Øv på
riktig tema


Få hjelp når
du stopper opp








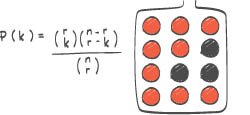


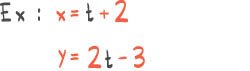
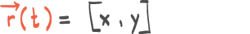
Oppgave 1 (5 poeng)
Deriver funksjonenea)
b)
c)
Oppgave 2 (4 poeng)
Skriv så enkelt som muliga)
b)
Oppgave 3 (4 poeng)
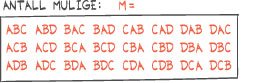
Tre punkt , og er gitt.a) Bestem og
Et punkt er gitt slik atb) Bestem koordinatene til
Oppgave 4 (6 poeng)
Funksjonen P er gitt veda) Begrunn at er et vendepunkt på grafen til . b) Faktoriser i lineære faktorer. c) Løs likningen
Oppgave 5 (6 poeng)
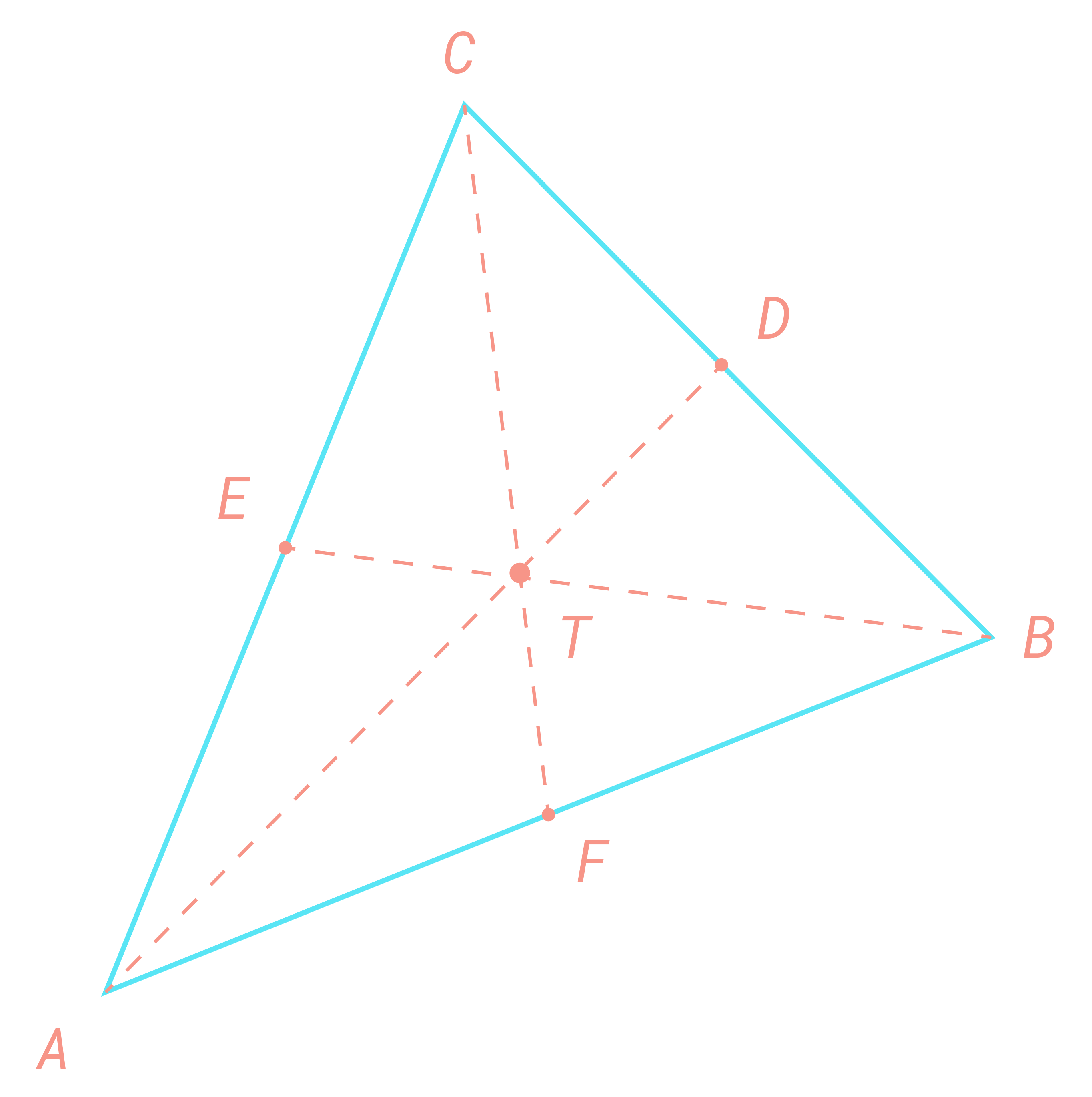
a) Forklar at koordinatene til punktene , og er
, og
Skjæringspunktet mellom medianene i trekanten er T.b) Forklar at vi kan skrive på to måter:
der s og t er reelle tall.
c) Bruk vektorlikningene i oppgave b) til å bestemme s og t. Bestem koordinatene til T.
Oppgave 6 (4 poeng)
En fabrikk produserer lyspærer. Alle lyspærene blir kontrollert. I kontrollen blir 8,0 % av lyspærene forkastet. Nærmere undersøkelser viser at- 92,0 % av de forkastede lyspærene er defekte
- 2,0 % av de godkjente lyspærene er defekte
Oppgave 7 (7 poeng)
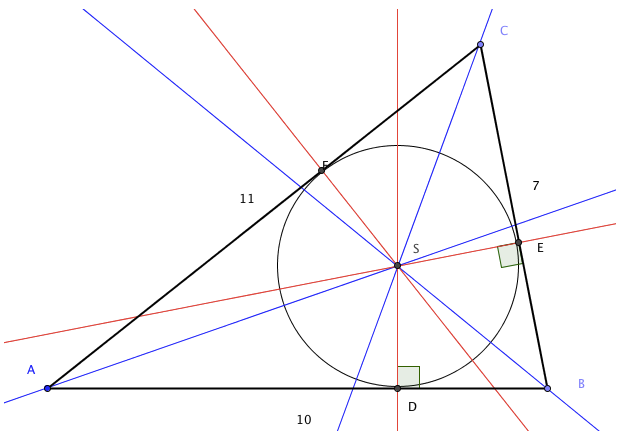
En rettvinklet der er gitt. Den innskrevne sirkelen har sentrum i og radius . Sirkelen tangerer trekanten i punktene , og . Vi setter , og . Du får oppgitt at og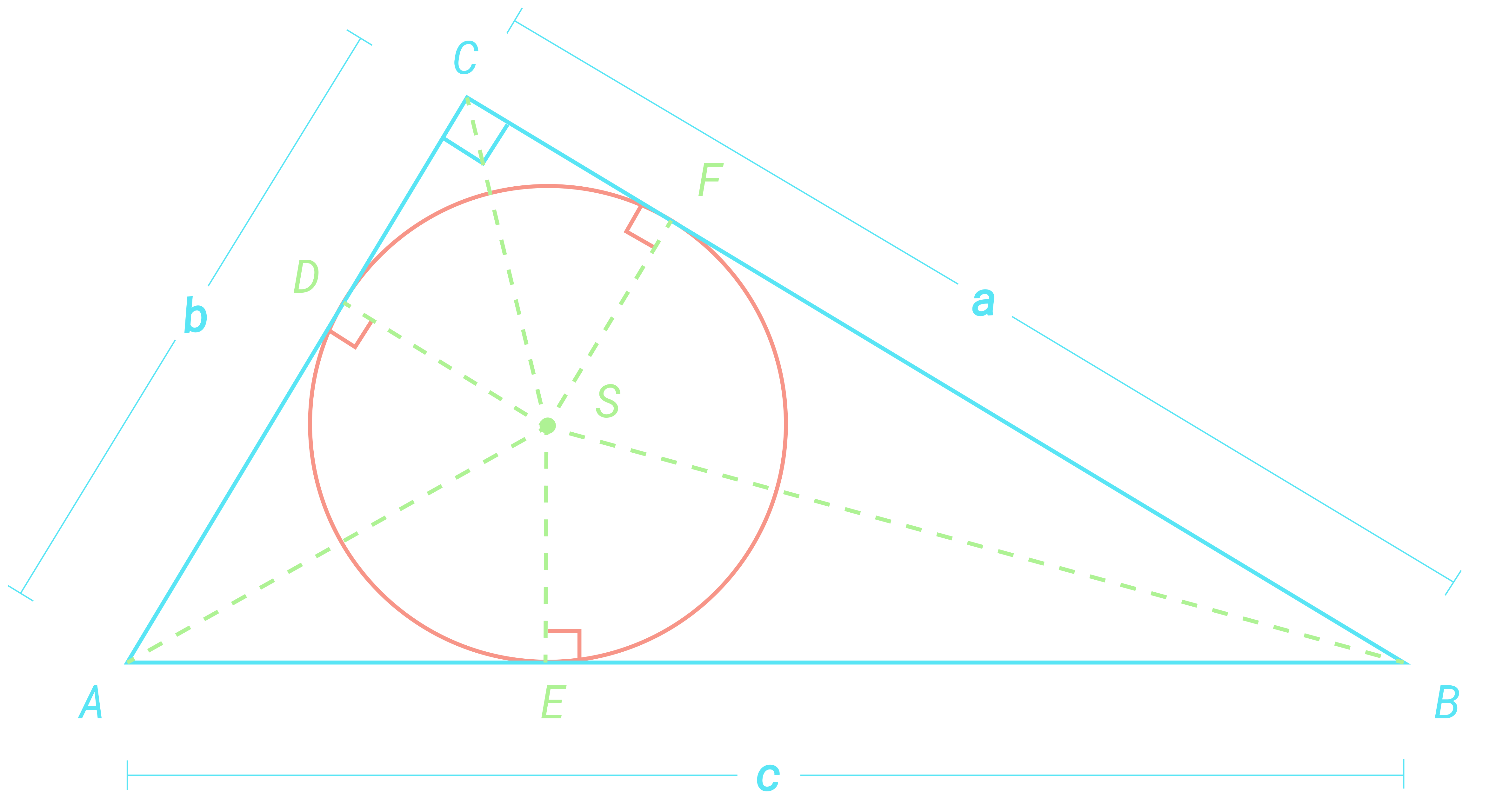
a) Bruk figuren til å forklare at og
Av figuren ser vi dessuten atb) Vis at
c) Forklare at vi kan skrive arealet T av trekanten på to måter:
og
d) Bruk resultatene du fant i oppgavene b) og c) til å utlede Pytagoras' setning.
Oppgave 1 (6 poeng)
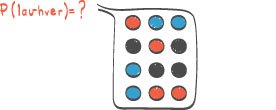
I en kortstokk er det 52 kort. Kortene er fordelt på de fire fargene hjerter, ruter, spar og kløver. Hver farge har 13 kort fordelt på verdiene 2 til 10, knekt, dame, konge og ess. Tenk deg at du skal trekke tilfeldig fem kort fra kortstokken.a) Bestem sannsynligheten for at du kommer til å trekke nøyaktig tre kort med verdi 10.
b) Bestem sannsynligheten for at du kommer til å trekke nøyaktig tre kort med samme verdi.
c) Bestem sannsynligheten for at alle kortene du kommer til å trekke, har samme farge.

Oppgave 2 (6 poeng)
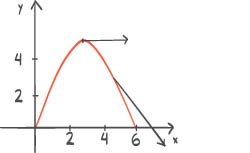
Posisjonsvektoren til en partikkel er gitt veda) Tegn grafen til når . b) Bestem fertsvektoren og akselerasjonsvektoren . c) Bruk CAS til å bestemme den minste banefarten til partikkelen.
Oppgave 3 (4 poeng)
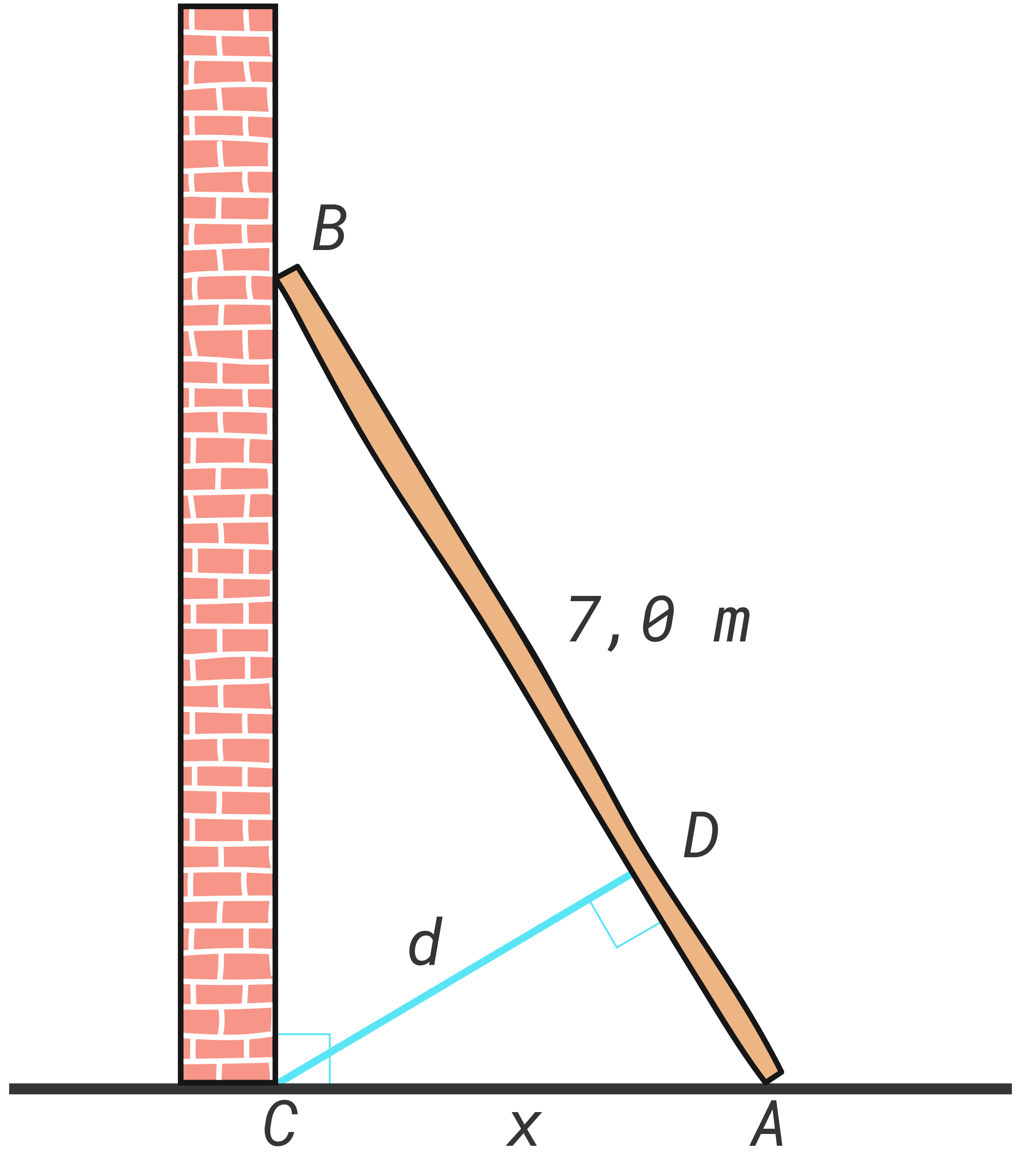
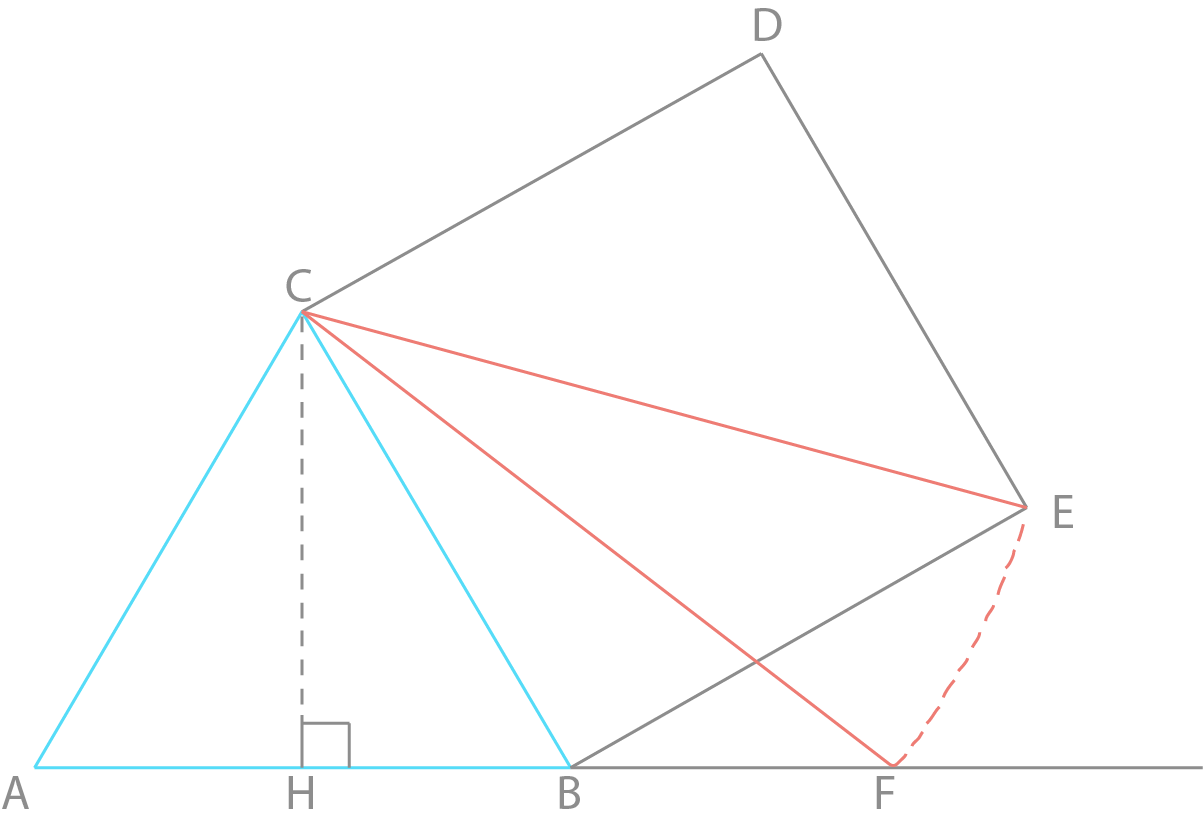
a) Vis at
b) Bestem slik at blir lengst mulig.
Hvor lang er d for denne verdien av x ?
Oppgave 4 (8 poeng)
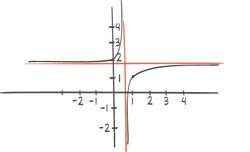
Funksjonen er gitt ved
a) Bruk graftegner til å tegne grafen til .
Grafen til har tre tangenter som går gjennom punktet .b) Forklar at x-koordinaten til tangeringspunktene må være løsning av likningen
c) Bruk CAS til å løse denne likningen. Bestem likningen til hver av tangentene.
La være et punkt i planet.d) Hva er det maksimale antallet tangenter grafen til kan ha som går gjennom ?
Prøvesmak våre videoer
Mattevideo tilbyr fullstendig dekning av kursene 1P, 1PY, 1T, 2P, S1, R1, S2 og R2 innenfor videregående skole. Under har vi lagt ut noen smakebiter fra disse kursene, så du kan sjekke ut noe av det vi har å by på, før du bestemmer deg for å bli abonnent.1P - Polynomfunksjoner1PY - Prosentregning1T - Funksjonsbegrepet2P - Første gradS1 - LikningssettR1 - Å finn den deriverte ved å bruke derivasjonsreglerS2 - Aritmetiske og geometriske rekkerR2 - Sinusfunksjoner og cosinusfunksjoner

Lær å jobbe smarterepå 5 minutter
Det finnes mange ulike studieteknikker, utfordringen er ofte å finne de som fungerer best for deg. I oversikten under finner du enkelt de beste teknikkene.
Alle våre studietips er laget av vår superelev - med 6 i snitt fra vgs. Ingen av artiklene tar mer enn 5 minutter å lese - slik at du kan starte læringen så fort som mulig.
Hva skjer i hjernen når du lærer?
 Du møter noe nytt for første gang
Du møter noe nytt for første gang Du kobler den nye tingen med kunnskap du har fra før
Du kobler den nye tingen med kunnskap du har fra før Du repeter og styrker sammenhengene
Du repeter og styrker sammenhengene Du bruker kunnskapen
Du bruker kunnskapen

Vanlige utfordringer - og hvordan løse dem


Teknikkene som gjør deg til en superelev
La oss ringe deg, så finner vi en god løsning.


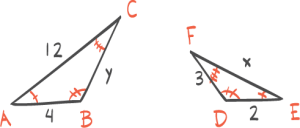


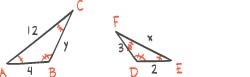
1) Tegn figur.
2) Forklar at trekant ACD og trekant BCD er kongruente.





























Flott opplegg og undervisning😊
Tusen takk!
Gjorde unna R2 som privatist på et halvt år!! Mattevideo har gjort det mye lettere å fordøye et så tungt pensum på så kort tid. Tusen takk for hjelpa!!😊
Bra undervisning!
Jeg er fornøyd med videone deres det har hjulpet meg til å bestå matten i både Vgs og Uni . Så takk😊
Meget bra!
Tusen takk. Veldig flink lærer. Gode forklaringer.
Helt topp :D
Bra side.
Kjempebra!😊
Bra side. Veldig gode forklaringer😊
Tror dette kommer til å redde meg på noen prøver fremover. Takk! :D
takk for hjelpen
Takk for læreren av denne siden. Det er utrolig en bra side, fikk meg mye. Tusen hjertelig takk
Kan trygt anbefale Arne Hovland! Beste læreren jeg har hatt i løpet av drøyt 20 år med utdanning.
takk for denne siden :D min 1T mattelærer snakker så monotont og gjør matte så kjedelig at interessen svinner vekk og jeg sovner etter 5 minutter.