
1 - 2 - 3 klasse

Lær VGS matten fra A til Å
med de beste metodene


Enkelt å
holde fokus



Forstå det
vanskelige


Få god
oversikt


Øv på
riktig tema


Få hjelp når
du stopper opp



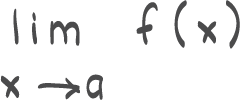



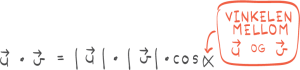
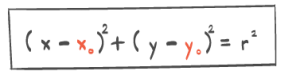
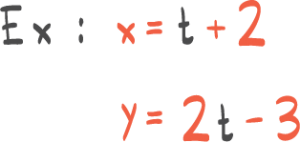
Se gjennom eksamen
Oppgave 1 (5 poeng)
Deriver funksjonenea) f(x)=2x3−5x+4
b) g(x)=x2ex
c) h(x)=x2−3
Oppgave 2 (4 poeng)
Skriv så enkelt som muliga) x2−9x2−3+x+31+x−35
b) 2⋅ln(a−3⋅b2) − 3⋅ln(a2b)
Oppgave 3 (4 poeng)
Tre punkt A(−1,6), B(2,1) og C(4,4) er gitt.a) Bestem AB og AC
Et punkt D er gitt slik atb) Bestem koordinatene til D
Oppgave 4 (6 poeng)
Funksjonen P er gitt vedP(x)=2x3−6x2−2x+6
a) Begrunn at (1,0) er et vendepunkt på grafen til P. b) Faktoriser P(x) i lineære faktorer. c) Løs likningen2e3x−6e2x−2ex+6=0
Oppgave 5 (6 poeng)
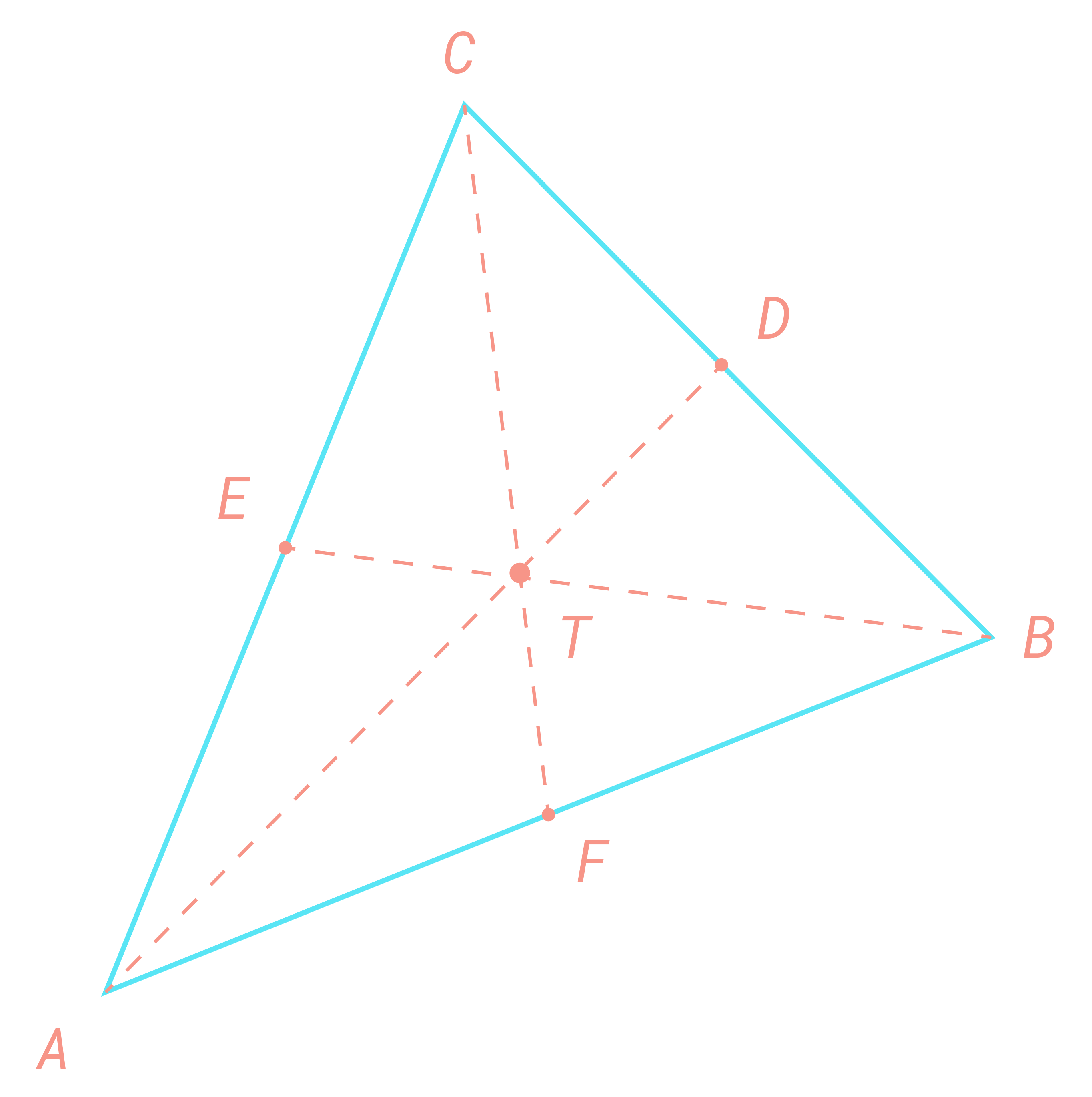
a) Forklar at koordinatene til punktene D, E og F er
D(29,27), E(2,25) og F(27,1)
Skjæringspunktet mellom medianene i trekanten er T.b) Forklar at vi kan skrive AT på to måter:
AT=s⋅AD , s=R
AT=AB+t⋅BE , t=R
der s og t er reelle tall.
c) Bruk vektorlikningene i oppgave b) til å bestemme s og t. Bestem koordinatene til T.
Oppgave 6 (4 poeng)
En fabrikk produserer lyspærer. Alle lyspærene blir kontrollert. I kontrollen blir 8,0 % av lyspærene forkastet. Nærmere undersøkelser viser at- 92,0 % av de forkastede lyspærene er defekte
- 2,0 % av de godkjente lyspærene er defekte
Oppgave 7 (7 poeng)
En rettvinklet ΔABC der ∠C=90o er gitt. Den innskrevne sirkelen har sentrum i S og radius r. Sirkelen tangerer trekanten i punktene D, E og F. Vi setter AC=b, BC=a og AB=c. Du får oppgitt at BF=BE og AD=AE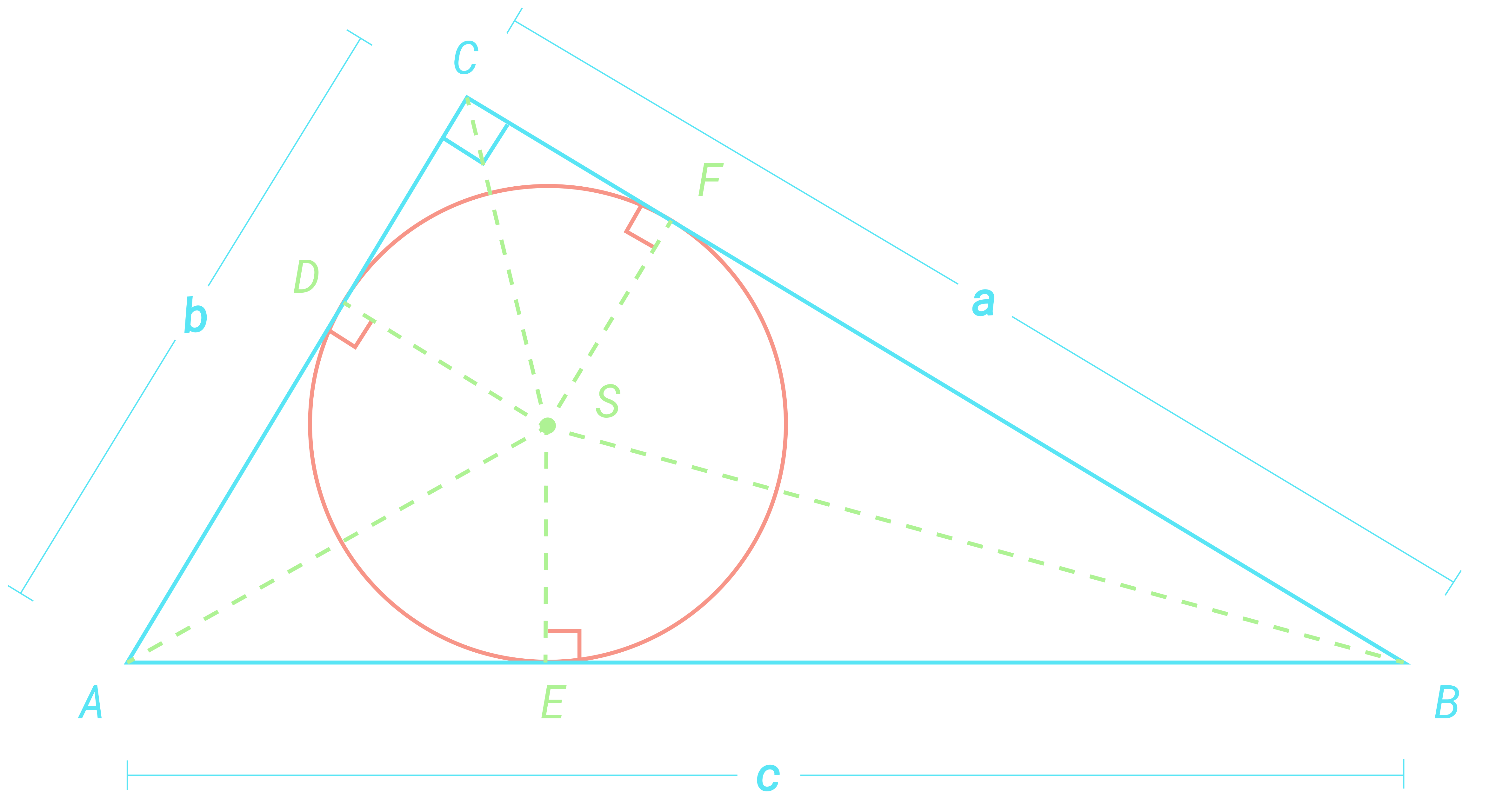
a) Bruk figuren til å forklare at a=BF+r og b=AD+r
Av figuren ser vi dessuten at c=AE+BEb) Vis at a+b−c=2r
c) Forklare at vi kan skrive arealet T av trekanten på to måter:
T=21⋅a⋅b og T=21⋅r⋅(a+b+c)
d) Bruk resultatene du fant i oppgavene b) og c) til å utlede Pytagoras' setning.
Oppgave 1 (6 poeng)
I en kortstokk er det 52 kort. Kortene er fordelt på de fire fargene hjerter, ruter, spar og kløver. Hver farge har 13 kort fordelt på verdiene 2 til 10, knekt, dame, konge og ess. Tenk deg at du skal trekke tilfeldig fem kort fra kortstokken.a) Bestem sannsynligheten for at du kommer til å trekke nøyaktig tre kort med verdi 10.
b) Bestem sannsynligheten for at du kommer til å trekke nøyaktig tre kort med samme verdi.
c) Bestem sannsynligheten for at alle kortene du kommer til å trekke, har samme farge.

Oppgave 2 (6 poeng)
Posisjonsvektoren til en partikkel er gitt vedr(t)=[t2−1,t3−t]
a) Tegn grafen til r når t∈[−23,23]. b) Bestem fertsvektoren v(t) og akselerasjonsvektoren a(t). c) Bruk CAS til å bestemme den minste banefarten til partikkelen.Oppgave 3 (4 poeng)
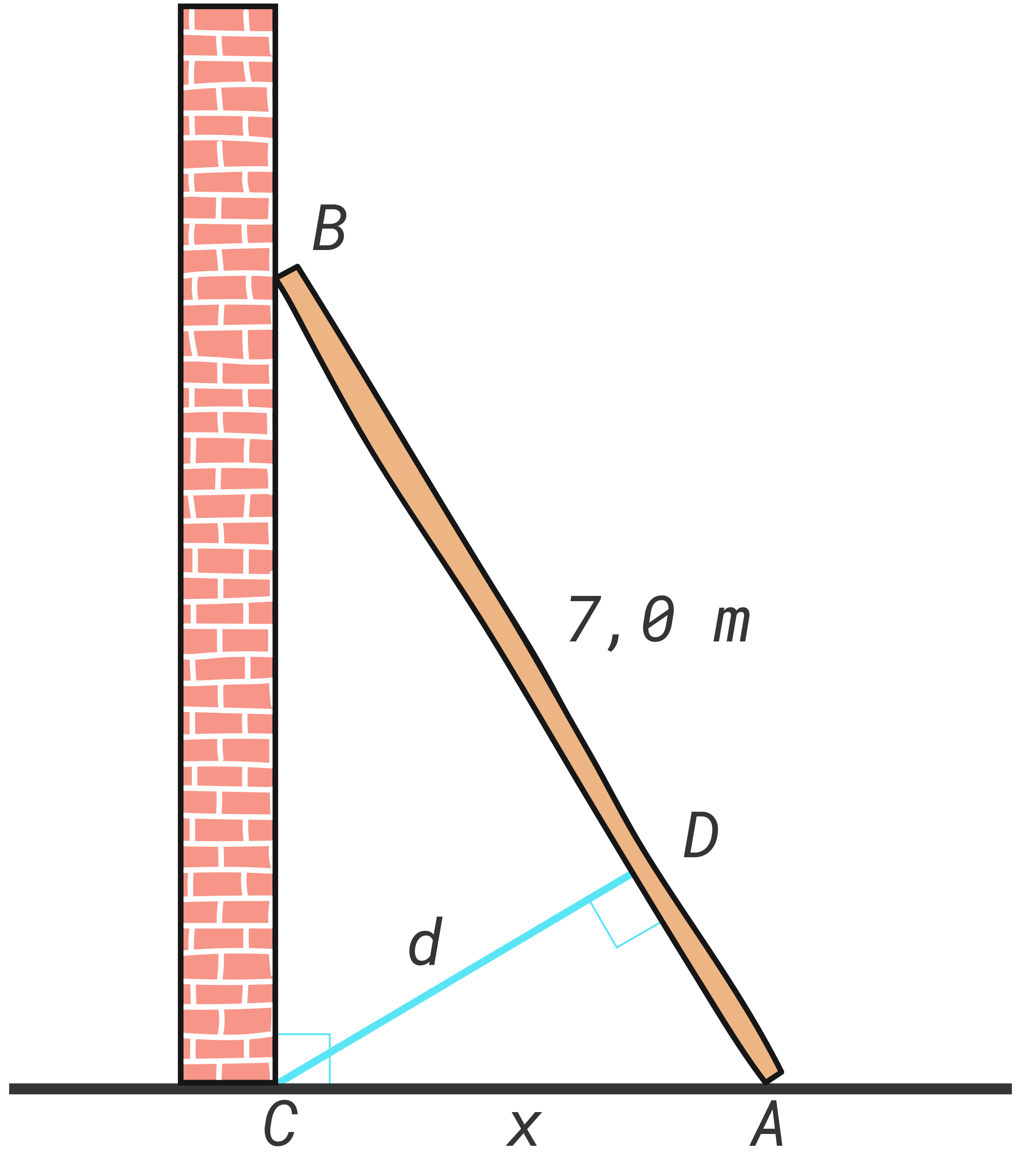
a) Vis at d=7x49−x2
b) Bestem x slik at d blir lengst mulig.
Hvor lang er d for denne verdien av x ?
Oppgave 4 (8 poeng)
Funksjonen f er gitt vedf(x)=2x3−6x2+5x
a) Bruk graftegner til å tegne grafen til f.
Grafen tilf har tre tangenter som går gjennom punktetA(4,3) .b) Forklar at x-koordinaten til tangeringspunktene må være løsning av likningen
x−4f(x)−3=f′(x)
c) Bruk CAS til å løse denne likningen. Bestem likningen til hver av tangentene.
La P(a,b) være et punkt i planet.d) Hva er det maksimale antallet tangenter grafen til fkan ha som går gjennom P?
Prøvesmak våre videoer
Mattevideo tilbyr fullstendig dekning av kursene 1P, 1PY, 1T, 2P, S1, R1, S2 og R2 innenfor videregående skole. Under har vi lagt ut noen smakebiter fra disse kursene, så du kan sjekke ut noe av det vi har å by på, før du bestemmer deg for å bli abonnent.1P - Polynomfunksjoner1PY - Prosentregning1T - Funksjonsbegrepet2P - Første gradS1 - LikningssettR1 - Å finn den deriverte ved å bruke derivasjonsreglerS2 - Aritmetiske og geometriske rekkerR2 - Sinusfunksjoner og cosinusfunksjoner

Lær å jobbe smarterepå 5 minutter
Det finnes mange ulike studieteknikker, utfordringen er ofte å finne de som fungerer best for deg. I oversikten under finner du enkelt de beste teknikkene.
Alle våre studietips er laget av vår superelev - med 6 i snitt fra vgs. Ingen av artiklene tar mer enn 5 minutter å lese - slik at du kan starte læringen så fort som mulig.
Hva skjer i hjernen når du lærer?
 Du møter noe nytt for første gang
Du møter noe nytt for første gang Du kobler den nye tingen med kunnskap du har fra før
Du kobler den nye tingen med kunnskap du har fra før Du repeter og styrker sammenhengene
Du repeter og styrker sammenhengene Du bruker kunnskapen
Du bruker kunnskapen

Vanlige utfordringer - og hvordan løse dem


Teknikkene som gjør deg til en superelev
La oss ringe deg, så finner vi en god løsning.









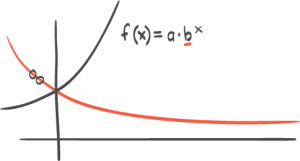



















a) Finn likningen for sirkelen.
b) Finn skjæringspunktene mellom sirkelen og koordinataksene.
c) Skisser sirkelen i et koordinatsystem

Avgjør om punktet A(7,2) ligger innenfor sirkelen.


Finn den gjennomsnittlige vekstfarten i periodene
a) [0,5] b) [5,10] c) [10,15]



- Sentrum i sirkelen ligg på linja y = x
- Sentrum i sirkelen ligg like langt frå origo som frå punktet A(6 , 0)
- Origo og punktet A ligg begge på sirkelperiferien
a) Teikn sirkelen i eit koordinatsystem.
b) Bestem ei likning for sirkelen.

a) Finn en formel for beløpet B på kontoen etter x år.
b) Hva er saldoen etter 20 år?
c) Tegn grafen til B(x).
d) Finn grafisk når saldoen er doblet.

Riktig svar!
300 kr betales uansett hvor mange kilometer man kjører, og så legger man til 5 kroner for hver kilometer kjørt.
Tabellen nedenfor viser hvor mange prosent av den norske befolkningen i aldersgruppen 16–74 år som røykte daglig i 2002, 2004, 2006, 2009 og 2012.

La x være antall år etter 2002. (La x = 0 svare til år 2002, x = 1 til år 2003, osv.)
- a) Bruk opplysningene i tabellen til å bestemme en lineær funksjon som viser utviklingen fra 2002 til 2012.
- b) Vurder om funksjonen kan brukes til å beskrive en videre utvikling fram mot år 2025.
f(x)=31,5x−1,3
f(x)=−1,3x−0,99
f(x)=−1,3x+31,5
Riktig svar!
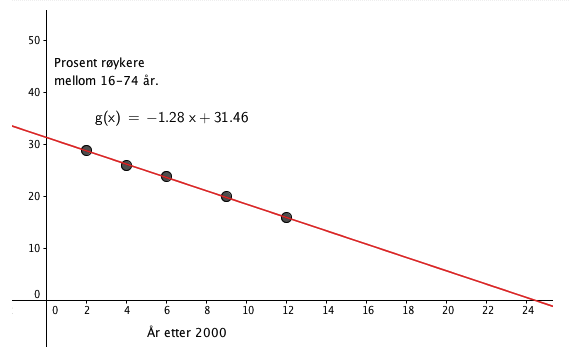
En brukbar modell er f(x)=−1,3x+31,5
f(x)=a⋅bx hvor b er et positivt tall
f(x)=x⋅ab hvor a er et positivt tall
Riktig svar!
Ja, fordi her er x en eksponent i funksjonen.
Løs likningen
24x⋅2x2=32
x=−5,x=1
x=−10,x=2
x=345
Riktig svar!
24x×2x2=32
24x+x2=25
Fra dette ser vi at 4x+x2=5, eller at: x2+4x−5=0. Når vi løser dette:
x=2−4±16+20=2−4±6
Som gir oss: x=−5 eller x=1
Løs likningen
22−x⋅21+2x=32
x=1
x=2
x=3−4
Riktig svar!
22−x⋅21+2x=32 22−x+1+2x=25 3+x=5 x=2
Hvilken av funksjonene er ikke en eksponentiell funksjon?
f(x)=10e−2x
g(x)=90⋅0,85x
h(x)=0,85xe
Riktig svar!
Her er x grunntallet i potensen.
Vi har en logistisk funksjon f(x)=1+2e−5x30 . Hvilken grenseverdi nærmer funkssjonen seg når x går mot uendelig?
0
10
30
Riktig svar!
Siden telleren blir 1.
Funksjonen f(x)=e2x kan skrives f(x)=ax, der ..
a=2
a=ln2
a=e2
Riktig svar!
Dette er en potensregel.
axy=(ax)y
Vi har en logistisk funksjon f(x)=1+2e−5x30 . Hva blir f(0) ?
0
10
30
Riktig svar!
f(x)=1+2e−5∗030
f(x)=1+230
f(x)=10
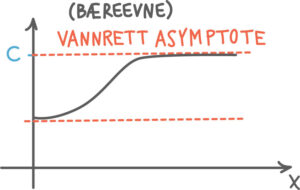
En populasjon blir beskrevet av en logistisk funksjon f(x)=1+b⋅e−cxa . Bæreevnen til populasjonen, er da det samme som
a
b
c
Riktig svar!
Fordi når x går mot uendelig vil nevneren gå mot 1.
Hva er IKKE riktig når det gjelder funksjonene f(x)=1+2e−5x1 og f(x)=1+2e−50x1 ?
f(0)=g(0)
Begge går mot samme verdi x går mot uendelig
f(2)=g(2)
Riktig svar!
Her vil det bli forskjell mellom eksponentene i f(x) og g(x) siden g(x) har -50x og f(x) har -5x.
Funksjonen f(x)=2x kan skrives f(x)=ekx, der ..
k=2
k=ln2
k=e2
Riktig svar!
eln nullerer hverandre ut.
Grafen til den deriverte til en logistisk funksjon har toppunkt i x = 10. Dette forteller at
Den logistiske funksjonen har toppunkt i x = 10
Den logistiske funksjonen stiger raskest i x = 10
f(10) = 0
Riktig svar!
Siden den deriverte viser hvor fort grafen stiger, og et toppunkt vil da vise hvor grafen stiger raskest.
Hvilken kommando gir logistisk regresjon i Geogebra?
Reglog
Du kan velge mellom reglog og reglogist
Du må bruke reglogist. (Reglog gir logaritmisk regresjon)
Riktig svar!
Dette må man bare huske.
I geogebra kan man gjøre regresjon med kommandoene regeksp og regeksp2. Gir begge eksponentiell regresjon?
Ja, ingen forskjell.
Ja, den ene gir funksjon av typen f(x)=a⋅bx, mens den andre gir funksjon av typen f(x)=a⋅ekx .
Nei.
Riktig svar!
Det er forskjell i måten funksjonsuttrykket blir.
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Tabellen nedenfor viser hvor mange prosent av den norske befolkningen i aldersgruppen 16–74 år som røykte daglig i 2002, 2004, 2006, 2009 og 2012.

La x være antall år etter 2002. (La x = 0 svare til år 2002, x = 1 til år 2003, osv.)
- a) Bruk opplysningene i tabellen til å bestemme en lineær funksjon som viser utviklingen fra 2002 til 2012.
- b) Vurder om funksjonen kan brukes til å beskrive en videre utvikling fram mot år 2025.

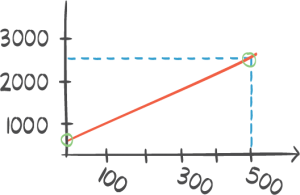
Tabellen ovenfor viser hvor langt Janne jogget noen uker etter at hun begynte å trene. Den
første uka jogget hun 3,4 km, den tredje uka jogget hun 5,1 km, og så videre.
a) Bestem den lineære funksjonen som passer best med tallene i tabellen ovenfor.
b) Hvor langt vil Janne jogge i uke 25 ifølge funksjonen i oppgave a) ?
c) I hvilken uke jogget Janne for første gang mer enn 10 km ifølge funksjonen i oppgave a) ?
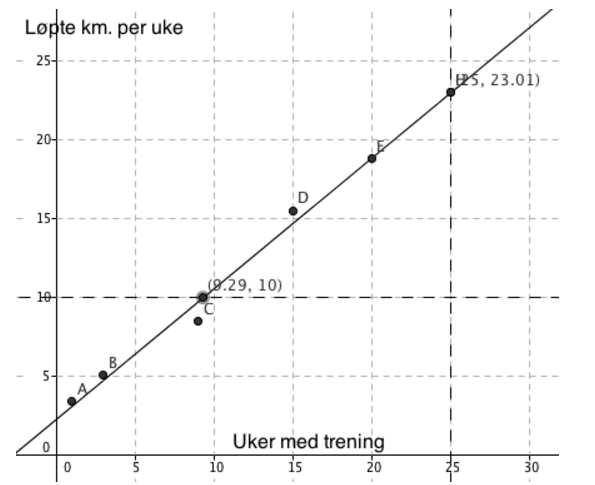
Bruker Geogebra og finner at den lineære funksjonen som passer best med de oppgitte data er :
y = 0,83x + 2,31
x er antall uker etter treningsstart.

Tabellen ovenfor viser hvor langt Janne jogget noen uker etter at hun begynte å trene. Den
første uka jogget hun 3,4 km, den tredje uka jogget hun 5,1 km, og så videre.
a) Bestem den lineære funksjonen som passer best med tallene i tabellen ovenfor.
b) Hvor langt vil Janne jogge i uke 25 ifølge funksjonen i oppgave a) ?
c) I hvilken uke jogget Janne for første gang mer enn 10 km ifølge funksjonen i oppgave a) ?

Avlesning av grafen i a viser at det skjer den niende treningsuken.

Tabellen ovenfor viser hvor langt Janne jogget noen uker etter at hun begynte å trene. Den
første uka jogget hun 3,4 km, den tredje uka jogget hun 5,1 km, og så videre.
a) Bestem den lineære funksjonen som passer best med tallene i tabellen ovenfor.
b) Hvor langt vil Janne jogge i uke 25 ifølge funksjonen i oppgave a) ?
c) I hvilken uke jogget Janne for første gang mer enn 10 km ifølge funksjonen i oppgave a) ?

Avlesning av grafen i a gir ca. 23 km.
Silje driver butikk. I slutten av mars opprettet hun en side på Facebook.
I slutten av april fant Silje ut at antall personer som hadde klikket «liker» på siden hennes x dager etter 31. mars,tilnærmet var gitt ved funksjonen f(x)=80⋅1,045x
Her svarer x=0 til 31. mars, x=1 til 1.april, x=2 til 2 . april, og så videre.
Anta at denne funksjonen også vil gjelde for mai.
a) Hvor mange personer hadde klikket «liker» på Siljes side før 1. april? Hvor mange prosent øker antall «liker» med per dag ?
b) Vil antall «liker» passere 1000 innen utgangen av mai ?
c) Bestem f(16)ogf(ˊ16)
Hva forteller disse verdiene om antall «liker» på Siljes side?
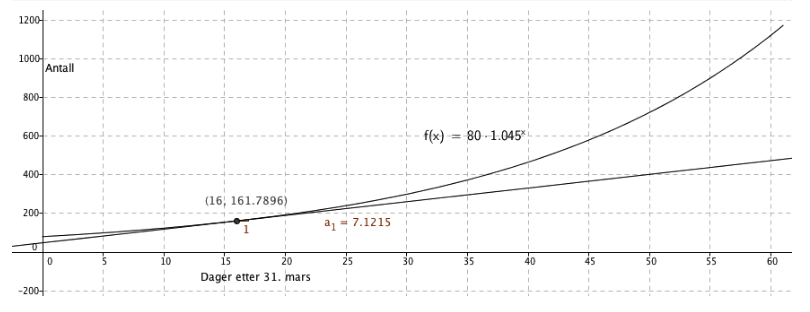
f(16) forteller hvor mange "likes" det var 16. april, 162.
f\'(16) forteller om den momentane endringen denne dagen, en økning på ca 7 "likes".
Silje driver butikk. I slutten av mars opprettet hun en side på Facebook.
I slutten av april fant Silje ut at antall personer som hadde klikket «liker» på siden hennes x dager etter 31. mars,tilnærmet var gitt ved funksjonen f(x)=80⋅1,045x
Her svarer x=0til 31. mars, x=1til 1.april, x=2 til 2 . april, og så videre.
Anta at denne funksjonen også vil gjelde for mai
a) Hvor mange personer hadde klikket «liker» på Siljes side før 1. april? Hvor mange prosent øker antall «liker» med per dag ?
b) Vil antall «liker» passere 1000 innen utgangen av mai ?
c) Bestem f(16)ogf(ˊ16)
Hva forteller disse verdiene om antall «liker» på Siljes side?
80 personer, ettersom f(0)=80⋅1,0450=80⋅1=80.
1,045 tilsvarerer en vekst på 4,5%.
Svaret blir da 80 personer og 4,5% vekst.
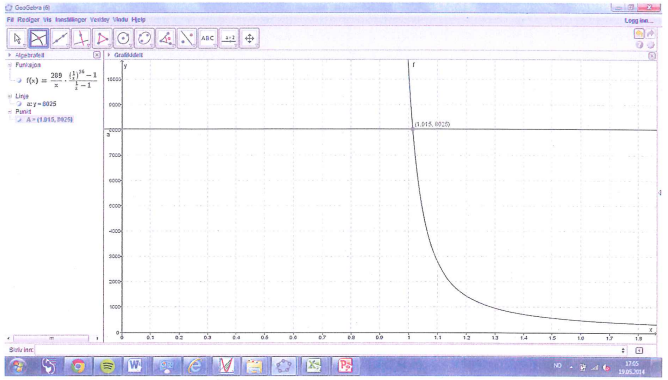
Frida ønsker å kjøpe en ny PC som koster 7 995 kroner.Butikken tilbyr henne å kjøpe PC-en på avbetaling. Hun må da betale 36 like store månedlige beløp. Det første skal hun betale om én måned. Den månedlige renten er 1,6 %. I tillegg må hun betale et engangsgebyr på 30 kroner.
- a) Forklar at dersom terminbeløpet er x kroner, så vil
1,016x+1,0162x+…+1,01636x=8025
Løs denne likningen
Frida vurderer å låne pengene i banken i stedet. Der må hun betale 289 kroner hver måned i 36 måneder. Hun må betale første beløp én måned etter at hun har tatt opp lånet. - b) Hvilken månedlig rente (i prosent) får hun i banken?Venninnen Elise har spart 650 kroner hver måned til en slik PC. Sparekontoen har en fast månedlig rente. I dag, like etter den 12. innbetalingen, har hun 8 107 kroner på kontoen.
- c) Bestem den månedlige renten (i prosent) Elise fikk i banken.
Summen av alle innbetalinger ført fra til like etter den 12. innbetalingen danner en geometrisk
rekke med a=650, som er det siste sparebeløpet hun nettopp har satt inn, n = 12 som er antall
ledd i rekken (antall sparebeløp) og k=1+100p hvor p er den ukjente sparerenten.
Vi vet at summen av rekken er lik kontobeløpet som er kroner 8107.
Jeg kan da løse følgende likning i GeoGebra
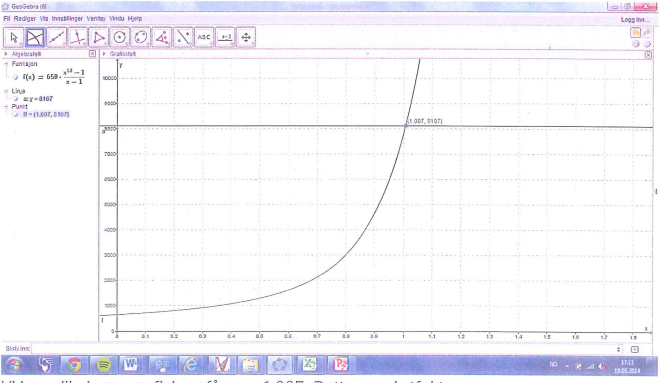
Elises månedlige sparerenten har vært på 0,7 %
Frida ønsker å kjøpe en ny PC som koster 7 995 kroner.Butikken tilbyr henne å kjøpe PC-en på avbetaling. Hun må da betale 36 like store månedlige beløp. Det første skal hun betale om én måned. Den månedlige renten er 1,6 %. I tillegg må hun betale et engangsgebyr på 30 kroner.
- a) Forklar at dersom terminbeløpet er x kroner, så vil
1,016x+1,0162x+…+1,01636x=8025
Løs denne likningen
Frida vurderer å låne pengene i banken i stedet. Der må hun betale 289 kroner hver måned i 36 måneder. Hun må betale første beløp én måned etter at hun har tatt opp lånet. -
b) Hvilken månedlig rente (i prosent) får hun i banken?
Venninnen Elise har spart 650 kroner hver måned til en slik PC. Sparekontoen har en fast månedlig rente. I dag, like etter den 12. innbetalingen, har hun 8 107 kroner på kontoen. - c) Bestem den månedlige renten (i prosent) Elise fikk i banken.
Situasjonen blir tilsvarende situasjonen i a). Men nå er månedsbeløpene Frida betaler kroner 289 og vekstfaktorene setter jeg nå som den ukjente x.Likningen blir nå som vist ved CAS i GeoGebra

Vekstfaktoren er på 1,015. Det betyr at
Den månedlige bankrenten er på 1,5 %.
Frida ønsker å kjøpe en ny PC som koster 7 995 kroner.Butikken tilbyr henne å kjøpe PC-en på avbetaling. Hun må da betale 36 like store månedlige beløp. Det første skal hun betale om én måned. Den månedlige renten er 1,6 %. I tillegg må hun betale et engangsgebyr på 30 kroner.
- a) Forklar at dersom terminbeløpet er x kroner, så vil
1,016x+1,0162x+…+1,01636x=8025
Løs denne likningen
Frida vurderer å låne pengene i banken i stedet. Der må hun betale 289 kroner hver måned i 36 måneder. Hun må betale første beløp én måned etter at hun har tatt opp lånet. -
b) Hvilken månedlig rente (i prosent) får hun i banken?
Venninnen Elise har spart 650 kroner hver måned til en slik PC. Sparekontoen har en fast månedlig rente. I dag, like etter den 12. innbetalingen, har hun 8 107 kroner på kontoen. - c) Bestem den månedlige renten (i prosent) Elise fikk i banken.
Jeg finner nå-verdiene av alle Fridas betalinger slik GeoGebrafiguren nedenfor illustrerer.

Summen av nå-verdiene må være lik kostprisen for PC-en pluss gebyret.
Da er 1,016x+1,0162x+…+1,01636x=7995+30=8025
Venstre side av likningen danner en geometrisk rekke med a1=1,016x,k=1,0161 og n = 36.
Summen av rekken er 1,016x⋅(1,0161)−1(1,0161)36−1
Likningen blir da 1,016x⋅(1,0161)−1(1,0161)36−1=8025
Jeg løser likningen ved CAS i GeoGebra

De månedlige beløpene er på 295 kroner.
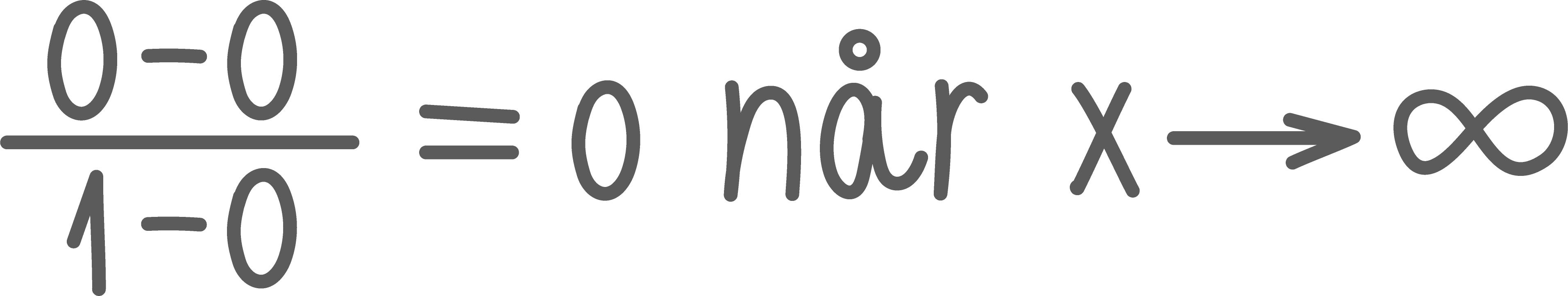




















Flott opplegg og undervisning😊
Tusen takk!
Gjorde unna R2 som privatist på et halvt år!! Mattevideo har gjort det mye lettere å fordøye et så tungt pensum på så kort tid. Tusen takk for hjelpa!!😊
Bra undervisning!
Jeg er fornøyd med videone deres det har hjulpet meg til å bestå matten i både Vgs og Uni . Så takk😊
Meget bra!
Tusen takk. Veldig flink lærer. Gode forklaringer.
Helt topp :D
Bra side.
Kjempebra!😊
Bra side. Veldig gode forklaringer😊
Tror dette kommer til å redde meg på noen prøver fremover. Takk! :D
takk for hjelpen
Takk for læreren av denne siden. Det er utrolig en bra side, fikk meg mye. Tusen hjertelig takk
Kan trygt anbefale Arne Hovland! Beste læreren jeg har hatt i løpet av drøyt 20 år med utdanning.
takk for denne siden :D min 1T mattelærer snakker så monotont og gjør matte så kjedelig at interessen svinner vekk og jeg sovner etter 5 minutter.