
VGS matematikk
1 - 2 - 3 klasse
1 - 2 - 3 klasse

Lær VGS matten fra A til Å
med de beste metodene


Enkelt å
holde fokus



Forstå det
vanskelige


Få god
oversikt


Øv på
riktig tema


Få hjelp når
du stopper opp

Tall og algebra
13:38
04:08

14:14
17:07
04:36
07:00

06:08
10:46
09:31
05:48

10:38
19:29
08:10
04:38

05:02
04:53

12:22
05:53

Økonomi
10:05
06:21
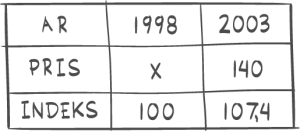
05:46
10:03

07:17
07:32

09:36

05:52

04:22
08:49

05:29
03:02
12:38
30:35
Sannsynlighet
13:40
02:07

15:13
11:15
04:57
11:36
09:06
12:21

12:21
16:05
Funksjoner
04:40
02:24

16:06
30:30
28:35
13:29
13:10
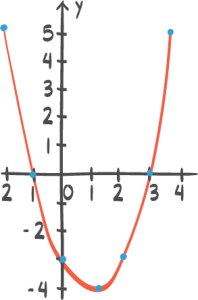
13:12
05:59
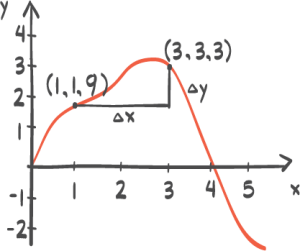
05:15
07:46
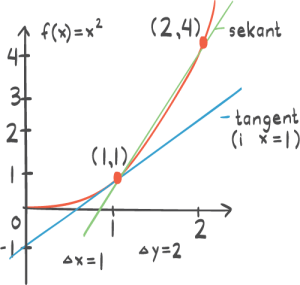
Oppgave 1 (3 poeng)
Nedenfor ser du hvor stor oppslutning Kristelig Folkeparti hadde ved stortingsvalgene i 2013 og 2017.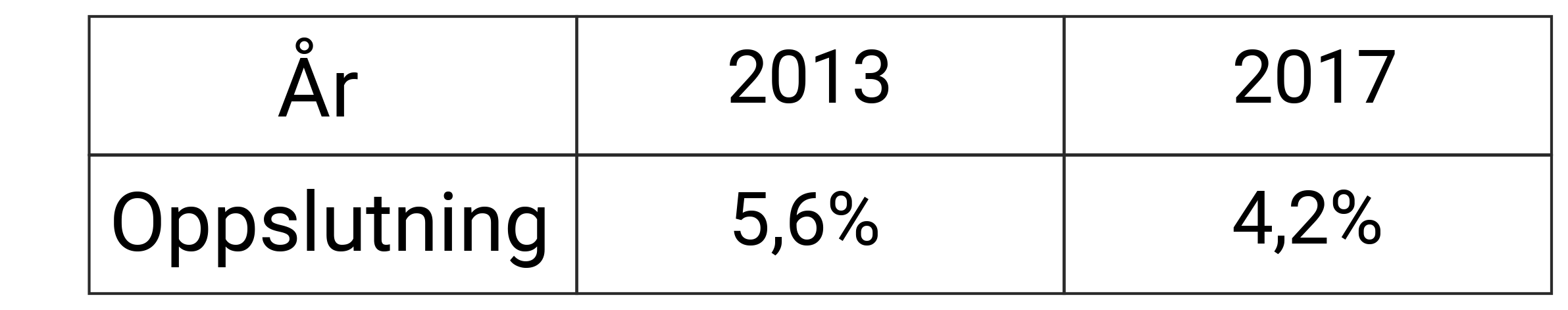
Oppgave 2 (2 poeng)
I en oppskrift står det at du trenger 4 dL melk og 500 g hvetemel for å lage 12 boller. Tenk deg at du har 1 L melk og 1,5 kg hvetemel. Hvor mange boller kan du lage dersom du følger oppskriften?Oppgave 3 (2 poeng)
I 2013 var indeksen for en vare 80. Varen kostet da 1000 kroner. I 2017 var indeksen for den samme varen 120. Hvor mye kostet varen i 2017 dersom prisen har fulgt indeksen?Oppgave 4 (2 poeng)
På et kart er avstanden mellom to byer 9 cm. I virkeligheten er avstanden 45 km. Bestem målestokken til kartet.Oppgave 5 (4 poeng)
Mads skal ta førerkortet for bil. Ved trafikkskolen koster det 13 000 kroner for den obligatoriske delen av føreropplæringen inkludert gebyrer. I tillegg koster det 600 kroner for hver kjøretime. a) Bestem en funksjon K som viser prisen K(x) kroner for å ta førerkortet dersom Mads bruker x kjøretimer. b) Tegn grafen til K i et koordinatsystem. c) Avgjør om prisen for å ta førerkortet og antall kjøretimer er proporsjonale størrelser.Oppgave 6 (2 poeng)
En fire år gammel moped koster i dag 8000 kroner. Mopedens verdi har avtatt med 12 % per år siden den var ny. Forklar hvilket av uttrykkene nedenfor som kan brukes til å finne hvor mye mopeden kostet da den var ny.Oppgave 7 (3 poeng)

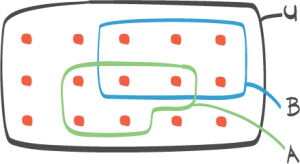
- Terningene viser samme antall øyne.
- Summen av antall øyne er 5 eller mindre.
Oppgave 8 (2 poeng)
Åpningen i toppen av en brusflaske har form som en sirkel med diameter 22 mm. Avgjør om et kronestykke med omkrets 66 mm kan puttes ned i flasken.Oppgave 9 (4 poeng)
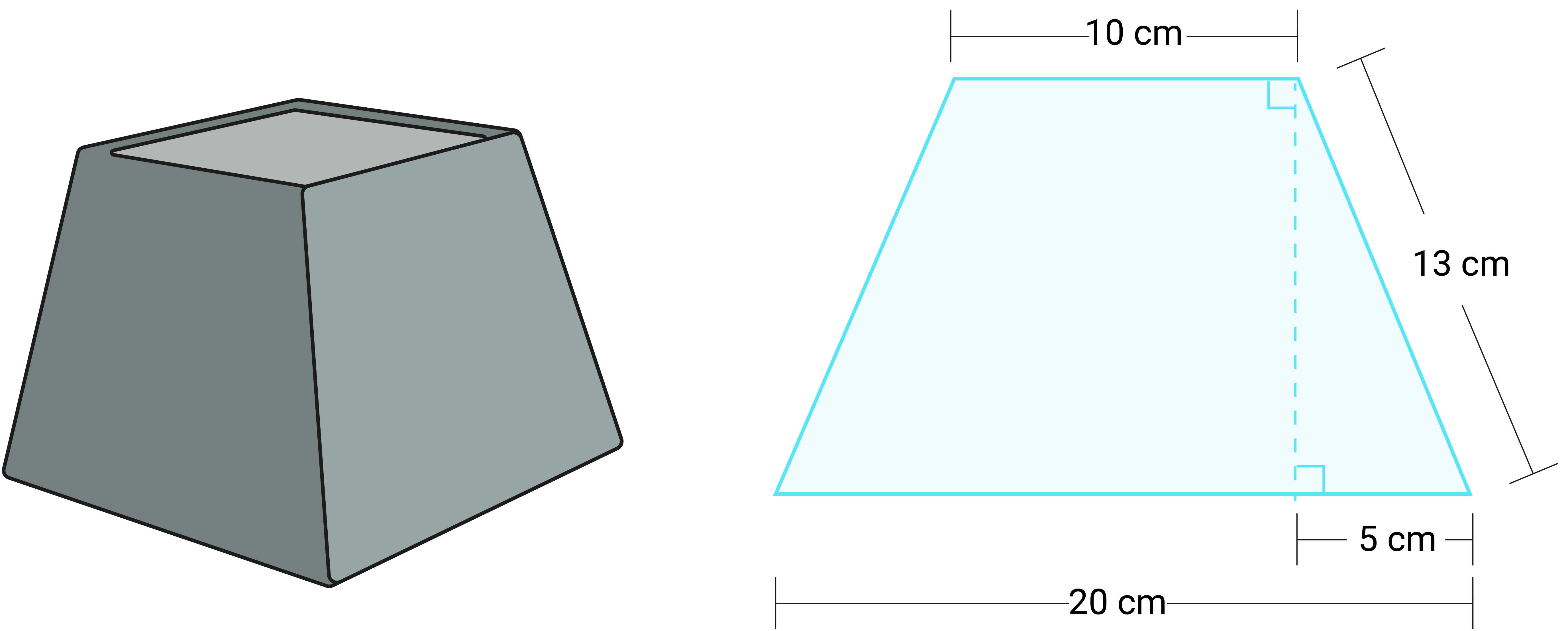
Oppgave 1 (6 poeng)
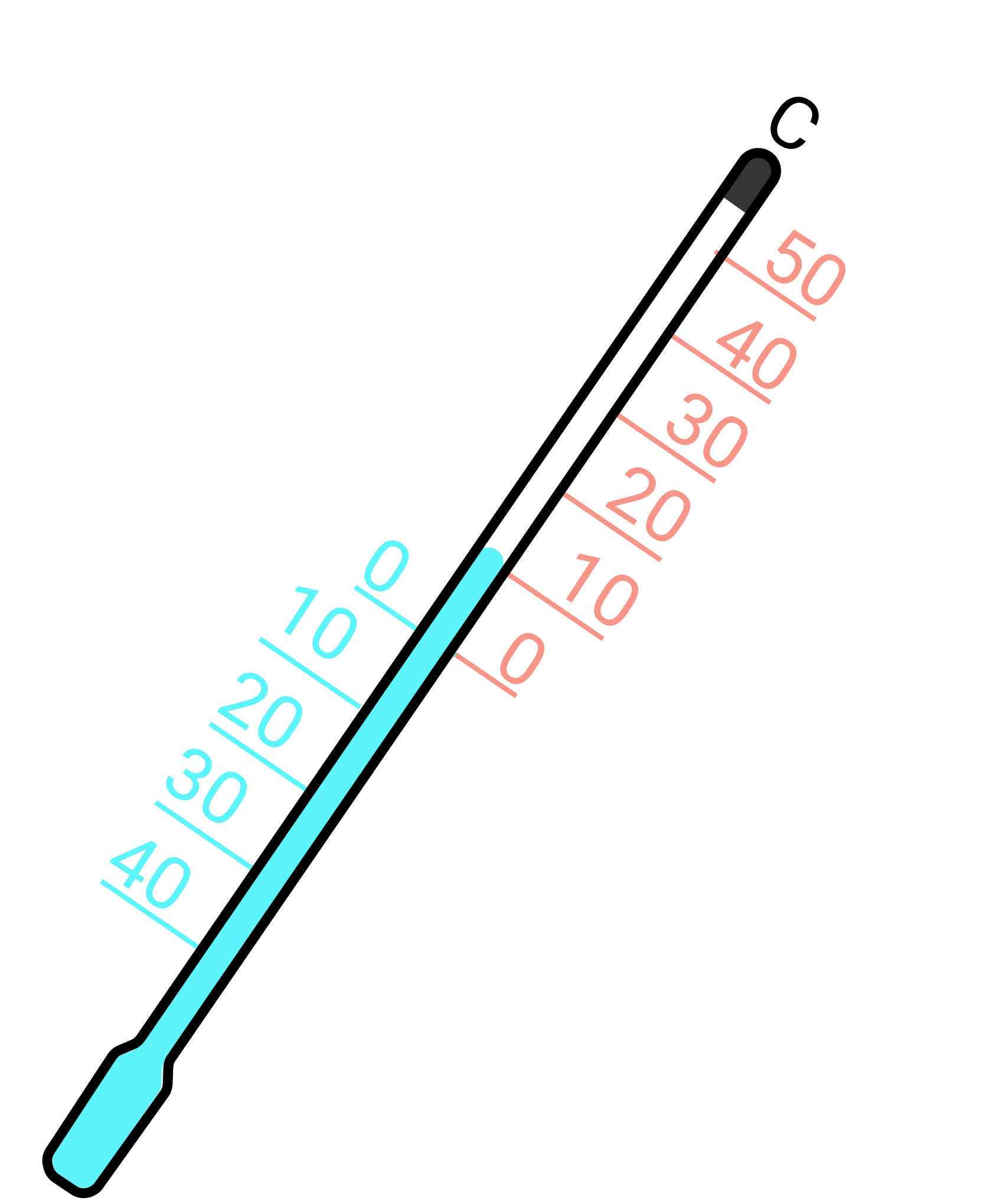
Oppgave 2 (4 poeng)
Silje har en timelønn på 210 kroner. Hun betaler 2 % av bruttolønnen i pensjonsavgift og har et skattetrekk på 32 %. En måned arbeidet hun 162,5 timer. a) Hvor mye fikk Silje utbetalt denne måneden? I 2017 fikk Silje utbetalt 47 736 kroner i feriepenger. Dette tilsvarer 12,0 % av feriepengegrunnlaget for 2017. b) Bestem feriepengegrunnlaget til Silje for 2017.Oppgave 3 (4 poeng)
Ved en videregående skole er det 640 elever. I en undersøkelse ble elevene spurt om når de legger seg kvelden før en skoledag.- av elevene svarte at de legger seg før klokka 23.
- av elevene som legger seg før klokka 23, har et karaktersnitt over fire.
- av elevene som legger seg etter klokka 23, har et karaktersnitt over fire.
Oppgave 4 (6 poeng)
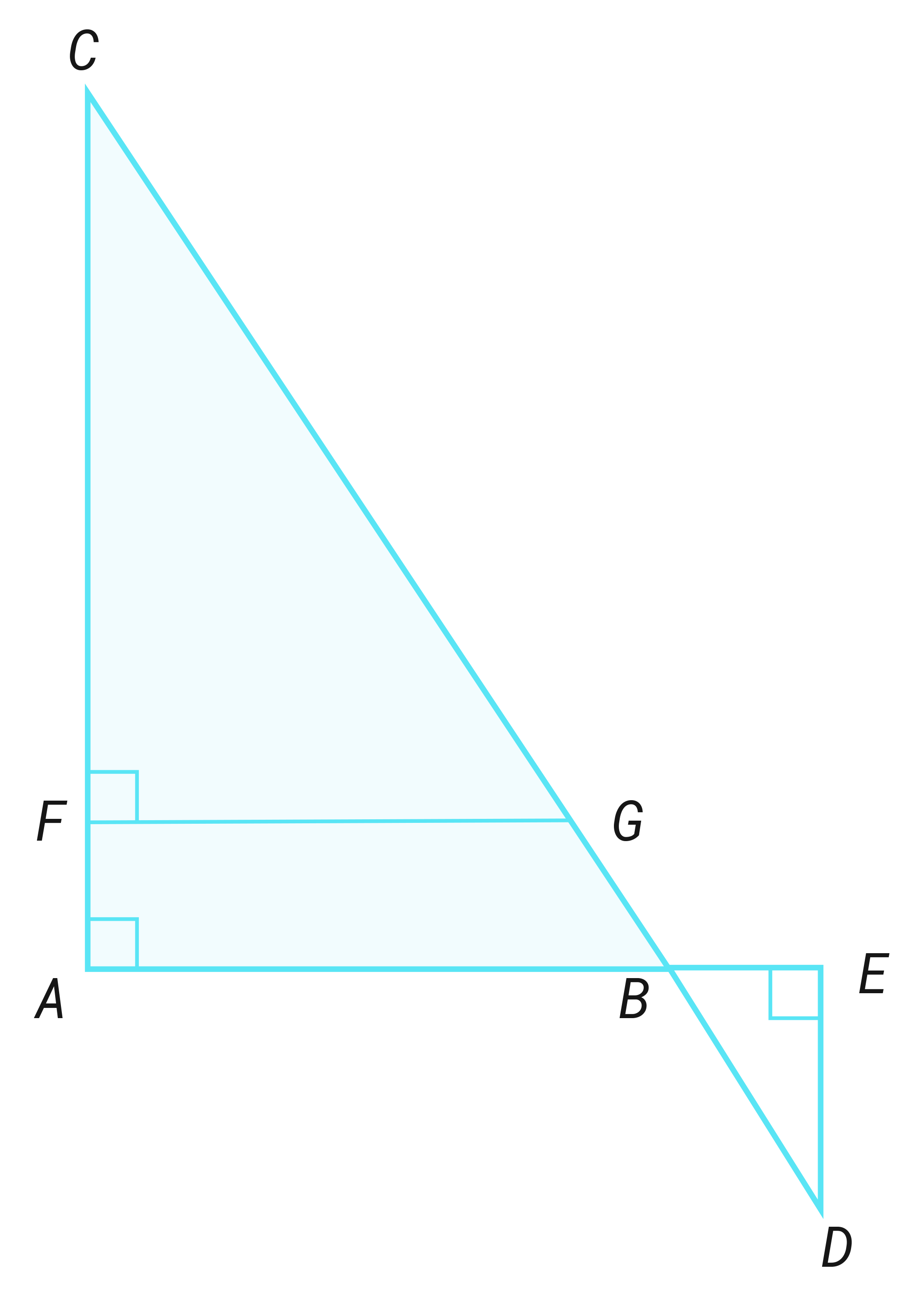
Oppgave 5 (5 poeng)
Et firma bruker i perioder skoleungdommer for å få unna diverse malerjobber. Ungdommene får timelønn etter alder. I tillegg til timelønn må firmaet betale feriepenger og arbeidsgiveravgift. Firmaet har beregnet at disse utgiftene utgjør 25 % av timelønnen. Du skal lage et regneark som vist nedenfor. I de hvite cellene skal firmaet registrere opplysninger. I de blå cellene skal du sette inn formler.- Timelønn og hvor stor prosentandel av lønnen som firmaet må beregne til feriepenger og arbeidsgiveravgift, skal registreres i celle B3, B4 og B5.
- Når alderen registreres, skal regnearket automatisk gi riktig timelønn.
- Totale kostnader for hver ungdom er summen av lønnen til ungdommen og utgiftene til feriepenger og arbeidsgiveravgift.

Oppgave 6 (6 poeng)

Oppgave 7 (5 poeng)
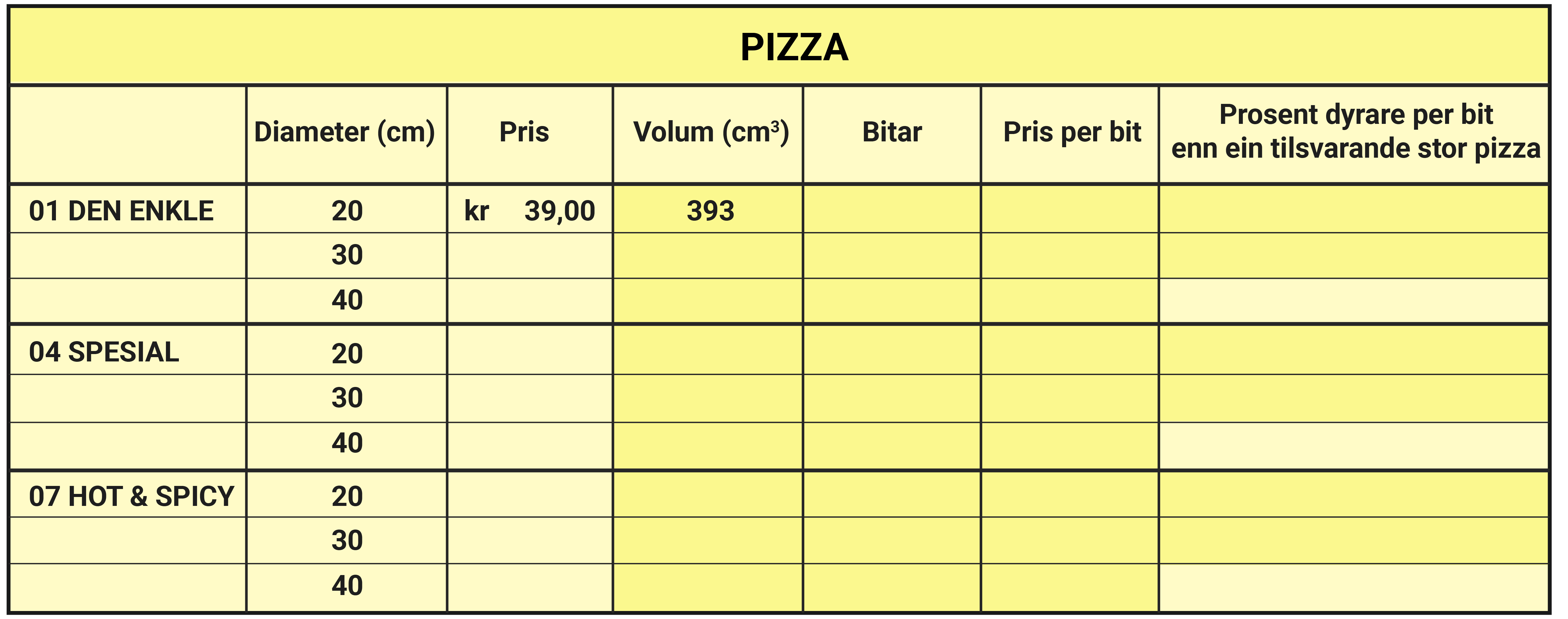
En pizzarestaurant tilbyr pizzaer i tre ulike størrelser.- Den minste pizzaen har en diameter på 20 cm, den mellomstore har en diameter på 30 cm, og den største har en diameter på 40 cm.
- Alle pizzaene er 1,25 cm tykke.
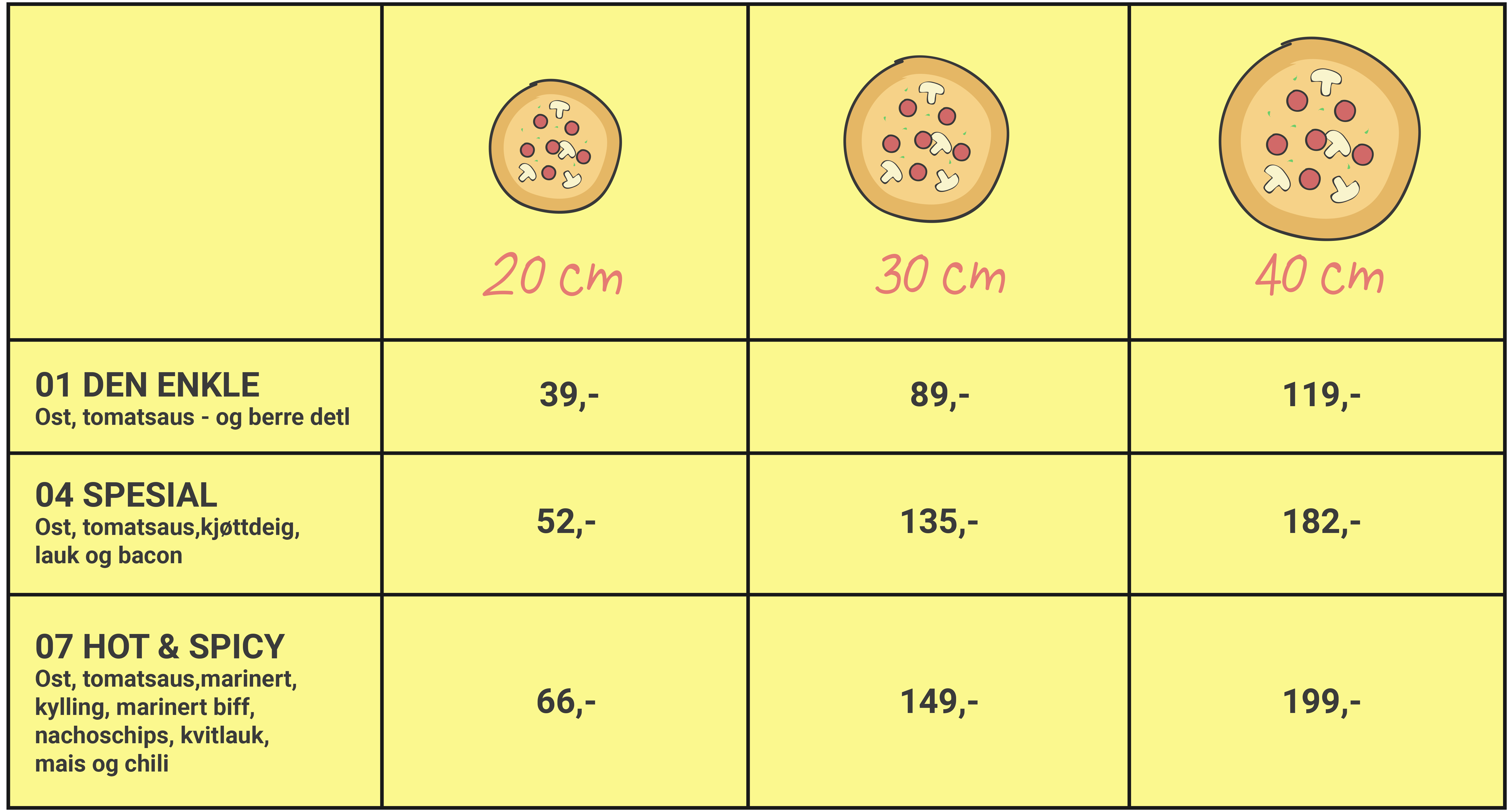
Gratis Prøvesmak
Superteknikker
En til en veiledning
Prøvesmak våre videoer
Mattevideo tilbyr fullstendig dekning av kursene 1P, 1PY, 1T, 2P, S1, R1, S2 og R2 innenfor videregående skole. Under har vi lagt ut noen smakebiter fra disse kursene, så du kan sjekke ut noe av det vi har å by på, før du bestemmer deg for å bli abonnent.1P - Polynomfunksjoner1PY - Prosentregning1T - Funksjonsbegrepet2P - Første gradS1 - LikningssettR1 - Å finn den deriverte ved å bruke derivasjonsreglerS2 - Aritmetiske og geometriske rekkerR2 - Sinusfunksjoner og cosinusfunksjoner

Lær å jobbe smarterepå 5 minutter
Det finnes mange ulike studieteknikker, utfordringen er ofte å finne de som fungerer best for deg. I oversikten under finner du enkelt de beste teknikkene.
Alle våre studietips er laget av vår superelev - med 6 i snitt fra vgs. Ingen av artiklene tar mer enn 5 minutter å lese - slik at du kan starte læringen så fort som mulig.
Hva skjer i hjernen når du lærer?
 Du møter noe nytt for første gang
Du møter noe nytt for første gang Du kobler den nye tingen med kunnskap du har fra før
Du kobler den nye tingen med kunnskap du har fra før Du repeter og styrker sammenhengene
Du repeter og styrker sammenhengene Du bruker kunnskapen
Du bruker kunnskapen

Vanlige utfordringer - og hvordan løse dem


Teknikkene som gjør deg til en superelev
En til en veiledning
Ønsker du en uforpliktende samtale om dine behov?
La oss ringe deg, så finner vi en god løsning.
La oss ringe deg, så finner vi en god løsning.

11:31
Teori 3

Annuitetslån. Vi regner ut de årlige rentene og avdragene til et lån på 60 000 når renta er 5 %, nedbetalingstiden er 3 år, det er 1 termin i året, og terminbeløpet er oppgitt til å være 22 033.
06:05
Teori 1

Lån. Du får se hva som menes med avdrag og renter. Det er viktig å vite hva som er kjennetegnene på serielån og annuitetslån, dette forklares her.
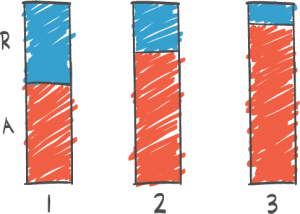

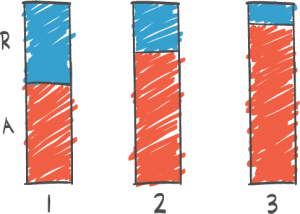

12:59
Teori 2

Serielån. Vi regner ut renter, avdrag og terminbeløp for hvert år når lånet er på 100 000 kr, renta er 4,1 %, og nedbetalingen er over 4 år, med 1 termin i året.




























Flott opplegg og undervisning😊
Tusen takk!
Gjorde unna R2 som privatist på et halvt år!! Mattevideo har gjort det mye lettere å fordøye et så tungt pensum på så kort tid. Tusen takk for hjelpa!!😊
Bra undervisning!
Jeg er fornøyd med videone deres det har hjulpet meg til å bestå matten i både Vgs og Uni . Så takk😊
Meget bra!
Tusen takk. Veldig flink lærer. Gode forklaringer.
Helt topp :D
Bra side.
Kjempebra!😊
Bra side. Veldig gode forklaringer😊
Tror dette kommer til å redde meg på noen prøver fremover. Takk! :D
takk for hjelpen
Takk for læreren av denne siden. Det er utrolig en bra side, fikk meg mye. Tusen hjertelig takk
Kan trygt anbefale Arne Hovland! Beste læreren jeg har hatt i løpet av drøyt 20 år med utdanning.
takk for denne siden :D min 1T mattelærer snakker så monotont og gjør matte så kjedelig at interessen svinner vekk og jeg sovner etter 5 minutter.