VGS matematikk
1 - 2 - 3 klasse
1 - 2 - 3 klasse
Lær VGS matten fra A til Å
med de beste metodene
Enkelt å
holde fokus
Forstå det
vanskelige
Få god
oversikt
Øv på
riktig tema
Få hjelp når
du stopper opp
Rekker
09:41
15:19
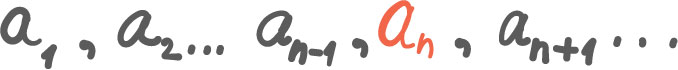
02:19
08:08
05:02
13:17
10:17
17:10
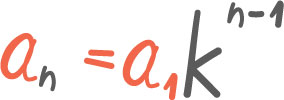
Algebra
45:37
21:34
34:11
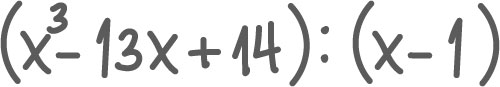
13:04
11:32
Derivasjon II
26:41
18:36
17:11
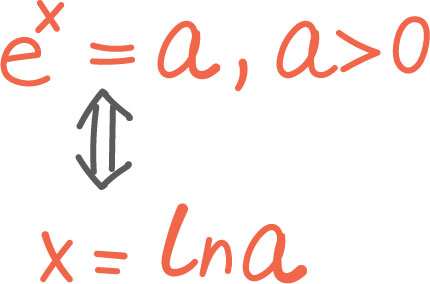
25:26
22:27
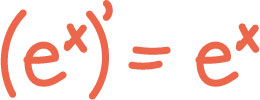
Økonomiske modeller
39:26
07:43
07:18
09:09
Sannsynlighet
11:02
06:23
37:35
10:14
05:57
04:31
10:29
10:50
02:05
06:44
Oppgåve 1 (4 poeng)
Deriver funksjonene
a)
b)
c)
Oppgåve 2 (5 poeng)
Funksjonen f er gitt veda) Bestem eventuelle topp- eller bunnpunkt på grafen til f .
b) Bestem eventuelle vendepunkt på grafen til f.
c) Lag en skisse av grafen til f.
Oppgåve 3 (3 poeng)
a) Forklar at polynomet
Oppgåve 4 (3 poeng)
Løs likningssystemet
Oppgåve 5 (3 poeng)
En rekke er gitt veda) Forklar at dette er en geometrisk rekke. Bestem et uttrykk for summen Sn av rekken.
b) Bestem summen av den uendelige rekken
Oppgåve 6 (4 poeng)
En tallfølgea) Skriv opp de fire første leddene i tallfølgen.
b) Vis at leddene
c) Vis at
Oppgåve 7 (4 poeng)
Laa) Bestem et uttrykk for inntekten
b) Bestem et uttrykk for overskuddet
Oppgåve 8 (4 poeng)
I et terningspill på et kasino blir det kastet to vanlige terninger. Dersom summen av antall øyne er 10, får spilleren 200 kroner. Blir summen av antall øyne 7, får spilleren 50 kroner. Dersom summen blir et annet tall, får ikke spilleren gevinst. La a være prisen en spiller må betale for ett spill, og X utbyttet til kasinoet ved én tilfeldig spilleomgang.
a) Skriv av og fyll ut tabellen nedenfor
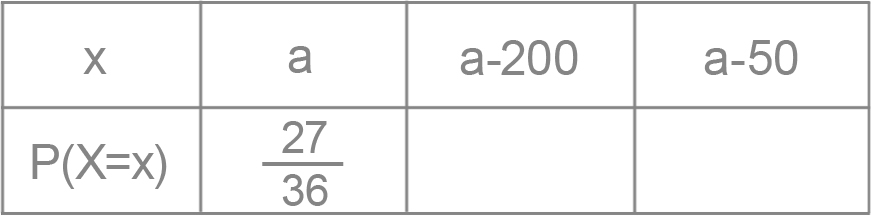
b) Hva bør kasinoet sette prisen a til for at de i det lange løp skal ha et gjennomsnittlig utbytte på 5 kroner per spill?
Oppgåve 9 (6 poeng)
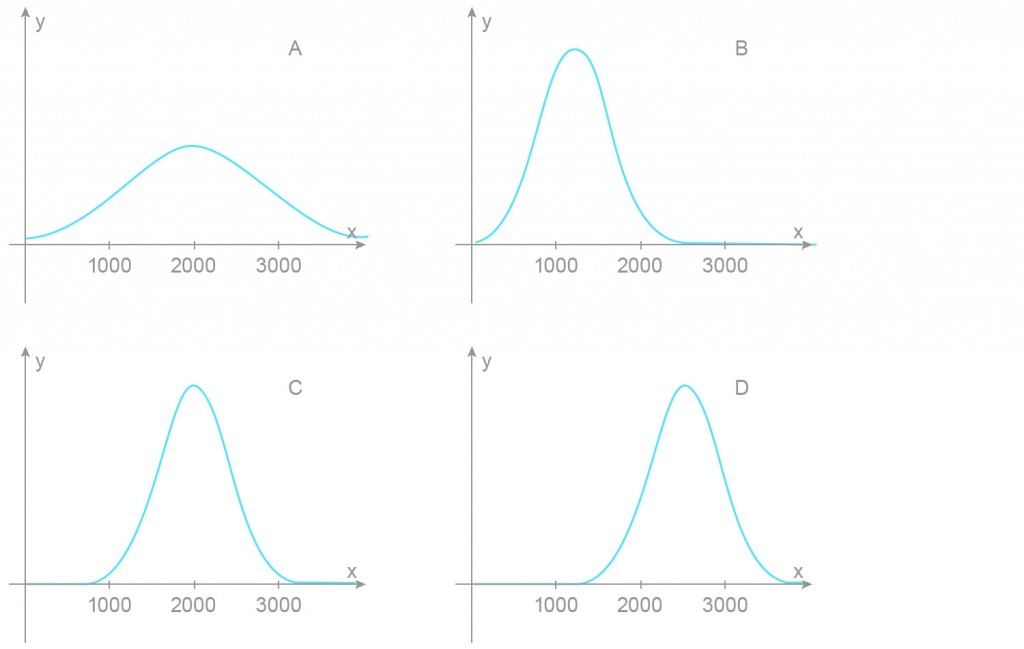
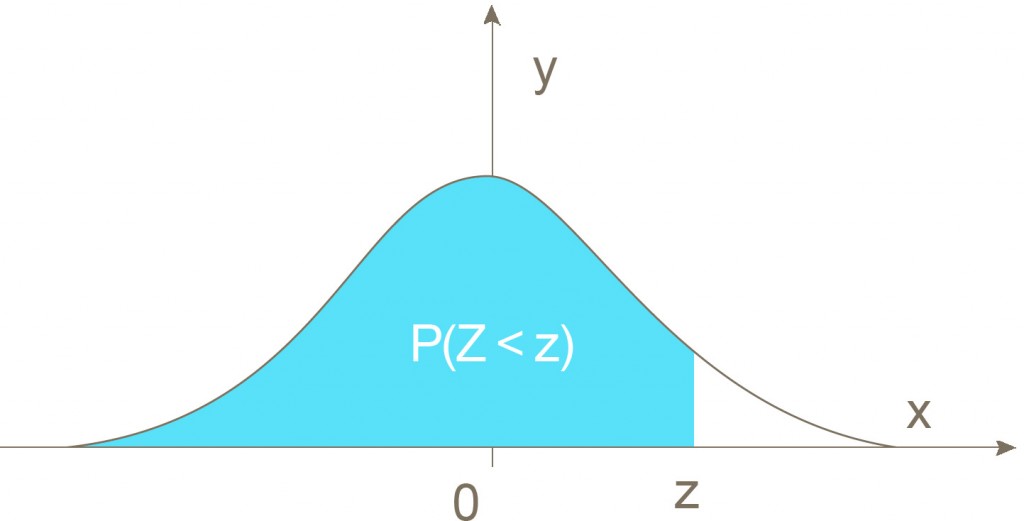
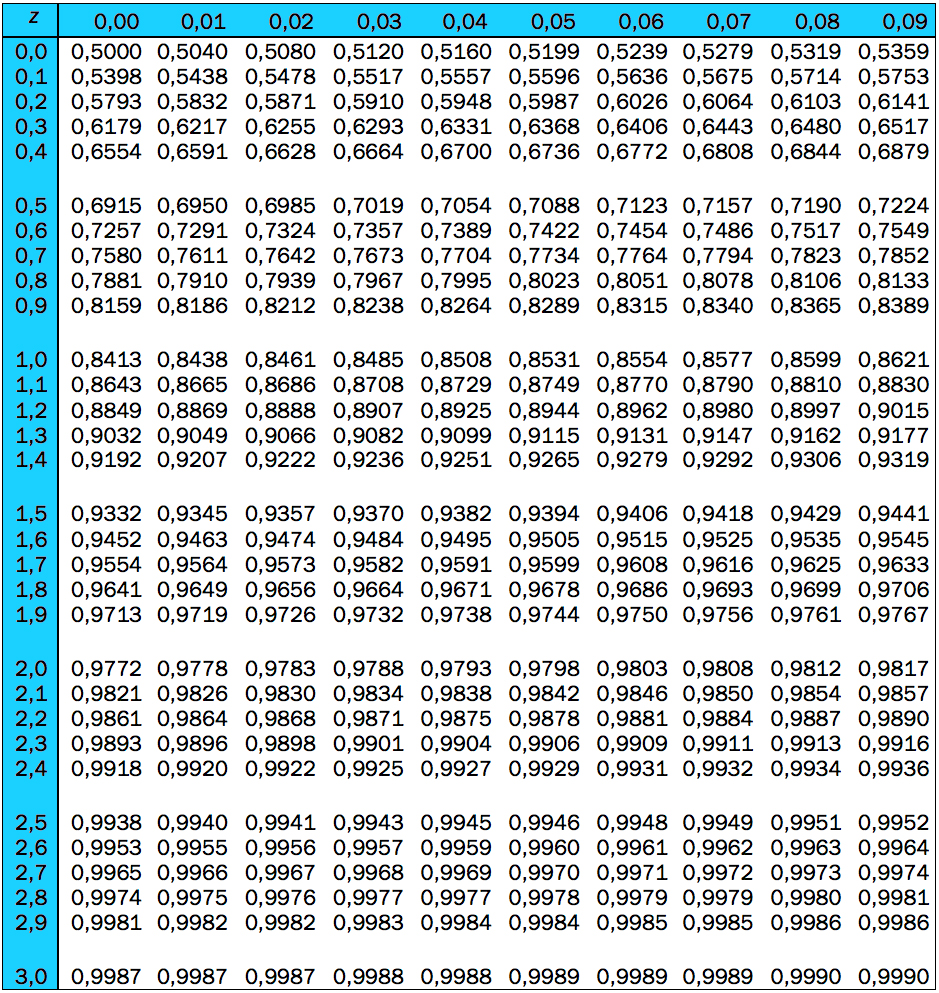
I denne oppgaven kan du få bruk for tabellen over standard normalfordeling i vedlegg 1. Levetiden X til en type lyspærer er normalfordelt med forventet levetid
a) Bestem sannsynligheten for at en tilfeldig valgt lyspære lyser færre enn 1600 timer.
b) Sannsynligheten er 90 % for at en tilfeldig valgt pære vil lyse i mer enn x timer. Bestem x.
c) Hvilken av de grafiske framstillingene nedenfor illustrerer X ? Begrunn svaret.
Oppgåve 1 (8 poeng)
Maria trener på et apparat i et treningssenter. La f(x) være treningseffekten, det vil si antall kilojoule som forbrennes per minutt, x minutter etter starten på treningsøkten. Funksjonen f er gitt ved
a) Bruk graftegner til å tegne grafen til
b) Bruk grafen til å bestemme treningseffekten etter 3 min og når treningseffekten er 50 kJ/min. Det samlede energiforbruket E, målt i kilojoule (kJ), i de første t minuttene av treningen er gitt ved
c) Bestem det samlede energiforbruket til Maria i løpet av de første 10 minuttene.
d) Anslå hvor lenge Maria må trene for at det samlede energiforbruket skal bli 1300 kJ.
Oppgåve 2 (8 poeng)
I 1992 skrev forskerne Ward og Whipp en artikkel i tidsskriftet Nature. De brukte regresjon til å hevde at de beste kvinnelige løperne før eller siden vil løpe like raskt som de mannlige på maratondistansen. I tabellene ser du gjennomsnittsfarten for verdensrekordløp i maraton for noen år. Menn:
Kvinner:
a) Lag lineære modeller f og g for farten til menn og kvinner. La x være antall år etter 1900.
b) Hvilket år vil kvinner løpe like raskt som menn, ifølge modellene? Raskeste mannlige løper (Dennis Kimetto) løp i 2014 med en gjennomsnittsfart på 5,72 m/s, mens beste kvinnelige løper (Tirfi Tsegaye) samme år løp med en gjennomsnittsfart på 5,01 m/s.
c) Hvordan vurderer du gyldigheten til modellene ovenfor ut fra disse resultatene? En logistisk modell for gjennomsnittlig maratonfart (i m/s) for mennenes rekordløp x år etter 1900 er gitt ved:
d) Vi tenker oss at vi kan bruke den logistiske modellen også etter år 2000. Hvilket år vil da maraton første gang bli løpt på under to timer? Maratondistansen er 42 195 m.
Oppgåve 3 (4 poeng)
Et fond på 50 millioner kroner ble opprettet 1. januar 2015. Hensikten er å dele ut et fast beløp til gode formål den 31.12. hvert år. Styret for fondet gikk først ut fra at den årlige avkastningen ville bli 10,0 %.a) Hvor mye penger kan maksimalt deles ut hvert år dersom fondet aldri skal gå tomt?
b) Når vil fondet være tomt for penger dersom det deles ut 8 millioner kroner hvert år?
Oppgåve 4 (4 poeng)
Energiinnholdet i de tre produktene smøreost, helmelk og hvitost kommer fra næringsstoffene fett, karbohydrater og proteiner. Tabellen nedenfor viser næringsinnhold og samlet energiinnhold i 100 g av hvert av de tre produktene.
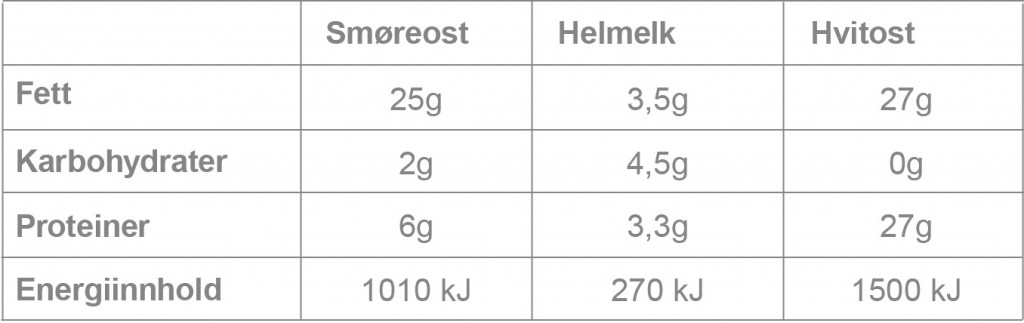
Sett opp et likningssystem og bruk CAS til å bestemme energiinnholdet (i kJ) i 1 g fett, 1 g karbohydrater og 1 g proteiner.
Vedlegg 1 Standard normalfordeling
Tabellen viser 
Gratis Prøvesmak
Superteknikker
En til en veiledning
Prøvesmak våre videoer
Mattevideo tilbyr fullstendig dekning av kursene 1P, 1PY, 1T, 2P, S1, R1, S2 og R2 innenfor videregående skole. Under har vi lagt ut noen smakebiter fra disse kursene, så du kan sjekke ut noe av det vi har å by på, før du bestemmer deg for å bli abonnent.1P - Polynomfunksjoner1PY - Prosentregning1T - Funksjonsbegrepet2P - Første gradS1 - LikningssettR1 - Å finn den deriverte ved å bruke derivasjonsreglerS2 - Aritmetiske og geometriske rekkerR2 - Sinusfunksjoner og cosinusfunksjoner
Lær å jobbe smarterepå 5 minutter
Det finnes mange ulike studieteknikker, utfordringen er ofte å finne de som fungerer best for deg. I oversikten under finner du enkelt de beste teknikkene.
Alle våre studietips er laget av vår superelev - med 6 i snitt fra vgs. Ingen av artiklene tar mer enn 5 minutter å lese - slik at du kan starte læringen så fort som mulig.
Hva skjer i hjernen når du lærer?
Du møter noe nytt for første gang
Du kobler den nye tingen med kunnskap du har fra før
Du repeter og styrker sammenhengene
Du bruker kunnskapen
Vanlige utfordringer - og hvordan løse dem
Teknikkene som gjør deg til en superelev
En til en veiledning
Ønsker du en uforpliktende samtale om dine behov?
La oss ringe deg, så finner vi en god løsning.
La oss ringe deg, så finner vi en god løsning.
05:36
Teori 1
Vi varmer opp til polynomdivisjon, ved å se på divisjon av vanlige tall.
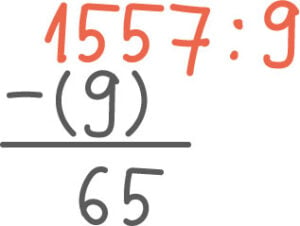
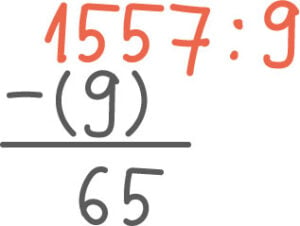
I det kapittelet vi nå er i, skal vi drive med polynomdivisjon. Og det handler om å dele polynomer på hverandre, altså sånne uttrykk med x eller x i annen eller sånne ting. Men for at vi skal skjønne den metoden, så er det lurt å gå tilbake til noe vi har lært en gang i tiden, nemlig å dele vanlige tall på hverandre, divisjonsalgoritmen som det heter.
Quiz section 0
Hva handler polynomdivisjon om?
Å dele polynomer på hverandre.
Å multiplisere polynomer.
Å addere polynomer.
Oppsummer det viktigste på 1-2-3,
klikk her for 10 sekunders quiz
klikk her for 10 sekunders quiz
Oppsummer det viktigste på 1-2-3
Så vi tar et eksempel. Vi skal ta to eksempler, men det første er tusen fem hundre og femtisyv delt på ni. La oss bare se hvordan vi gjorde den slags igjen.
Quiz section 1
Hvor mange eksempler skal vi gå gjennom først?
Fire
To
Tre
Da var vel greia at vi finner.
Quiz section 2
Hva er det første steget i divisjonsalgoritmen?
Legge sammen divisoren og dividenden.
Multiplisere divisoren med dividenden.
Finne hvor mange ganger divisoren går opp i de første sifrene.
Vi prøver jo kanskje med en del på ni, men det går liksom ikke.
Quiz section 3
Hva gjør vi hvis det første sifferet er mindre enn divisoren?
Skriver ned null.
Tar med neste siffer.
Stopper delingen.
Det er for lite, så da tar vi med ett siffer til. Femten delt på ni.
Quiz section 4
Hva gjør vi når tallet fortsatt er for lite til å dele på divisoren?
Tar med enda et siffer til.
Legger til null i svaret.
Multipliserer divisoren.
Og da er jo poenget at da skriver vi én fordi det går én gang, sier vi.
Quiz section 5
Hva skriver vi i kvotienten når divisoren går én gang opp i tallet?
9
0
1
Femten delt på ni.
Quiz section 6
Hvor mange ganger går 9 opp i 15?
2 ganger
3 ganger
1 gang
Og så gjør vi sånn. Én gang ni, og så skriver vi bare opp igjen i der.
Quiz section 7
Hva gjør vi etter å ha funnet hvor mange ganger divisoren går opp i tallet?
Multipliserer kvotienten med divisoren og skriver resultatet under.
Deler kvotienten på divisoren.
Legger kvotienten til divisoren.
Og så setter vi en strek sånn, og så minus, ser vi. Det trekker vi fra det.
Quiz section 8
Hva gjør vi med resultatet etter multiplikasjonen?
Trekker det fra tallet over.
Legger det til tallet over.
Skriver det som sluttresultat.
Og da er det sånn at vi tenker nå bare på femten. Femten minus ni, det er vel seks.
Quiz section 9
Hva finner vi når vi trekker produktet fra tallet over?
Resten
Kvotienten
Divisoren
Også henter vi ned et femtall til fordi seks delt på ni går ikke nå, men derimot hvis vi henter det femtitallet som står der oppe, så blir det sekstifem, og så gjør vi noe av det samme. Sekstifem delt på ni.
Quiz section 10
Hva gjør vi hvis resten er mindre enn divisoren?
Henter ned neste siffer fra dividenden.
Avslutter delingen.
Legger til null i kvotienten.
Nå er det ikke noe tall i ni-gangen som er sekstifem. Men vi vet kanskje at sekstitre er i ni-gangen. Det er det største tallet som er nesten sekstifem.
Quiz section 11
Hva gjør vi hvis divisoren ikke går opp i tallet nøyaktig?
Avrunder oppover til neste multiplum.
Legger til flere nuller til tallet.
Finner det største multiplum som er mindre enn tallet.
Det største tallet som er mindre enn sekstifem som er i ni-gangen, og det er sju. Sju ganger ni, så derfor skriver vi sju der. Da sier vi at det går sju ganger. Sju ganger ni, og så skriver vi da sekstitre. Så først sekstifem delt på ni, tar vi det største tallet, så får vi sju. Sju ganger ni, går vi tilbake igjen, og så skriver det vi da får, og så er det samme mølla, det vil si minus.
Quiz section 12
Hvorfor skriver vi tallet 7 i kvotienten når vi deler 65 på 9?
Fordi 9 ganger 7 er det største produktet under 65.
Fordi 9 ganger 7 er over 65.
Fordi 7 er resten.
Sånn.
Quiz section 13
Hva gjør vi etter å ha funnet neste siffer i kvotienten?
Avslutter delingen.
Gjentar prosessen med subtraksjon og nedhenting av sifre.
Multipliserer kvotienten med en ny divisor.
Så tar vi bare sekstifem minus sekstitre, og da får vi to. Og legg merke til at det blir alltid litt mindre enn det som står der oppe, fordi vi har truffet riktig. Hadde vi skrevet seks der i stedet, så hadde vi tatt seks ganger ni, og så hadde vi fått seks ganger ni. Det er vel femtifire da. Da hadde det blitt for mye her nede.
Quiz section 14
Hva får vi når vi trekker 63 fra 65?
0
4
2
Så vi må ha sju der. Sju ganger ni er sekstitre, og så hadde vi to nå, sånn. Og så gjør vi det samme vi gjorde i stad, og det vil si vi henter ned det tallet som står igjen der oppe, henter bare ned et tall. Tjuesju.
Quiz section 15
Hvorfor er det viktig å velge det største multiplum som er mindre enn tallet vi deler?
For å unngå å få null i resten.
For å få en større kvotient.
For å minimere resten og fortsette delingen korrekt.
Tjuesju delt på ni, det er tre.
Quiz section 16
Hva gjør vi etter å ha hentet ned det siste sifferet?
Avslutter regnestykket.
Multipliserer det nye tallet med divisoren.
Deler det nye tallet på divisoren.
Så det gikk opp til og med. Det er en fordel. Tre ganger ni er tjuesju.
Quiz section 17
Hva indikerer det når resten blir null?
At vi har gjort en feil.
At delingen går opp.
At vi må fortsette delingen.
Og så tar vi minus det også, og da blir det null, sånn. Og nå er det ikke noe mer som står igjen der oppe, og det betyr at når vi ikke har mer igjen her oppe, alt har vi liksom hentet ned og delt, samtidig så ble det ingenting til overs. Da gikk stykket opp, så vi kan si at tusen fem hundre og femtisyv delt på ni, det blir etthundreogsyttitre.
Quiz section 18
Hva betyr det når det ikke er flere sifre å hente ned?
At vi må legge til desimaler.
At vi starter på nytt.
At delingen er ferdig.
La oss si.
Quiz section 19
Hva skjer hvis delingen ikke går opp?
Vi får en feil kvotient.
Vi må dele på nytt.
Vi får en rest.
Delingen ikke går opp.
Quiz section 20
Når delingen ikke går opp, da får vi noe som heter rest.
Quiz section 21
Hva kalles tallet som blir igjen når delingen ikke går opp?
Kvotient
Rest
Divisor
Det som blir igjen.
Quiz section 22
Og hvis vi tar nesten det samme da, tusen fem hundre og femtini delt på ni.
Quiz section 23
Hva skjer hvis vi deler 1559 på 9?
Delingen går opp uten rest.
Vi får en rest.
Vi får null i kvotient.
Da vil jo ting være veldig likt i starten fordi vi kan begynne med femten delt på ni. Det gikk én gang. To ganger ni er atten, det blir for stort, ikke sant, så én gang ni er ni, og så tok vi minus det.
Quiz section 24
Femten minus ni. Da fikk vi seks, hentet ned. Så nå får vi repetert det vi gjorde der oppe egentlig. Sekstifem delt på ni. Det gikk en sju ganger var det vel.
Quiz section 25
Sju ganger ni, det blir sekstitre.
Quiz section 26
Minus.
Quiz section 27
Sånn. Sekstifem minus sekstitre, det er to, men nå står det ikke sju, nå står det ni. Så nå blir det tjueni.
Quiz section 28
Tjueni delt på.
Quiz section 29
Ni, det går fortsatt tre ganger. [..] Hadde vi tatt fire, så hadde vi fått trettiseks, så det blir for mye. Så det blir tre. Tre ganger ni, tjuesju. Men nå skal vi se hva som skjer nå.
Quiz section 30
Nå får vi en to, og nå er det ikke mer der oppe.
Quiz section 31
Vi kunne gjort sånn at vi bare lager et komma der, og så henter han ned null. Det hadde gått an, men alternativet er det jeg gjør nå, å bare si at det blir igjen noe.
Quiz section 32
Ja, pluss.
Quiz section 33
Hva kan vi gjøre hvis vi ønsker å fortsette delingen etter å ha fått en rest?
Multiplisere resten med divisoren.
Avslutte delingen.
Legge til et komma og null i dividenden.
To delt på.
Quiz section 34
Ni. Pluss to niendedeler.
Quiz section 35
Hvordan kan vi uttrykke resten som en brøk?
Dividenden delt på resten.
Resten delt på divisoren.
Divisoren delt på resten.
På ungdomsskolen kanskje du skrev etthundreogsyttitre og to ned, eller uten det plusstegn.
Quiz section 36
Hva betyr det å skrive svaret som et blandet tall?
Å ignorere resten.
Å skrive svaret kun som en brøk.
Å kombinere heltallsdelen med brøkdelen.
Quiz section 37
Quiz section 38
08:53
Teori 2
Polynomdivisjon (med og uten rest).
03:14
Teori 3
Polynomdivisjon og faktorisering.
03:51
Teori 4
Hva kan polynomet deles på? Et polynom kan deles på (x - a) dersom polynomet har a som nullpunkt. Vi ser på hvorfor det er slik.
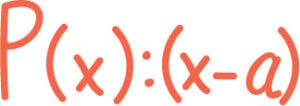
11:35
Oppgave 1
Gitt funksjonen
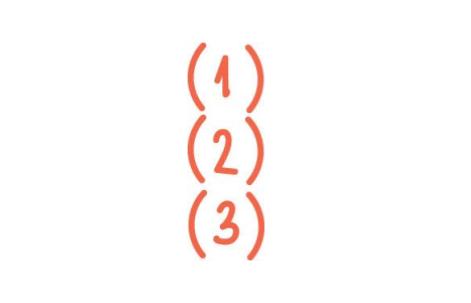
a) Undersøk om f(x) er delelig med: 1) (x-1), 2) (x+1), 3) (x-2)
b) Faktoriser f(x) .
a) Undersøk om f(x) er delelig med: 1) (x-1), 2) (x+1), 3) (x-2)
b) Faktoriser f(x) .
02:09
Oppgave 2
Bestem tallet a slik at divisjonen går opp.
07:47
Oppgave 3
Gitt likningen .
Undersøk om 0, 1, eller 2 er løsning på likningen.
Løs deretter likningen.
Undersøk om 0, 1, eller 2 er løsning på likningen.
Løs deretter likningen.
12:40
Oppgave 4
Forkort brøken .
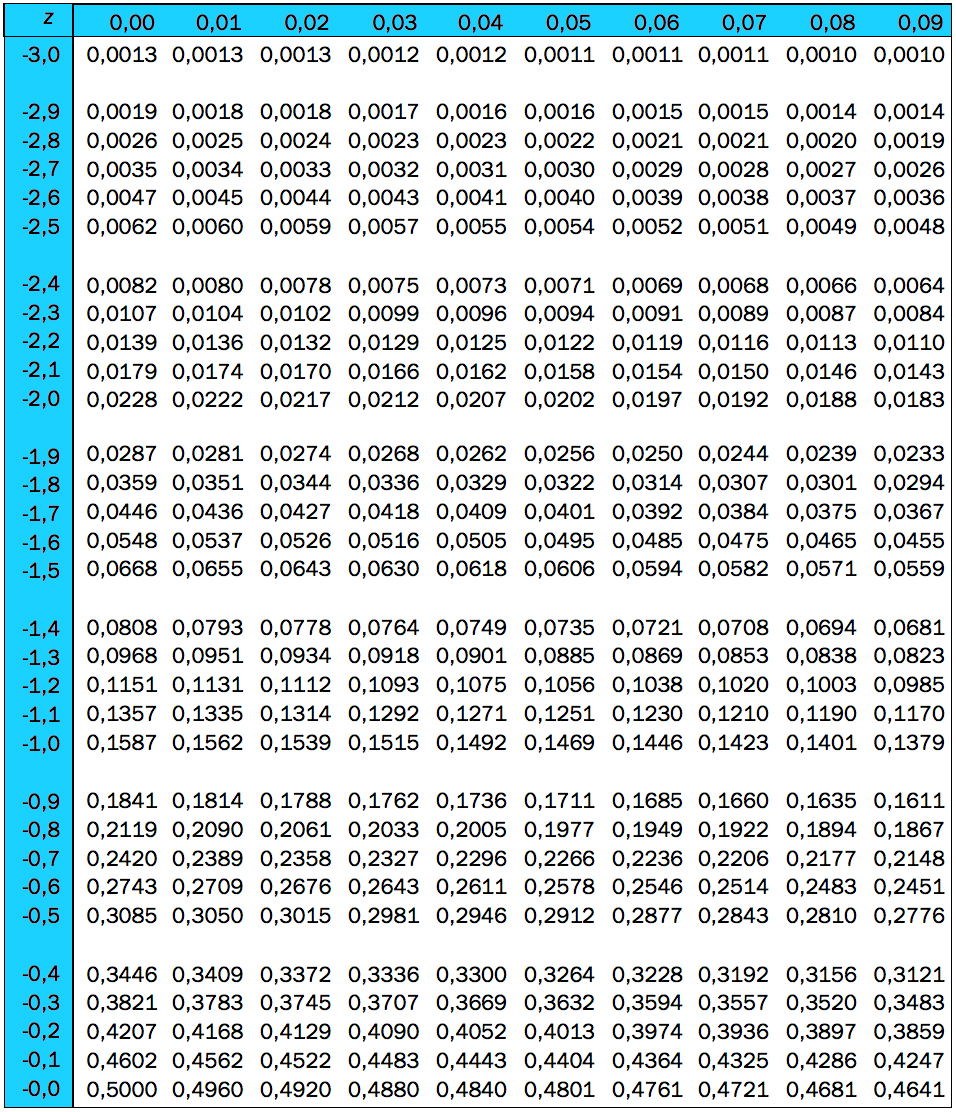
Flott opplegg og undervisning😊
Tusen takk!
Gjorde unna R2 som privatist på et halvt år!! Mattevideo har gjort det mye lettere å fordøye et så tungt pensum på så kort tid. Tusen takk for hjelpa!!😊
Bra undervisning!
Jeg er fornøyd med videone deres det har hjulpet meg til å bestå matten i både Vgs og Uni . Så takk😊
Meget bra!
Tusen takk. Veldig flink lærer. Gode forklaringer.
Helt topp :D
Bra side.
Kjempebra!😊
Bra side. Veldig gode forklaringer😊
Tror dette kommer til å redde meg på noen prøver fremover. Takk! :D
takk for hjelpen
Takk for læreren av denne siden. Det er utrolig en bra side, fikk meg mye. Tusen hjertelig takk
Kan trygt anbefale Arne Hovland! Beste læreren jeg har hatt i løpet av drøyt 20 år med utdanning.
takk for denne siden :D min 1T mattelærer snakker så monotont og gjør matte så kjedelig at interessen svinner vekk og jeg sovner etter 5 minutter.