
1 - 2 - 3 klasse

Lær VGS matten fra A til Å
med de beste metodene


Enkelt å
holde fokus



Forstå det
vanskelige


Få god
oversikt


Øv på
riktig tema


Få hjelp når
du stopper opp



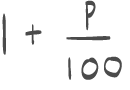
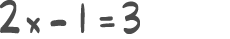
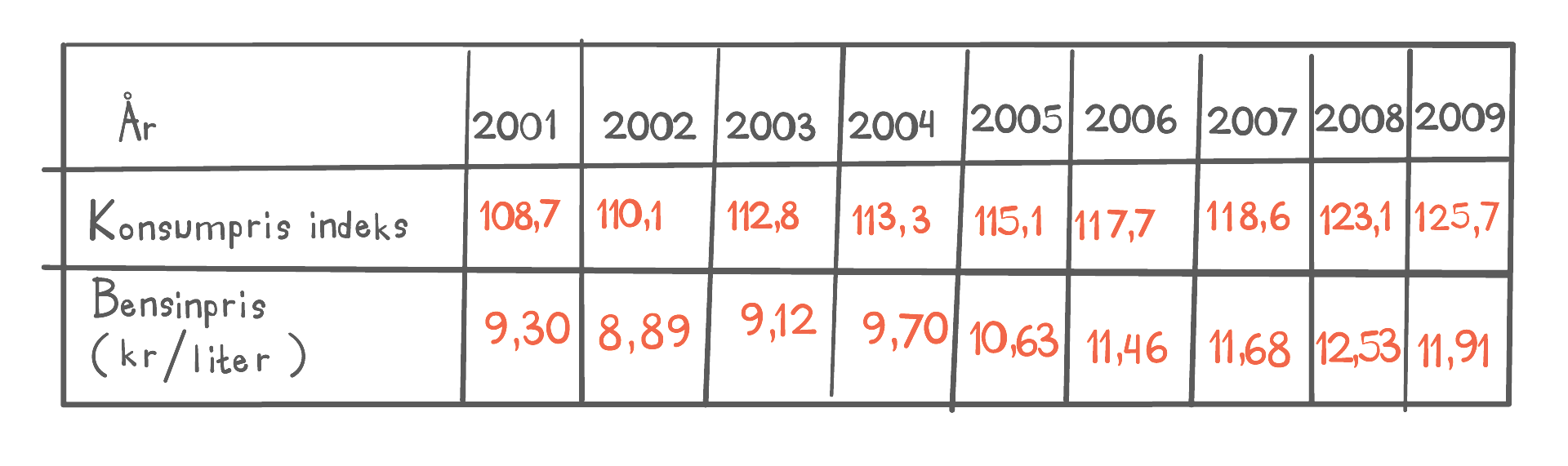
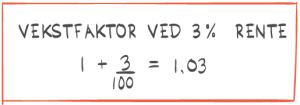

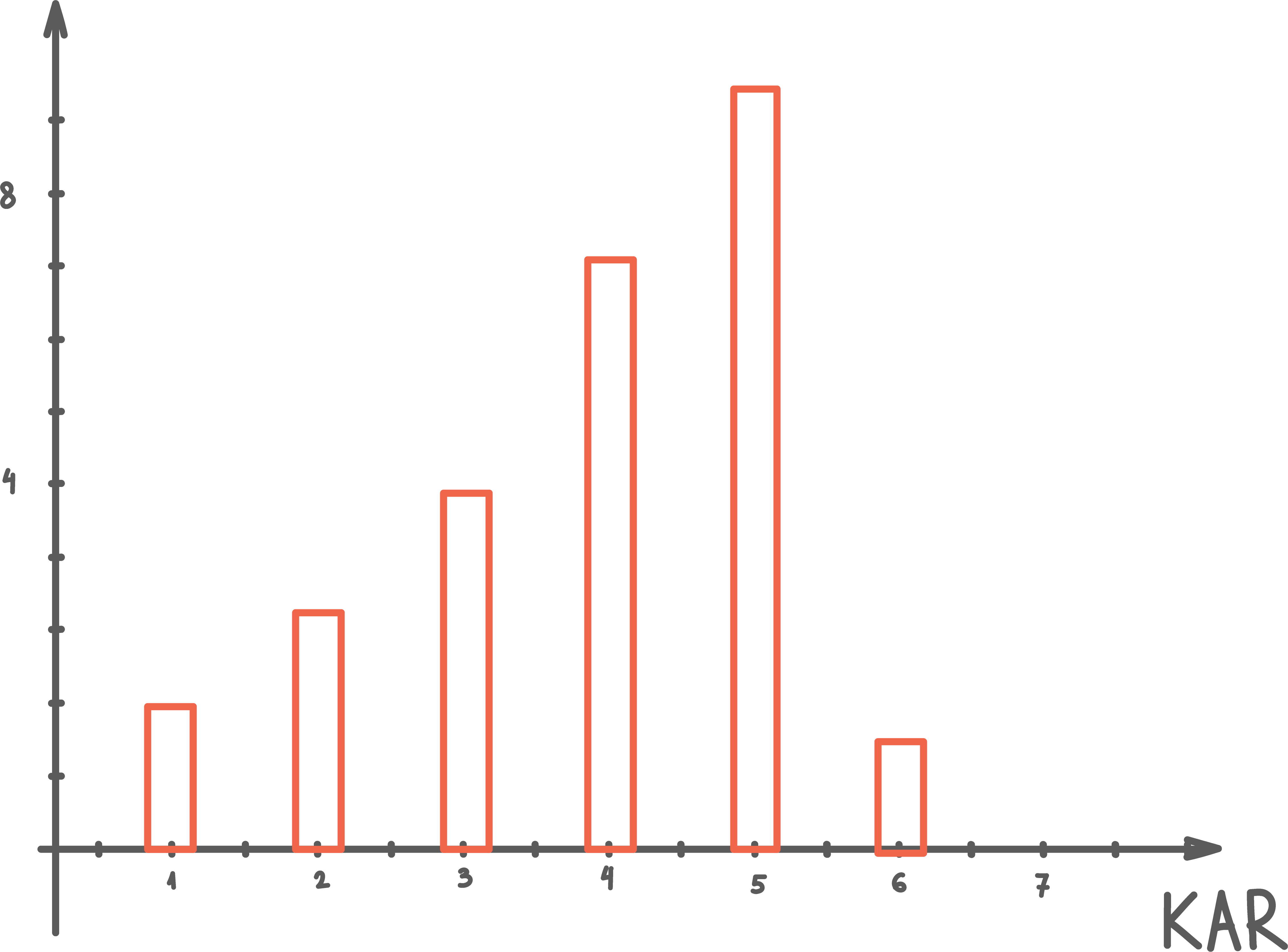
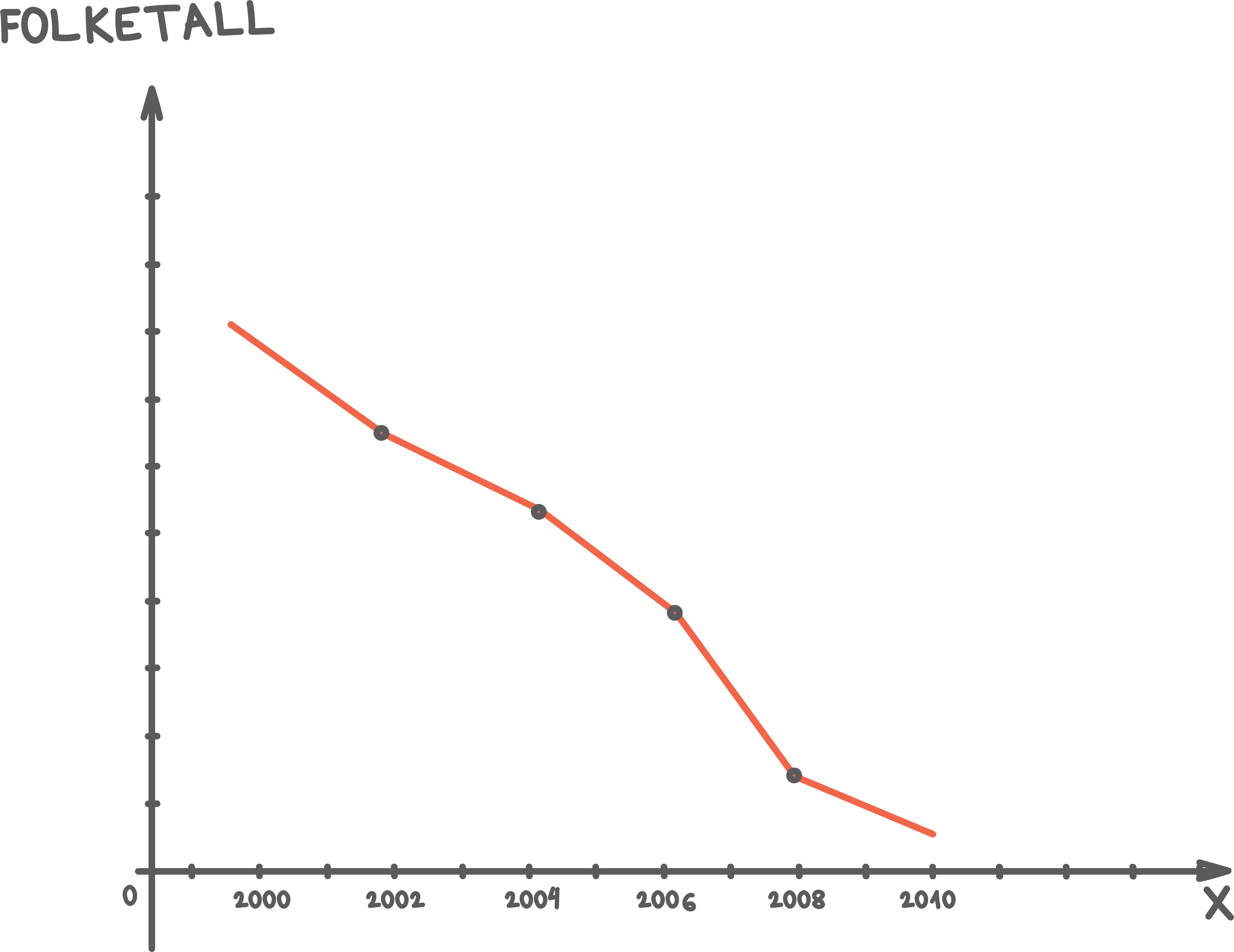
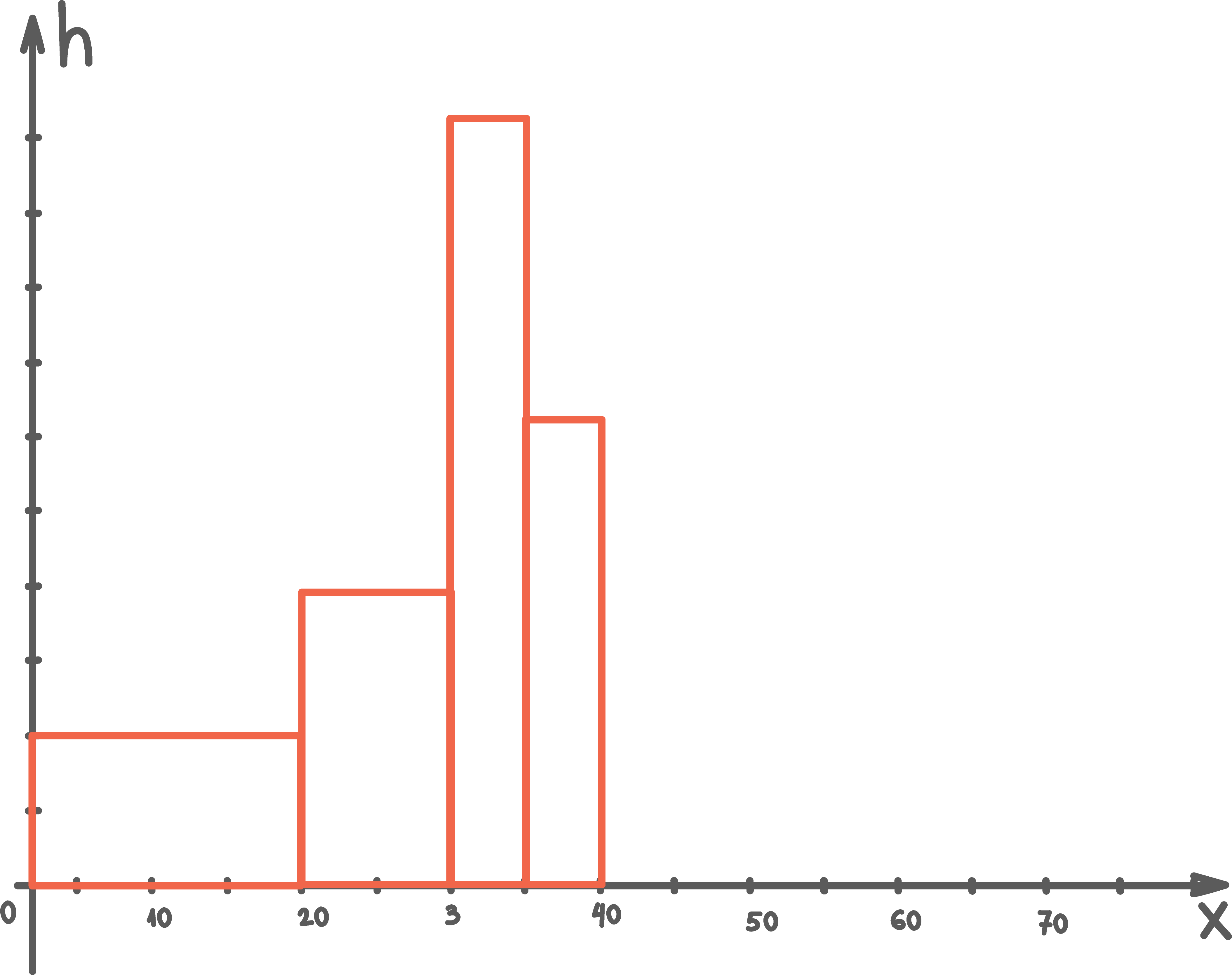



Oppgave 4 (4 poeng)
 a) Bestem gjennomsnittet og medianen for dette datamaterialet.
b) Bestem den kumulative frekvensen for to mål. Hva betyr dette?
a) Bestem gjennomsnittet og medianen for dette datamaterialet.
b) Bestem den kumulative frekvensen for to mål. Hva betyr dette?
Oppgave 5 (2 poeng)
En vare selges i to forskjellige butikker. Prisen er den samme i begge butikkene.- I butikk A settes prisen opp med 20 %.
- I butikk B settes prisen først opp med 10 %, og så etter noen dager med 10 % til.
Oppgave 6 (2 poeng)
Ved en skole er det 120 elever. Elevrådet skal arrangere aktivitetsdag, og elevene kan melde seg på én av fire turer. Elevene fordeler seg slik: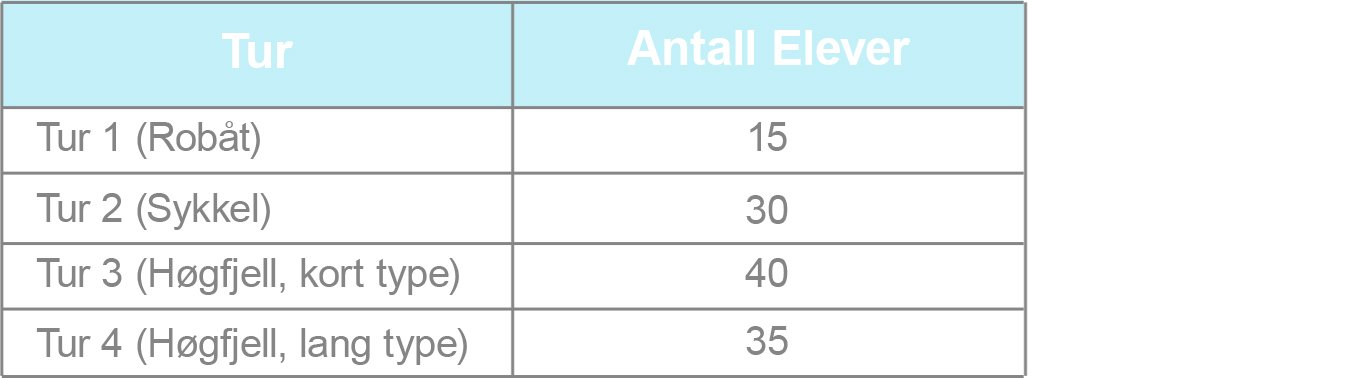 Gjør beregninger og lag et sektordiagram som viser fordelingen. Det skal gå klart fram hvor mange grader hver av sektorene i diagrammet er på.
Gjør beregninger og lag et sektordiagram som viser fordelingen. Det skal gå klart fram hvor mange grader hver av sektorene i diagrammet er på.
Oppgave 7 (2 poeng)
Ved en skole er det 100 elever i Vg1. En lærer har undersøkt hvor mye tid elevene bruker på matematikkleksene i løpet av en uke. Resultatene er gitt i tabellen nedenfor.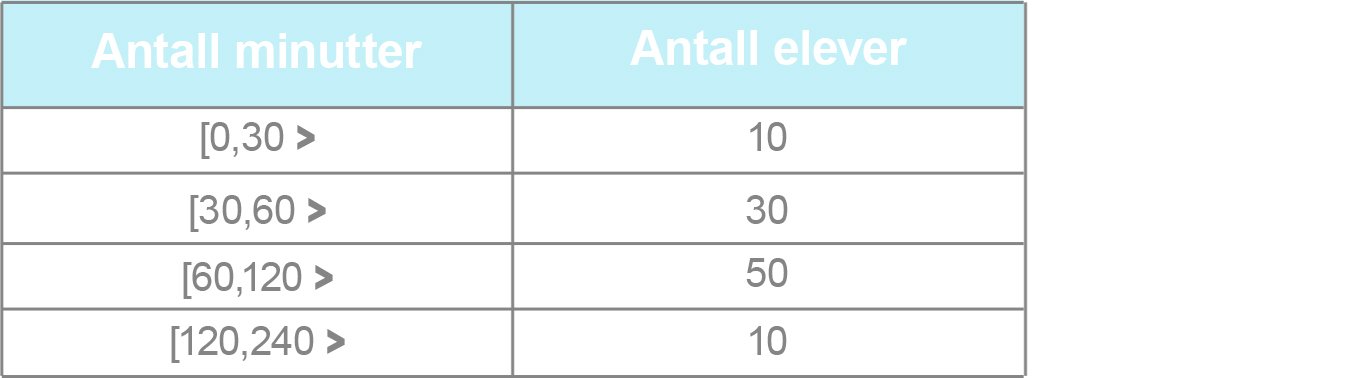 Hvor lang tid bruker en elev i gjennomsnitt på matematikkleksene i løpet av en uke?
Hvor lang tid bruker en elev i gjennomsnitt på matematikkleksene i løpet av en uke?
Oppgave 8 (2 poeng)
Whisky lagres på tønner. En tønne på 500 L fylles opp og blir plassert på lager. Hvert år fordamper omtrent 2 % av innholdet i tønnen.a) Sett opp et uttrykk som du kan bruke til å regne ut hvor mange liter whisky det vil være igjen i tønnen etter 12 år.
b) Sett opp et uttrykk som du kan bruke til å regne ut hvor mange liter whisky som vil ha fordampet fra tønnen etter 20 år.
Oppgave 10 (4 poeng)
Stig har fått en kakeoppskrift fra tante Mathilde i Amerika. I oppskriften står det at kaken skal stekes på 350 °F. Han lurer på hvor mange grader celsius dette tilsvarer. Stig har en gradestokk utenfor kjøkkenvinduet som viser både celsiusgrader og fahrenheitgrader. Se bildet under til høyre.a) Tegn av tabellen nedenfor i besvarelsen din. Bruk gradestokken til høyre, og fyll ut tabellen.
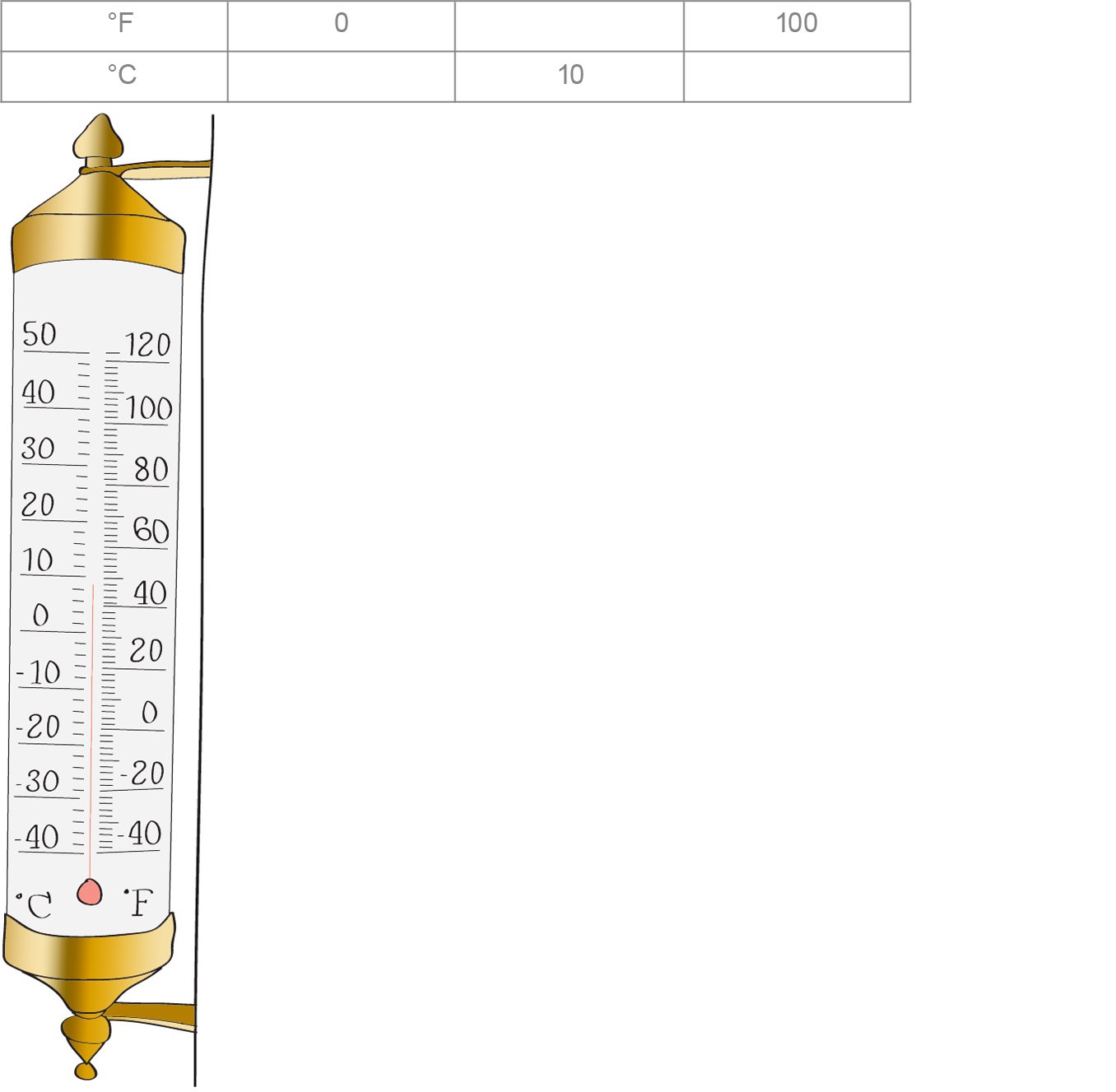
b) Tegn et koordinatsystem med grader fahrenheit langs x- aksen og grader celsius langs y-aksen. Marker verdiene fra tabellen i a) som punkter i koordinatsystemet.
c) Tegn en rett linje som går gjennom punktene. Bruk linjen til å finne ut hvor mange grader celsius Stig skal steke kaken på.

Oppgave 1 (6 poeng)
 Snorre veide 3,1 kg da han ble født. Tabellen nedenfor viser vekten hans, y kg, x dager etter fødselen.
Snorre veide 3,1 kg da han ble født. Tabellen nedenfor viser vekten hans, y kg, x dager etter fødselen.

a) Bruk regresjon til å bestemme en lineær modell for Snorres vekt ut fra datamaterialet i tabellen ovenfor.
b) Hvor lang tid vil det gå før Snorre veier 7,0 kg ut fra modellen i oppgave a)?
En ettåring veier normalt mellom 8,0 kg og 12,0 kg.c) Bruk modellen du fant i oppgave a) til å bestemme Snorres vekt etter 365 dager. Kommenter resultatet.
Oppgave 2 (6 poeng)
 Våren 2012 var klasse 2A og klasse 2B ved en skole oppe til eksamen i matematikk 2P.
Tabellen nedenfor viser hvordan karakterene fordelte seg i de to klassene.
Våren 2012 var klasse 2A og klasse 2B ved en skole oppe til eksamen i matematikk 2P.
Tabellen nedenfor viser hvordan karakterene fordelte seg i de to klassene.
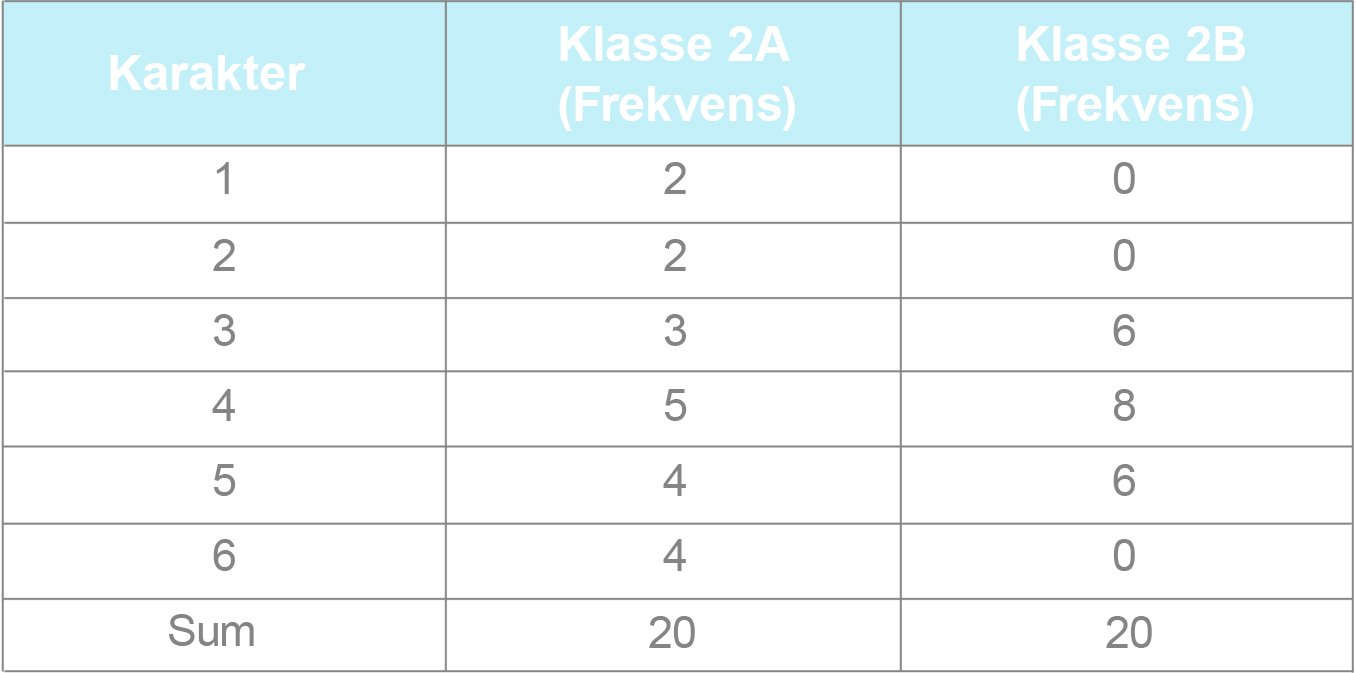 a) Bruk regneark til å lage en grafisk framstilling som viser karakterfordelingen i de to klassene.
b) Bruk regneark til å bestemme gjennomsnittskarakter, mediankarakter og standardavvik for karakterene i hver av de to klassene.
Hva forteller svarene om resultatene i de to klassene?
a) Bruk regneark til å lage en grafisk framstilling som viser karakterfordelingen i de to klassene.
b) Bruk regneark til å bestemme gjennomsnittskarakter, mediankarakter og standardavvik for karakterene i hver av de to klassene.
Hva forteller svarene om resultatene i de to klassene?
Oppgave 3 (5 poeng)
Politiet har gjennomført fartskontroller på to veistrekninger. Den ene veistrekningen har fartsgrense 50 km/h og den andre 80 km/h. Nedenfor ser du resultatene fra hver av de to kontrollene.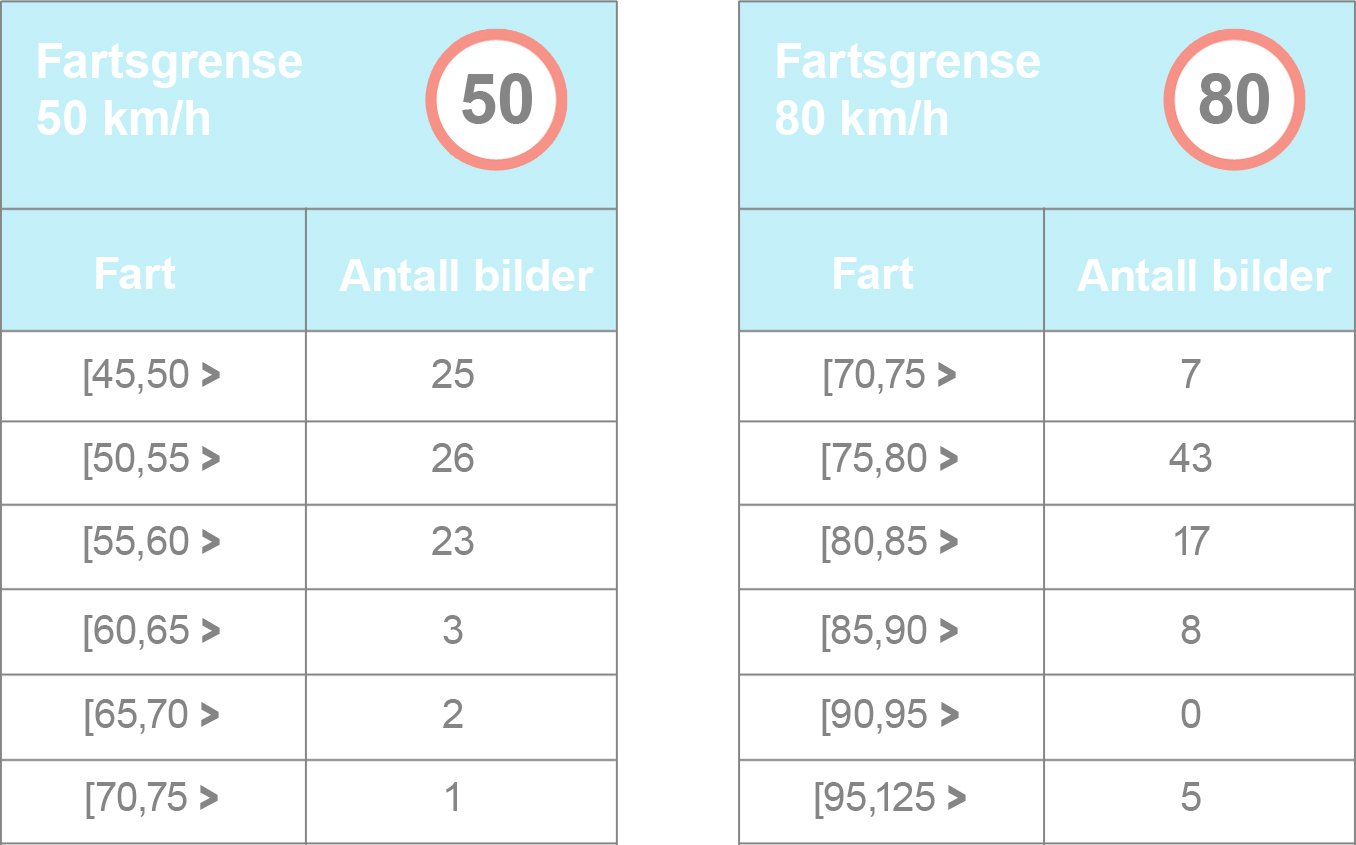 a) Bestem gjennomsnittsfarten til bilene i hver av de to kontrollene.
b) Hvor mange prosent av bilførerne kjørte 10 % eller mer over fartsgrensen i hver av de to kontrollene?
a) Bestem gjennomsnittsfarten til bilene i hver av de to kontrollene.
b) Hvor mange prosent av bilførerne kjørte 10 % eller mer over fartsgrensen i hver av de to kontrollene?
Oppgave 4 (4 poeng)
I en teatersal er det 580 plasser. På første stolrad er det 10 plasser. På andre stolrad er det 12 plasser, og på tredje stolrad er det 14 plasser. Se figuren nedenfor. Slik fortsetter det å øke med to plasser for hver stolrad bakover i salen.
Slik fortsetter det å øke med to plasser for hver stolrad bakover i salen.
a) Hvor mange stolrader er det i salen?
På første stolrad er billettprisen 350 kroner. På stolrad nummer to er billettprisen 340 kroner. Slik går billettprisen ned med 10 kroner for hver stolrad bakover i salen.b) På hvilken stolrad koster billettene mest til sammen?
Oppgave 5 (5 poeng)
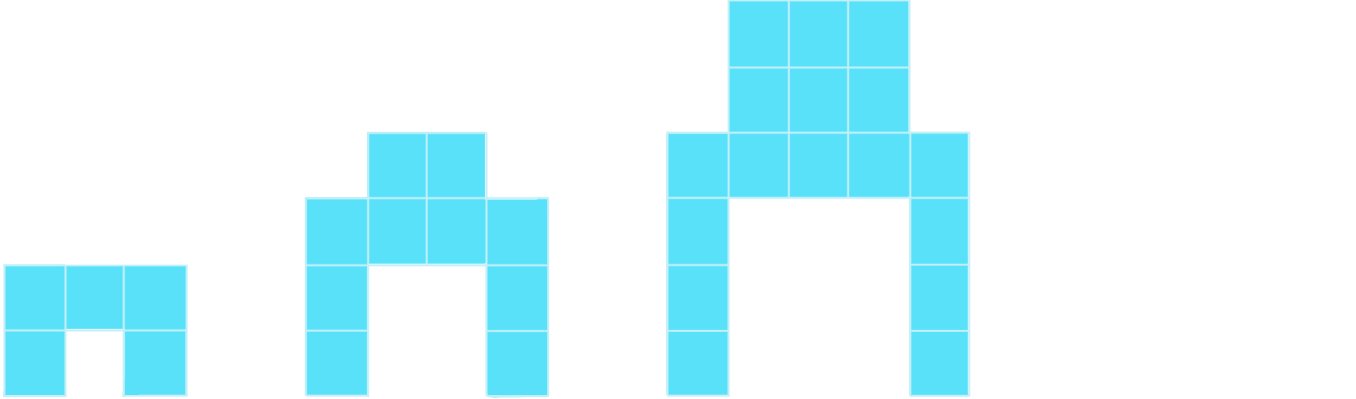 Sondre lager figurer med klosser etter et fast mønster. Ovenfor ser du m1, m2 og m3.
Sondre lager figurer med klosser etter et fast mønster. Ovenfor ser du m1, m2 og m3.
a) Følg samme mønster, og tegn m4. Hvor mange klosser trenger Sondre for å lage m5 og for å lage m6?
b) Sett opp en modell som viser hvor mange klosser Sondre trenger for å lage mn, uttrykt ved n. Bruk modellen til å bestemme hvor mange klosser han trenger for å lage m20.
Oppgave 6 (4 poeng)
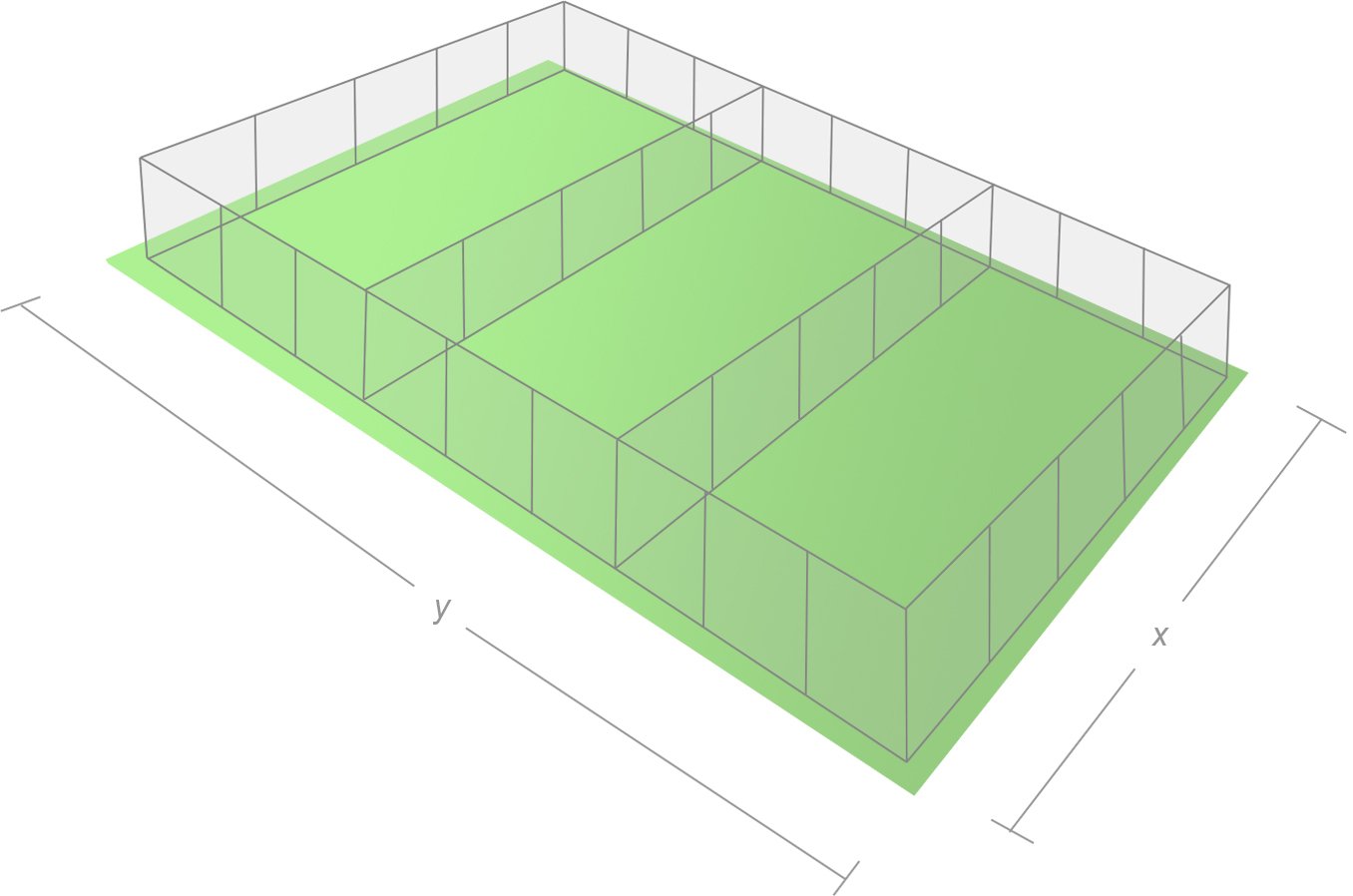 En bonde har 500 m gjerde. Han skal lage et rektangulært område som han skal dele i tre like store deler. Vi setter bredden i rektanglet lik x og lengden lik y. Se figuren ovenfor.
En bonde har 500 m gjerde. Han skal lage et rektangulært område som han skal dele i tre like store deler. Vi setter bredden i rektanglet lik x og lengden lik y. Se figuren ovenfor.
a) Vis at arealet av området er gitt ved
b) Bruk graftegner til å bestemme x slik at arealet av området blir størst mulig. Hvor stort er arealet da?
Oppgave 7 (6 poeng)
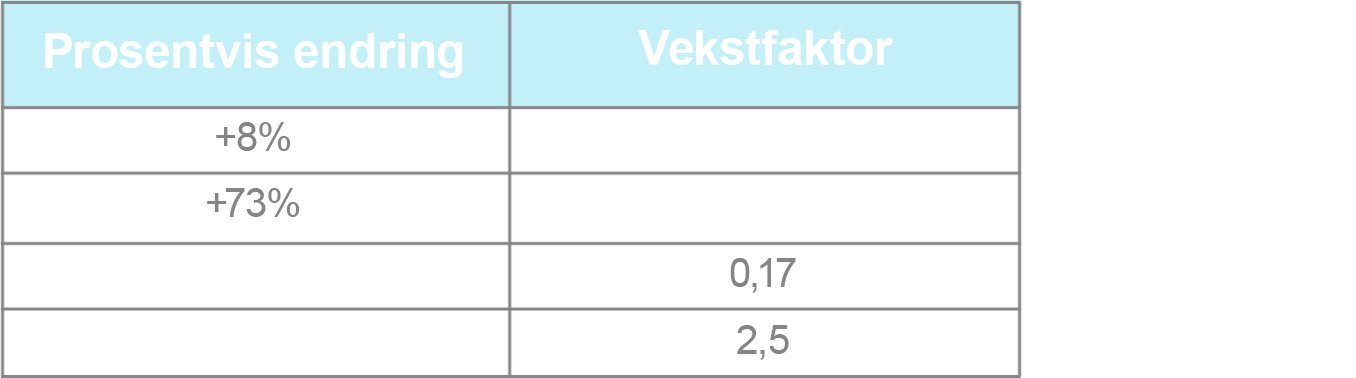
 Vibeke har fått en bakterieinfeksjon og tar tabletter med antibiotika. En tablett inneholder 220 mg antibiotika. Antall milligram antibiotika i kroppen reduseres med 11 % hver time.
Vibeke har fått en bakterieinfeksjon og tar tabletter med antibiotika. En tablett inneholder 220 mg antibiotika. Antall milligram antibiotika i kroppen reduseres med 11 % hver time.
a) Vibeke tar én tablett. Hvor mange milligram antibiotika er det igjen i kroppen hennes etter én time, og hvor mange milligram antibiotika er det igjen i kroppen hennes etter åtte timer?
Vibeke tar en tablett hver åttende time.b) Hvor mange milligram antibiotika har hun i kroppen rett etter at hun har tatt sin andre tablett, og hvor mange milligram antibiotika har hun i kroppen rett etter at hun har tatt sin tredje tablett?
c) Skisser grafen som viser hvor mange milligram antibiotika Vibeke til enhver tid har i kroppen det første døgnet etter at hun begynte å ta tablettene.
Prøvesmak våre videoer
Mattevideo tilbyr fullstendig dekning av kursene 1P, 1PY, 1T, 2P, S1, R1, S2 og R2 innenfor videregående skole. Under har vi lagt ut noen smakebiter fra disse kursene, så du kan sjekke ut noe av det vi har å by på, før du bestemmer deg for å bli abonnent.1P - Polynomfunksjoner1PY - Prosentregning1T - Funksjonsbegrepet2P - Første gradS1 - LikningssettR1 - Å finn den deriverte ved å bruke derivasjonsreglerS2 - Aritmetiske og geometriske rekkerR2 - Sinusfunksjoner og cosinusfunksjoner

Lær å jobbe smarterepå 5 minutter
Det finnes mange ulike studieteknikker, utfordringen er ofte å finne de som fungerer best for deg. I oversikten under finner du enkelt de beste teknikkene.
Alle våre studietips er laget av vår superelev - med 6 i snitt fra vgs. Ingen av artiklene tar mer enn 5 minutter å lese - slik at du kan starte læringen så fort som mulig.
Hva skjer i hjernen når du lærer?
 Du møter noe nytt for første gang
Du møter noe nytt for første gang Du kobler den nye tingen med kunnskap du har fra før
Du kobler den nye tingen med kunnskap du har fra før Du repeter og styrker sammenhengene
Du repeter og styrker sammenhengene Du bruker kunnskapen
Du bruker kunnskapen

Vanlige utfordringer - og hvordan løse dem


Teknikkene som gjør deg til en superelev
La oss ringe deg, så finner vi en god løsning.


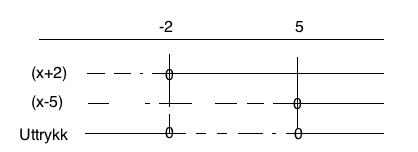
I denne videoen skal vi se på ulikheter. Ulikheter er ganske like ligninger. Forskjellen er at det ikke er et likhetstegn, men et ulikhetstegn. For eksempel x minus to er mindre enn tre x minus én. Vi ser vi har noe på venstresiden og noe på høyresiden, ikke av et likhetstegn, men av ulikhetstegnet, og vi kan bruke stort sett de samme metodene når vi løser ulikheter som når vi løser ligninger.
Spesielt gjelder det førstegradsulikheter som vi har her. Her er det første grad fordi det er x i første og tre x. Det er ikke opphøyd i andre eller tredje eller noe sånt.
Her repeterer vi de reglene som gjelder ligninger, som også kan brukes. Vi kan legge til eller trekke fra det samme tallet på begge sider av ulikhetstegnet. Vi kan gange eller dele med det samme positive tallet på begge sider av ulikhetstegnet. Men her måtte jeg skrive positivt, fordi det er nemlig en egen greie når man ganger eller deler med negative tall, da må vi nemlig snu ulikhetstegnet.
Og det kan vi se på i det første eksempelet her: x minus to er mindre enn tre x minus én. Strategien fra ligninger er å ha x-ene på den ene siden av likhetstegnet og tallene på den andre, så i dette tilfellet blir det da
Vi vil ha x-ene på venstre side i dette eksemplet, så hvis vi trekker fra tre x på begge sider
av ulikhetstegnet.
Så står det på en måte tre x minus én, og så minus tre x da.
Da har vi trukket fra tre x på begge sider, og da forsvinner jo tre x på høyresiden.
Minus to.
Så hvis vi nå plusser på to på begge sider
Så vil jo minus to pluss to bli null, og da har vi med andre ord flyttet to over på høyre side.
Så det er jo det vi gjør når vi har litt dårligere tid, så bare flytter vi leddene fra den ene siden til den andre, men da husker vi å skifte fortegn. Sånn som vi ser her: tre x står det der, og der står det minus tre x. Minus to sto det der, og nå står det pluss to på høyre side, akkurat som i likninger. Men da, når vi trekker sammen, så får vi minus to x er mindre enn
En minus en pluss to er lik en, og da kommer vi til siste skritt, som er å dele på minus to. Og da gjør vi det; vi gjør det ikke akkurat på linja her, vi bare gjør det under. Så da blir det minus to x delt på minus to, men da må vi nemlig snu pila.
En over minus to
Og da får vi x blir større enn minus én.
Ha, så det blir løsningen.
[..]
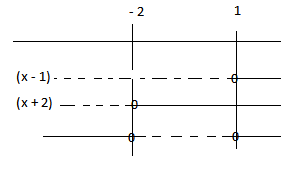
Nå kan vi se på en ulikhet til: x minus to er mindre enn x minus tre.
Samme greia, så vi flytter over, så da får vi x, og så flytter vi den x-en fra høyresiden, da blir det minus x.
Blir mindre enn minus tre, flytter over to.
Men da får vi en litt interessant situasjon, da får vi nemlig null.
x-er er mindre enn
minus én.
Null er mindre enn minus én. Er det riktig at null er mindre enn minus én?
Det er vel ikke riktig det, for minus én er et negativt tall, så det er mindre enn null. Så her har vi fått en situasjon hvor vi får ingen løsning.
Ja, vi har ikke gjort noe galt. Vi har bare kommet fram til at den ulikheten har ingen løsning.
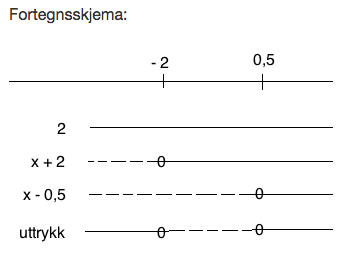
Til slutt kan vi se på et eksempel som egentlig er akkurat det samme som her oppe, bare at her står
Ulikheten på en litt annen måte. Her står høyresiden på venstresiden, og så er pila motsatt.
Det er egentlig akkurat den samme påstanden, at tre x minus én skal være større enn x minus to. Det må jo bety at x minus to skal være mindre enn tre x minus [..] hvis vi nå bruker reglene for
Som jeg har lov å bruke, så kan vi flytte tall over. Så da får vi tre x minus x, da får vi to x. Gjør jeg det litt fortere siden dette er et kjent eksempel.
Flytter over minus én, og da får vi
minus to
pluss én som er minus én
Nå ser vi at vi har et positivt tall
foran x, så da kan vi dele på to, og da trenger vi ikke snu pila. Da blir løsningen x er større enn minus
Det er jo akkurat den samme løsningen som vi fikk i stad, for det var jo akkurat den samme ulikheten. Men vi ser at når vi deler på et positivt tall, da kan vi beholde pilretningen.
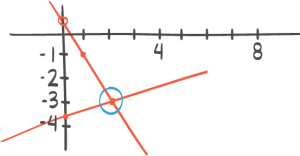
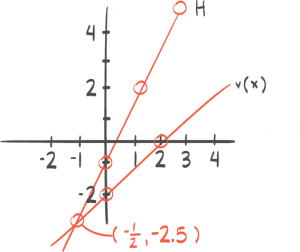
Når det gjelder den løsningen x er større enn minus en halv, så kan vi bare ta en liten kikk på det på en tallinje.
Så da ser vi altså det vi snakker om her. Hvis vi har en tallinje, så kan vi ta med null bare som et sånt referansepunkt. Så ligger minus en halv litt til venstre for null,
og da er altså løsningen på ulikheten alle tall som ligger til høyre for
[..]
Hopp. Noen ganger når vi løser ulikheter, så bruker vi noe som heter løsningsmengde, og da kunne vi jo skrevet det som minus en halv
komma og så pil oppover.
Det betyr alle tall som er større enn minus en halv.
Så den skrivemåten her kan det være greit å se, for det hender du finner den i fasitter, for eksempel.


































Flott opplegg og undervisning😊
Tusen takk!
Gjorde unna R2 som privatist på et halvt år!! Mattevideo har gjort det mye lettere å fordøye et så tungt pensum på så kort tid. Tusen takk for hjelpa!!😊
Bra undervisning!
Jeg er fornøyd med videone deres det har hjulpet meg til å bestå matten i både Vgs og Uni . Så takk😊
Meget bra!
Tusen takk. Veldig flink lærer. Gode forklaringer.
Helt topp :D
Bra side.
Kjempebra!😊
Bra side. Veldig gode forklaringer😊
Tror dette kommer til å redde meg på noen prøver fremover. Takk! :D
takk for hjelpen
Takk for læreren av denne siden. Det er utrolig en bra side, fikk meg mye. Tusen hjertelig takk
Kan trygt anbefale Arne Hovland! Beste læreren jeg har hatt i løpet av drøyt 20 år med utdanning.
takk for denne siden :D min 1T mattelærer snakker så monotont og gjør matte så kjedelig at interessen svinner vekk og jeg sovner etter 5 minutter.