1 - 2 - 3 klasse
Lær VGS matten fra A til Å
med de beste metodene
Enkelt å
holde fokus
Forstå det
vanskelige
Få god
oversikt
Øv på
riktig tema
Få hjelp når
du stopper opp
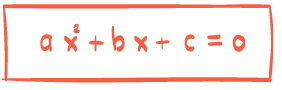
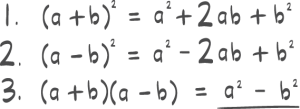
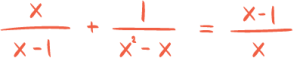
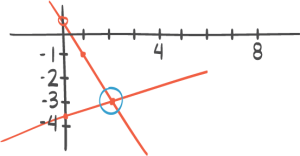
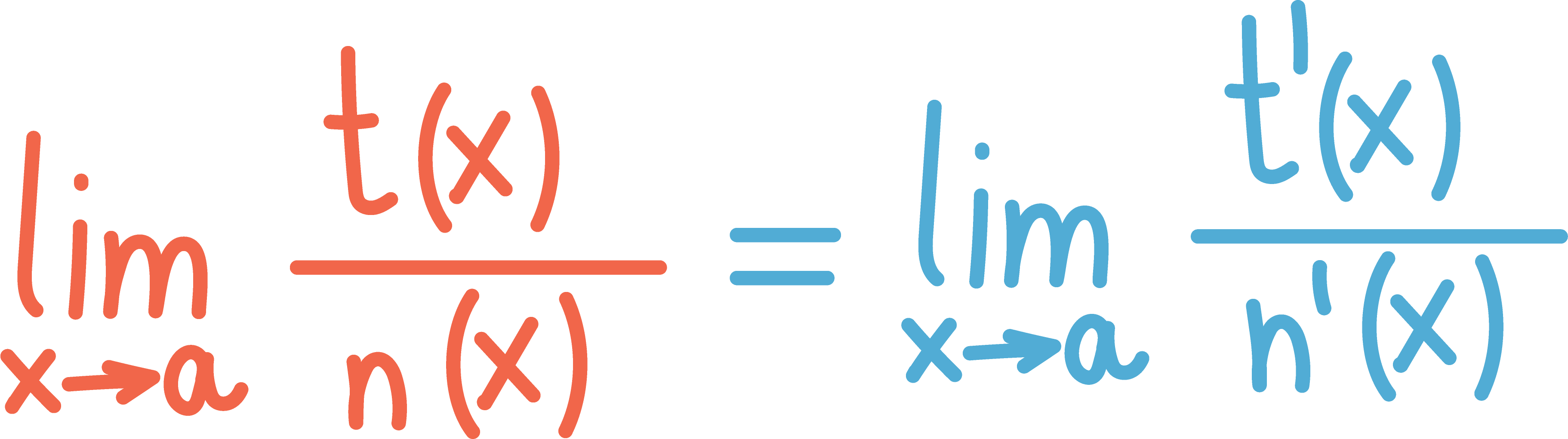
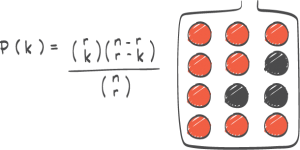
Oppgave 1 (5 poeng)
Løs likningenea)
b)
c)
Oppgave 2 (2 poeng)
Løs likningssystemet
Oppgave 3 (6 poeng)
Skriv så enkelt som muliga)
b)
c)
Oppgave 4 (2 poeng)
Løs ulikheten
Oppgave 5 (5 poeng)
a) Skriv ned de åtte første radene i Pascals talltrekant.
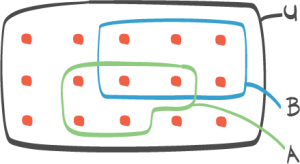
I en eske ligger det 3 røde og 4 blå kuler. Tenk deg at du skal trekke tilfeldig 3 kuler uten tilbakelegging.b) Bestem sannsynligheten for at du trekker tre blå kuler.
c) Bestem sannsynligheten for at det er både røde og blå kuler blant de tre kulene du trekker.
Oppgave 6 (2 poeng)
Skraver området som er avgrenset av ulikhetene nedenfor, i et koordinatsystem.
Oppgave 7 (4 poeng)
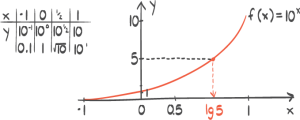
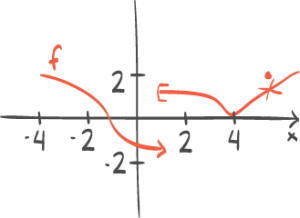
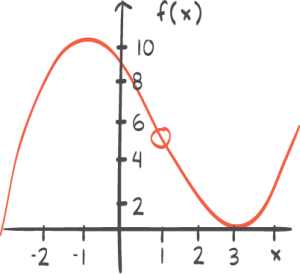
Funksjonen f er gitt veda) Lag en skisse av grafen til f . b) Løs likningen
Oppgave 8 (7 poeng)
Funksjonen g er gitt veda) Bestem b) Bestem toppunktet og bunnpunktet på grafen til g. c) Bestem den gjennomsnittlige vekstfarten til g i intervallet [0, 2]. d) Bestem de punktene på grafen der den momentane vekstfarten er 24.
Oppgave 9 (3 poeng)
Nedenfor ser du fortegnslinjen til , for en funksjon f.
Oppgave 1 (3 poeng)
Einar er fiskehandler. Han selger torsk og sei. En dag solgte han 110 kg torsk og 200 kg sei. Han fikk 6795 kroner. Dagen etter solgte han 150 kg torsk og 230 kg sei. For dette fikk han 8390 kroner. Sett opp et likningssystem, og bruk CAS til å bestemme hvilken pris Einar fikk per kilogram for torsken, og hvilken pris han fikk per kilogram for seien.Oppgave 2 (6 poeng)
Et flyselskap har en flyrute mellom Oslo og Bergen. Flyene som brukes, har plass til 116 passasjerer. Sannsynligheten for at en passasjer som har kjøpt billett, ikke møter til flyavgang, er 6 %. Vi lar X være antall passasjerer som møter til en tilfeldig valgt flyavgang.a) Hva må vi forutsette for å kunne bruke en binomisk sannsynlighetsmodell i denne situasjonen?
I resten av denne oppgaven går vi ut fra at X er binomisk fordelt.b) Til en flyavgang er det solgt 122 billetter. Bestem sannsynligheten for at alle som møter, får plass på flyet.
Flyselskapet ønsker at sannsynligheten skal være minst 95 % for at alle som møter, skal få plass på flyet.c) Hvor mange billetter kan flyselskapet maksimalt selge da?
Oppgave 3 (7 poeng)
Frode og Peter lager to typer fuglekasser. Type A er for meiser, og type B er for ugler. Frode lager delene til kassene, mens Peter setter dem sammen og maler dem.- Frode bruker 10 minutter på å lage delene til en kasse av type A og 30 minutter på å lage delene til en kasse av type B.
- Peter bruker 20 minutter på å sette sammen og male en kasse av type A og 30 minutter på en kasse av type B.
- I løpet av en uke kan Frode jobbe 15 timer.
- I løpet av en uke kan Peter jobbe 20 timer.
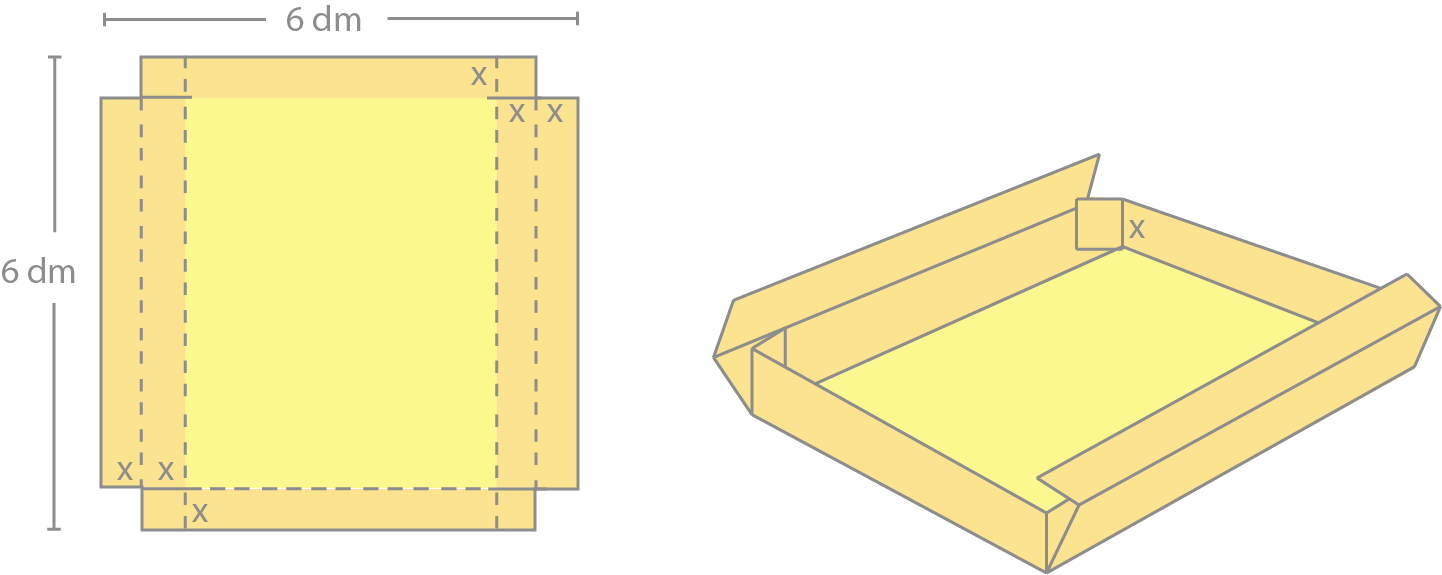
a) Forklar at x og y må ligge i området som er avgrenset av ulikhetene nedenfor:
b) Skraver dette området i et koordinatsystem.
Når de selger fuglekassene, har de en fortjeneste på 60 kroner for en kasse av type A og 150 kroner for en kasse av type B.c) Hvor mange kasser bør de produsere av hver type for at fortjenesten skal bli størst mulig?
Etterspørselen etter fuglekasser av begge typer er veldig stor, så Frode sier han kan jobbe 3 timer ekstra en uke.d) Hvor mange kasser bør de produsere av hver type denne uken dersom de vil ha størst mulig fortjeneste?
Oppgave 4 (8 poeng)
Arne har sommerjobb som montør i en bedrift som produserer en bestemt type pumper. Han har lagt merke til at arbeidstempoet endrer seg i løpet av dagen. En dag teller han opp annenhver time hvor mange pumper han har montert så langt den dagen. Tabellen nedenfor viser resultatet
a) Bruk regresjon til å lage et tredjegradspolynom g som kan brukes som modell for hvor mange pumper Arne setter sammen i løpet av de x første timene på jobb en dag.
I resten av oppgaven lar vi funksjonen f gitt vedvære en modell for antall pumper Arne klarer å montere i løpet av de x første timene på jobb en dag.
b) Bruk graftegner til å tegne grafen til f i et koordinatsystem.
Arne kan velge om han vil ha 9 kroner per pumpe han monterer, eller 190 kroner per time han jobber.c) Hvor mange timer må han jobbe på én dag for at det skal lønne seg å velge betaling per montert pumpe?
d) Hvor mange timer må han jobbe én dag for at forskjellen på lønn per pumpe og lønn per time skal bli størst mulig?
Prøvesmak våre videoer
Mattevideo tilbyr fullstendig dekning av kursene 1P, 1PY, 1T, 2P, S1, R1, S2 og R2 innenfor videregående skole. Under har vi lagt ut noen smakebiter fra disse kursene, så du kan sjekke ut noe av det vi har å by på, før du bestemmer deg for å bli abonnent.1P - Polynomfunksjoner1PY - Prosentregning1T - Funksjonsbegrepet2P - Første gradS1 - LikningssettR1 - Å finn den deriverte ved å bruke derivasjonsreglerS2 - Aritmetiske og geometriske rekkerR2 - Sinusfunksjoner og cosinusfunksjoner
Lær å jobbe smarterepå 5 minutter
Det finnes mange ulike studieteknikker, utfordringen er ofte å finne de som fungerer best for deg. I oversikten under finner du enkelt de beste teknikkene.
Alle våre studietips er laget av vår superelev - med 6 i snitt fra vgs. Ingen av artiklene tar mer enn 5 minutter å lese - slik at du kan starte læringen så fort som mulig.
Hva skjer i hjernen når du lærer?
Du møter noe nytt for første gang
Du kobler den nye tingen med kunnskap du har fra før
Du repeter og styrker sammenhengene
Du bruker kunnskapen
Vanlige utfordringer - og hvordan løse dem
Teknikkene som gjør deg til en superelev
La oss ringe deg, så finner vi en god løsning.
Ønsker du mer repetisjon av likninger? Sjekk ut 1T.
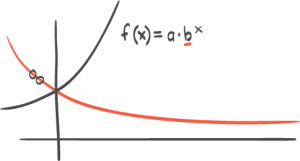
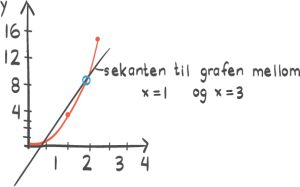
Videre er kostnaden K ved å produsere x enheter git ved K(x)=10 000 + 20x. Vi antar at antall produserte enheter er lik antall solgte enheter.
b) Hvilken pris gir størst overskudd?
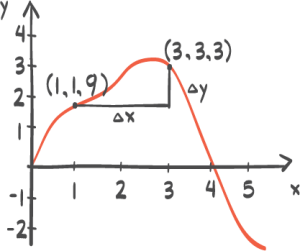
Finn den gjennomsnittlige vekstfarten i periodene
a) [0,5] b) [5,10] c) [10,15]
a) Tolk tallene 25 og 50.
b) Hva var prisen for en tur på 4,3 km?
c) Hvor langt kommer du for 300 kr?
a) Undersøk om f(x) er delelig med: 1) (x-1), 2) (x+1), 3) (x-2)
b) Faktoriser f(x) .
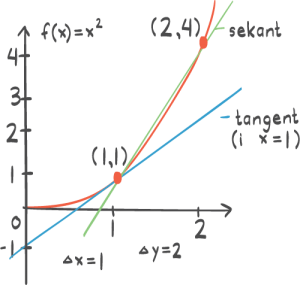
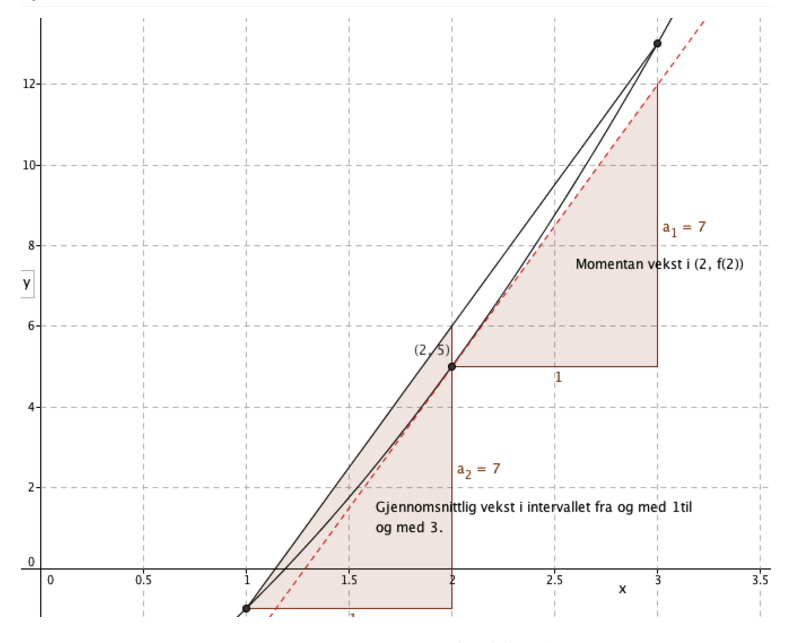
a) Tegn grafen for x mellom -2 og 2
b) Finn gjennomsnittlig vekstfaktor mellom x-verdiene 0 og 2.
c) Finn den momentane vekstfarten i x = 0 grafisk.
d) Finn den momentane vekstfarten i x = 1 grafisk.
a) Hva forteller funksjonsuttrykket?
b) Finn nullpunktet til funksjonen. Hva forteller dette?
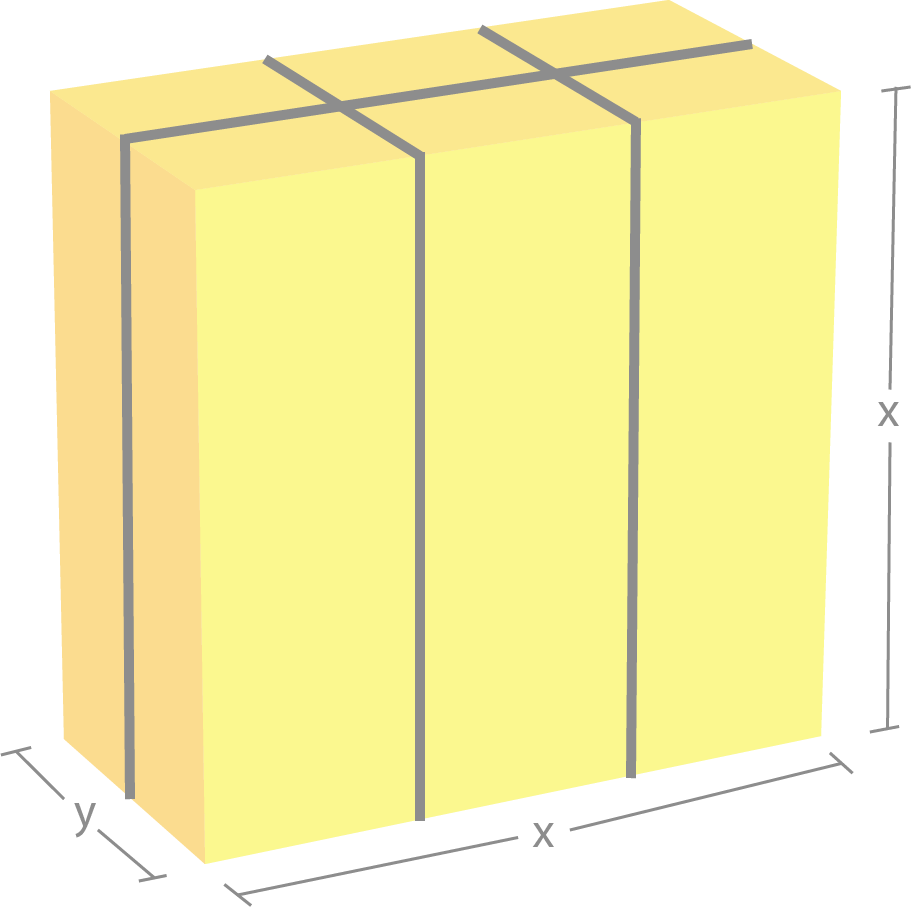
a) Skriv funksjonsuttrykket for h(x).
b) Finn definisjonsmengden og verdimengden for h.
En funksjon f er deriverbar og dobbelderiverbar for alle x.
Nedenfor er det gitt noen utsagn. Skriv av utsagnene. I boksen mellom utsagnene skal du sette inn et av symbolene eller .
a) Grafen til f har et toppunkt i (2, f(2)).
b) og f\'\'(3)>0 Grafen til f har et bunnpunkt i (3, f(3))
Riktig svar!
Ved å vite at f\'(3) = 0, vet vi at det er et ekstremalpunkt i x = 3. Når da f\'\'(3) > 0 i tillegg så vet vi at det er et bunnpunkt.
Riktig svar!
Siden Oslo er i Norge. Man kan ikke bo i Oslo, men ikke i Norge.
En funksjon f er deriverbar og dobbelderiverbar for alle x.
Nedenfor er det gitt noen utsagn. Skriv av utsagnene. I boksen mellom utsagnene skal du sette inn et av symbolene eller .
a) Grafen til f har et toppunkt i (2, f(2)).
Riktig svar!
Siden f\'(2) = 0 kan bety at grafen har et bunnpunkt eller terrassepunkt også, så vil det bare gå én vei.
Riktig svar!
Denne er viktig å bare kunne.
Riktig svar!
Siden e nullerer ln, blir dette som å først gange med 2 så dele på 2. Man kommer tilbake der man startet.
Riktig svar!
Stigningstallet er .
En bedrift produserer en vare. De regner med at kostnadene K ved å produsere x enheter av varen per dag er
,
a) Bestem den gjennomsnittlige vekstfarten til K i intervallet . Hva forteller dette svaret oss?
b) Bestem K\'(100). Hva forteller dette svaret oss?
Bedriften selger varen for 60 kroner per enhet til en butikk som kjøper alt bedriften klarer å produsere.
c) Hvor mange enheter må bedriften produsere per dag for å få størst mulig overskudd?
Riktig svar!
Gjennomsnittlig vekstfart i intervallet null til hundre:
Den gjennomsnittlige vekstfarten i intervallet er 40. Det betyr at kostnadene ved å produsere en enhet mere øker med 40.
Riktig svar!
Riktig svar!
Den lineære går da bare gjennom det ene punktet.
Riktig svar!
Riktig svar!
Ja, fordi her er x en eksponent i funksjonen.
Løs likningen
Riktig svar!
Fra dette ser vi at , eller at: . Når vi løser dette:
Som gir oss: eller
Løs likningen
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Funksjonen f er gitt ved
a) Bestem den momentane vekstfarten til f i punktet (2,f(2)) og den gjennomsnittlige vekstfarten til f i intervallet [ 1, 3 ] .
b) Bestem den momentane vekstfarten til f i punktet (a, f(a)) og den gjennomsnittlige vekstfarten til f i intervallet [a-1,a+1]. Tallet a er en konstant. Sammenlign svarene og kommenter.
Man får samme resultat som i a, men nå rent generelt for x = a.
Funksjonen f er gitt ved
a) Bestem den momentane vekstfarten til f i punktet (2,f(2)) og den gjennomsnittlige vekstfarten til f i intervallet [ 1, 3 ] .
b) Bestem den momentane vekstfarten til f i punktet (a, f(a)) og den gjennomsnittlige vekstfarten til f i intervallet [a-1,a+1]. Tallet a er en konstant. Sammenlign svarene og kommenter.
Man observerer at den momentane vekstfarten i (2,f(2)) er lik den gjennomsnittlige vekstfarten i intervallet [1,3].
Funksjonen er gitt ved
a) Bestem . Hva forteller dette tallet deg?
b) Begrunn at grafen til kun har tangenter med positivt stigningstall.
Funksjonen har momentan vekstfart lik 15 for to x-verdier.
c) Bestem disse x-verdiene.
Det at den momentane vekstfarten er 15 vil si at den deriverte er 15.
\begin{align} f\'(x) &= 15 \\\ 3x^2 + 3 &= 15 \\\ 3x^2 &= 12 \\\ x^2 &= 4 \\\ x &= \pm 2 \end{align}
Funksjonen har en momentan vekstfart på 15 når
og når
Vi skal lage en pakke med form som et rett prisme. Pakken har bredde lik y cm, lengde lik x cm og høyde lik x cm. Vi vil sikre pakken med svart pakkebånd. Se figuren nedenfor.
Vi ser at lengden av pakkebåndet er 8x+4y. Vi vil lage pakken slik at den har størst mulig volum når vi bruker akkurat 900 cm med pakkebånd.
a) Vis at volumet V(x) av pakken kan skrives som
b) Bestem x og y slik at volumet av pakken blir størst mulig. Kommenter svaret ditt. Bestem det største volumet, målt i kubikkdesimeter .
Volum av prisme:
Som skulle vises.
Vi skal lage en pakke med form som et rett prisme. Pakken har bredde lik y cm, lengde lik x cm og høyde lik x cm. Vi vil sikre pakken med svart pakkebånd. Se figuren nedenfor.
Vi ser at lengden av pakkebåndet er 8x+4y. Vi vil lage pakken slik at den har størst mulig volum når vi bruker akkurat 900 cm med pakkebånd.
a) Vis at volumet V(x) av pakken kan skrives som
b) Bestem x og y slik at volumet av pakken blir størst mulig. Kommenter svaret ditt. Bestem det største volumet, målt i kubikkdesimeter .
V \' (x) = -6x^2 + 450x \\\ V\'(x)=0 \\\ -6x^2+450x=0 \\\ x=0 \vee x= 75
Størst volum får pakken når x= 75 centimeter. Da er cm. Man ser at volumet av pakken blir størst når alle sidene i prismet er like lange.
En bedrift lager esker av kvadratiske pappstykker med side lik 6 dm. Dette gjør de ved å klippe ut hjørner som vist nedenfor og brette langs de stiplede linjene.
a) Forklar at volumet V , målt i kubikkdesimeter, til hver eske er gitt ved
,
b) Bruk CAS til å bestemme x slik at volumet blir størst mulig. Bestem dette største volumet
Bedriften skal også lage andre esker der de bruker kvadratiske pappstykker med side lik a dm. De klipper og bretter på samme måte som ovenfor.
c) Bruk CAS til å vise at det maksimale volumet til disse eskene er
Deriverer V ved hjelp av CAS. finner nullpunkt. Størst volum får man når x er 0,63 dm, 6,3 cm. Da er volumet ca. , eller 10,4 liter.
En bedrift lager esker av kvadratiske pappstykker med side lik 6 dm. Dette gjør de ved å klippe ut hjørner som vist nedenfor og brette langs de stiplede linjene.
a) Forklar at volumet V , målt i kubikkdesimeter, til hver eske er gitt ved
,
b) Bruk CAS til å bestemme x slik at volumet blir størst mulig. Bestem dette største volumet
Bedriften skal også lage andre esker der de bruker kvadratiske pappstykker med side lik a dm. De klipper og bretter på samme måte som ovenfor.
c) Bruk CAS til å vise at det maksimale volumet til disse eskene er
Både a og x er positive verdier i denne praktiske oppgaven. Vi ser at linje 5 gir oss det maksimale volumet vi ble bedt om å vise.
Silje driver butikk. I slutten av mars opprettet hun en side på Facebook.
I slutten av april fant Silje ut at antall personer som hadde klikket «liker» på siden hennes x dager etter 31. mars,tilnærmet var gitt ved funksjonen
Her svarer til 31. mars, til 1.april, til 2 . april, og så videre.
Anta at denne funksjonen også vil gjelde for mai
a) Hvor mange personer hadde klikket «liker» på Siljes side før 1. april? Hvor mange prosent øker antall «liker» med per dag ?
b) Vil antall «liker» passere 1000 innen utgangen av mai ?
c) Bestem
Hva forteller disse verdiene om antall «liker» på Siljes side?
80 personer, ettersom .
1,045 tilsvarerer en vekst på 4,5%.
Svaret blir da 80 personer og 4,5% vekst.
Silje driver butikk. I slutten av mars opprettet hun en side på Facebook.
I slutten av april fant Silje ut at antall personer som hadde klikket «liker» på siden hennes x dager etter 31. mars,tilnærmet var gitt ved funksjonen
Her svarer til 31. mars, til 1.april, til 2 . april, og så videre.
Anta at denne funksjonen også vil gjelde for mai.
a) Hvor mange personer hadde klikket «liker» på Siljes side før 1. april? Hvor mange prosent øker antall «liker» med per dag ?
b) Vil antall «liker» passere 1000 innen utgangen av mai ?
c) Bestem
Hva forteller disse verdiene om antall «liker» på Siljes side?
f(16) forteller hvor mange "likes" det var 16. april, 162.
f\'(16) forteller om den momentane endringen denne dagen, en økning på ca 7 "likes".
Flott opplegg og undervisning😊
Tusen takk!
Gjorde unna R2 som privatist på et halvt år!! Mattevideo har gjort det mye lettere å fordøye et så tungt pensum på så kort tid. Tusen takk for hjelpa!!😊
Bra undervisning!
Jeg er fornøyd med videone deres det har hjulpet meg til å bestå matten i både Vgs og Uni . Så takk😊
Meget bra!
Tusen takk. Veldig flink lærer. Gode forklaringer.
Helt topp :D
Bra side.
Kjempebra!😊
Bra side. Veldig gode forklaringer😊
Tror dette kommer til å redde meg på noen prøver fremover. Takk! :D
takk for hjelpen
Takk for læreren av denne siden. Det er utrolig en bra side, fikk meg mye. Tusen hjertelig takk
Kan trygt anbefale Arne Hovland! Beste læreren jeg har hatt i løpet av drøyt 20 år med utdanning.
takk for denne siden :D min 1T mattelærer snakker så monotont og gjør matte så kjedelig at interessen svinner vekk og jeg sovner etter 5 minutter.