
1 - 2 - 3 klasse

Lær VGS matten fra A til Å
med de beste metodene


Enkelt å
holde fokus



Forstå det
vanskelige


Få god
oversikt


Øv på
riktig tema


Få hjelp når
du stopper opp

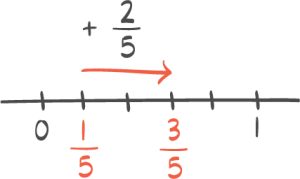

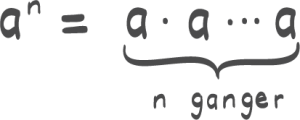

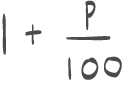
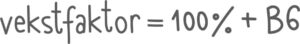

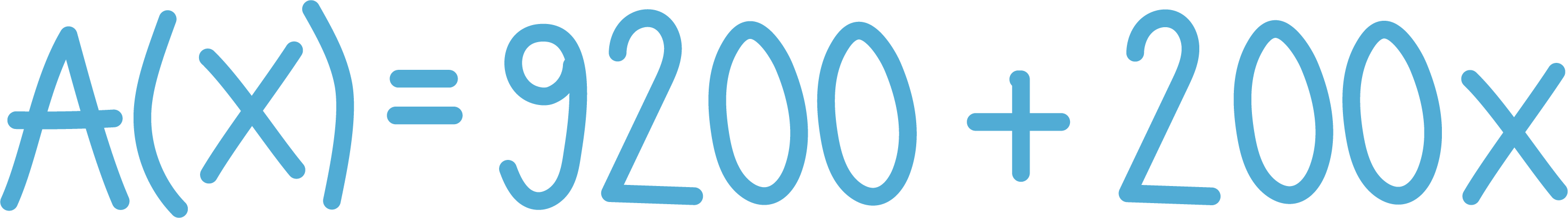




Se gjennom eksamen
Oppgave 1 (3 poeng)
Nedenfor ser du hvor stor oppslutning Kristelig Folkeparti hadde ved stortingsvalgene i 2013 og 2017.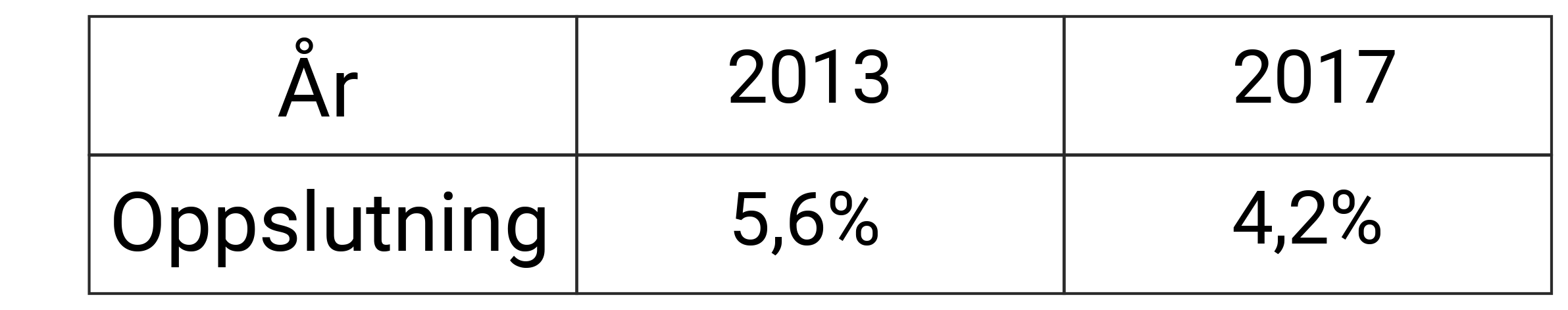
Oppgave 2 (2 poeng)
I en oppskrift står det at du trenger 4 dL melk og 500 g hvetemel for å lage 12 boller. Tenk deg at du har 1 L melk og 1,5 kg hvetemel. Hvor mange boller kan du lage dersom du følger oppskriften?Oppgave 3 (2 poeng)
I 2013 var indeksen for en vare 80. Varen kostet da 1000 kroner. I 2017 var indeksen for den samme varen 120. Hvor mye kostet varen i 2017 dersom prisen har fulgt indeksen?Oppgave 4 (2 poeng)
På et kart er avstanden mellom to byer 9 cm. I virkeligheten er avstanden 45 km. Bestem målestokken til kartet.Oppgave 5 (4 poeng)
Mads skal ta førerkortet for bil. Ved trafikkskolen koster det 13 000 kroner for den obligatoriske delen av føreropplæringen inkludert gebyrer. I tillegg koster det 600 kroner for hver kjøretime. a) Bestem en funksjon K som viser prisen K(x) kroner for å ta førerkortet dersom Mads bruker x kjøretimer. b) Tegn grafen til K i et koordinatsystem. c) Avgjør om prisen for å ta førerkortet og antall kjøretimer er proporsjonale størrelser.Oppgave 6 (2 poeng)
En fire år gammel moped koster i dag 8000 kroner. Mopedens verdi har avtatt med 12 % per år siden den var ny. Forklar hvilket av uttrykkene nedenfor som kan brukes til å finne hvor mye mopeden kostet da den var ny.- 8000−8000⋅0,124
- 8000⋅0,884
- 0,8848000
- 8000⋅0,12−4
Oppgave 7 (3 poeng)

- Terningene viser samme antall øyne.
- Summen av antall øyne er 5 eller mindre.
Oppgave 8 (2 poeng)
Åpningen i toppen av en brusflaske har form som en sirkel med diameter 22 mm. Avgjør om et kronestykke med omkrets 66 mm kan puttes ned i flasken.Oppgave 9 (4 poeng)
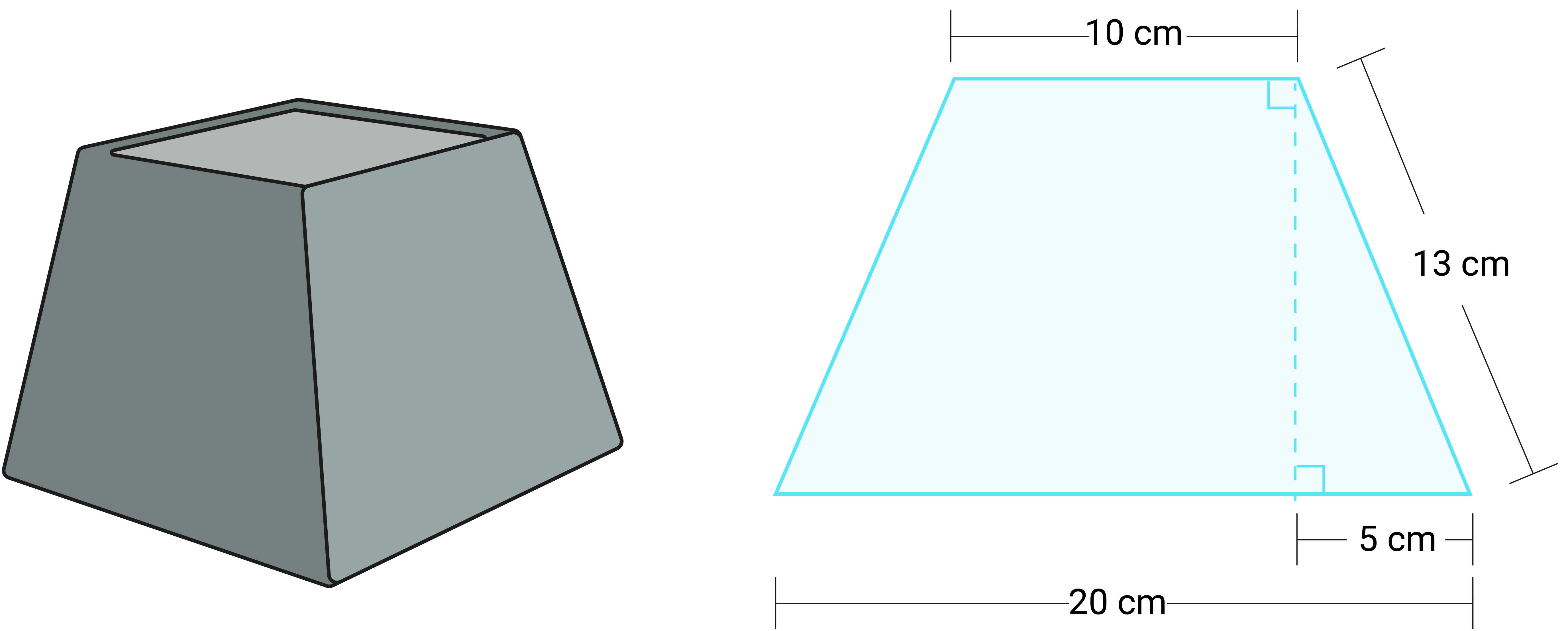
Oppgave 1 (6 poeng)
Oppgave 2 (4 poeng)
Silje har en timelønn på 210 kroner. Hun betaler 2 % av bruttolønnen i pensjonsavgift og har et skattetrekk på 32 %. En måned arbeidet hun 162,5 timer. a) Hvor mye fikk Silje utbetalt denne måneden? I 2017 fikk Silje utbetalt 47 736 kroner i feriepenger. Dette tilsvarer 12,0 % av feriepengegrunnlaget for 2017. b) Bestem feriepengegrunnlaget til Silje for 2017.Oppgave 3 (4 poeng)
Ved en videregående skole er det 640 elever. I en undersøkelse ble elevene spurt om når de legger seg kvelden før en skoledag.- 41 av elevene svarte at de legger seg før klokka 23.
- 54 av elevene som legger seg før klokka 23, har et karaktersnitt over fire.
- 31 av elevene som legger seg etter klokka 23, har et karaktersnitt over fire.
Oppgave 4 (6 poeng)
Oppgave 5 (5 poeng)
Et firma bruker i perioder skoleungdommer for å få unna diverse malerjobber. Ungdommene får timelønn etter alder. I tillegg til timelønn må firmaet betale feriepenger og arbeidsgiveravgift. Firmaet har beregnet at disse utgiftene utgjør 25 % av timelønnen. Du skal lage et regneark som vist nedenfor. I de hvite cellene skal firmaet registrere opplysninger. I de blå cellene skal du sette inn formler.- Timelønn og hvor stor prosentandel av lønnen som firmaet må beregne til feriepenger og arbeidsgiveravgift, skal registreres i celle B3, B4 og B5.
- Når alderen registreres, skal regnearket automatisk gi riktig timelønn.
- Totale kostnader for hver ungdom er summen av lønnen til ungdommen og utgiftene til feriepenger og arbeidsgiveravgift.

Oppgave 6 (6 poeng)

Oppgave 7 (5 poeng)
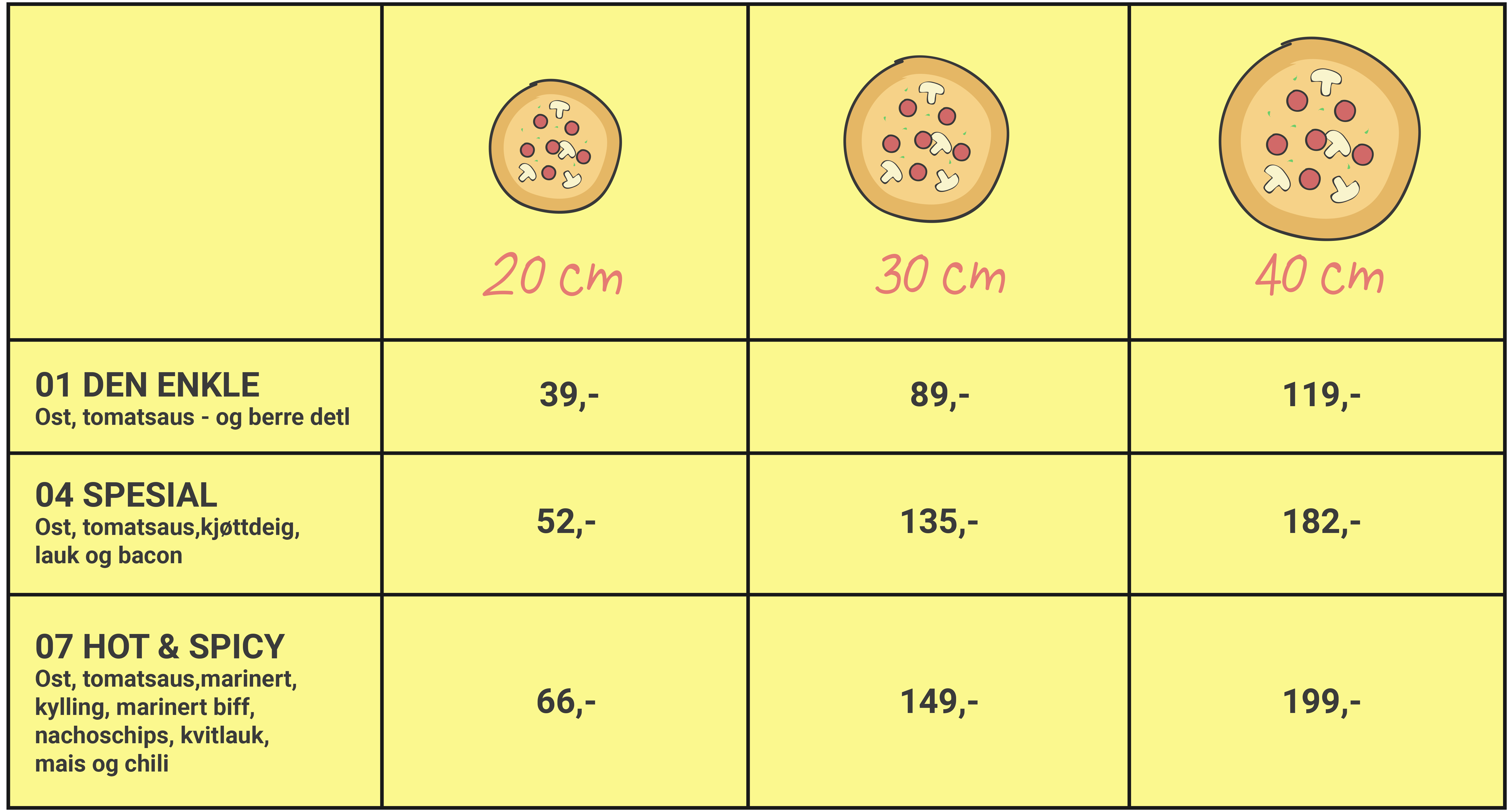
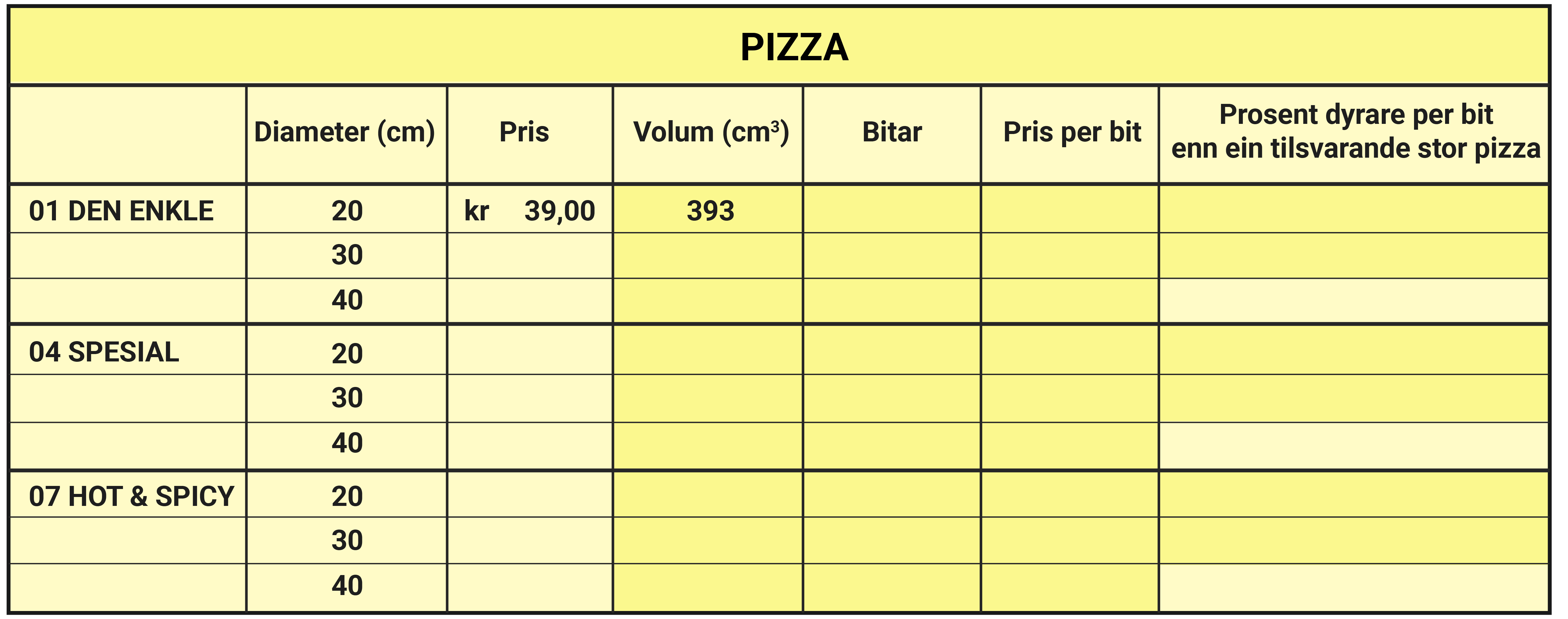
En pizzarestaurant tilbyr pizzaer i tre ulike størrelser.- Den minste pizzaen har en diameter på 20 cm, den mellomstore har en diameter på 30 cm, og den største har en diameter på 40 cm.
- Alle pizzaene er 1,25 cm tykke.
Prøvesmak våre videoer
Mattevideo tilbyr fullstendig dekning av kursene 1P, 1PY, 1T, 2P, S1, R1, S2 og R2 innenfor videregående skole. Under har vi lagt ut noen smakebiter fra disse kursene, så du kan sjekke ut noe av det vi har å by på, før du bestemmer deg for å bli abonnent.1P - Polynomfunksjoner1PY - Prosentregning1T - Funksjonsbegrepet2P - Første gradS1 - LikningssettR1 - Å finn den deriverte ved å bruke derivasjonsreglerS2 - Aritmetiske og geometriske rekkerR2 - Sinusfunksjoner og cosinusfunksjoner

Lær å jobbe smarterepå 5 minutter
Det finnes mange ulike studieteknikker, utfordringen er ofte å finne de som fungerer best for deg. I oversikten under finner du enkelt de beste teknikkene.
Alle våre studietips er laget av vår superelev - med 6 i snitt fra vgs. Ingen av artiklene tar mer enn 5 minutter å lese - slik at du kan starte læringen så fort som mulig.
Hva skjer i hjernen når du lærer?
 Du møter noe nytt for første gang
Du møter noe nytt for første gang Du kobler den nye tingen med kunnskap du har fra før
Du kobler den nye tingen med kunnskap du har fra før Du repeter og styrker sammenhengene
Du repeter og styrker sammenhengene Du bruker kunnskapen
Du bruker kunnskapen

Vanlige utfordringer - og hvordan løse dem


Teknikkene som gjør deg til en superelev
La oss ringe deg, så finner vi en god løsning.




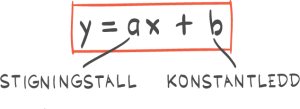























a) Lag verditabell og tegn grafen.
b) Finn stigningstallet og konstantleddet.
c) Hvilken grafisk tolkning har disse tallene?






a) Lag verditabell og tegn grafen.
b) Finn stigningstallet og konstantleddet.
c) Tolk disse tallene grafisk.











Noen venner vil leie en seilbåt i sommerferien. Det koster 18 000 kroner å leie båten. Utgiftene skal deles likt mellom alle som blir med på turen.
a) Hvor mye må hver person betale dersom åtte personer blir med på turen?
Riktig svar!
818000=2250
Riktig svar!
3 er 1 mer enn 2
Riktig svar!
5 - 2(-3) = 5 - (-6) = 5 + 6 = 11
Riktig svar!
2(-3)(-2) = 2(6) = 12
Riktig svar!
Det er motsatt i denne funksjonen: når x øker med 1 øker y med 2.
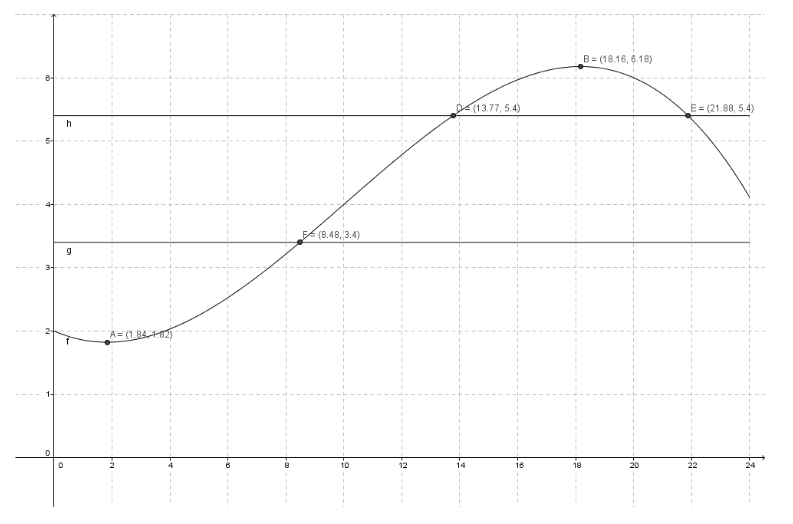
Vi bruker funksjonen f gitt ved
f(x)=−0,002x3+0,06x2−0,2x+2,0≤x≤24
som en modell for vindstyrken f(x)m/s ved en målestasjon x timer etter midnatt 18. mai 2014.
b) Hva var vindstyrken klokken 09⋅45 ifølge modellen?
d) I hvilke tidsrom i løpet av dette døgnet var det lett bris ifølge modelle n?
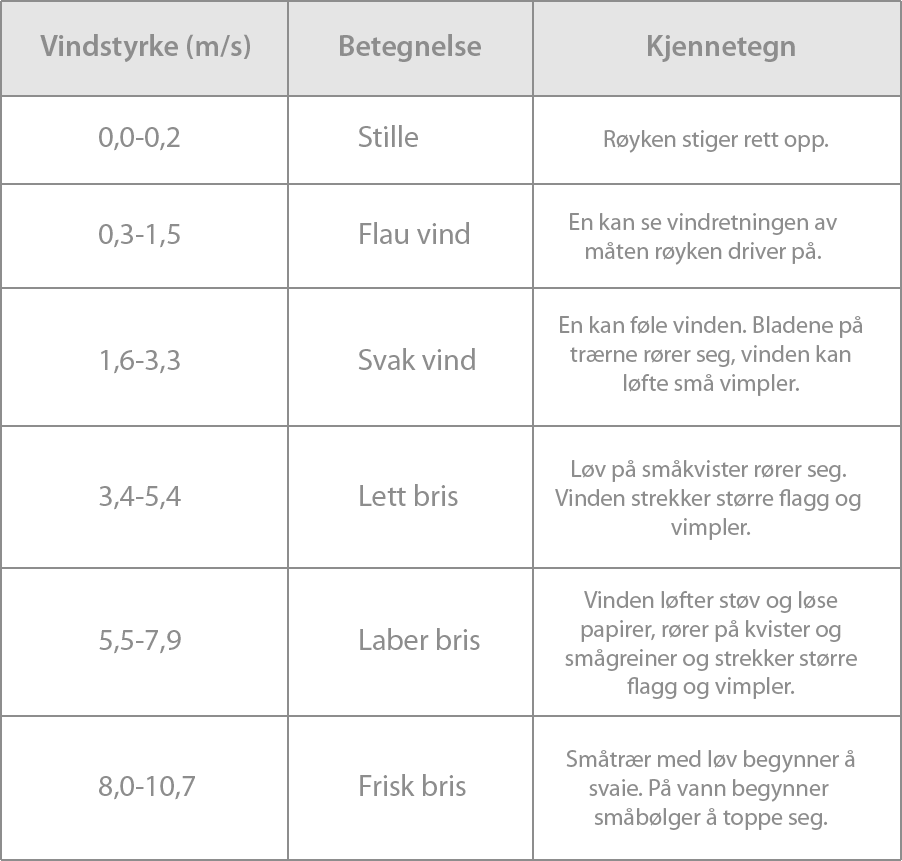
Når klokken er 01:84 etter midnatt er den lavest, og 18:16 er den høyest
Når klokken er 01:50 etter midnatt er den lavest, og 18:10 er den høyest
Når klokken er 8:48 er den høyest, og 13:77 er den lavest
Riktig svar!
Skriv "Ekstremalpunkt[f]" og få punktene A = (1.84, 1.82) og B = (18.16, 6.18). A er bunnpunktet og det betyr at klokken 01:50 (1,84 timer etter midnatt, 1+0,84?601+0,84?60 = 1 time og 50 minutter etter midnatt) var vindstyrken lavest, og den var da 1,82m/s. B er toppunktet og betyr at klokken 18:10 var vindstyrken høyest, da den var 6,18m/s.
Vi bruker funksjonen f gitt ved
f(x)=−0,002x3+0,06x2−0,2x+2,0≤x≤24
som en modell for vindstyrken f(x)m/s ved en målestasjon x timer etter midnatt 18. mai 2014.
Tabellen nedenfor viser sammenhengen mellom vindstyrke og betegnelse.
d) I hvilke tidsrom i løpet av dette døgnet var det lett bris ifølge modelle n?

3,9m/s
3,78m/s
1,92m/s
Riktig svar!
Legg funksjonen inn i GeoGebra og skriv "f(9.75)". Du får da at f(9,75)=3,9f(9,75)=3,9. Vindstyrken var 3,9m/s klokken 09:45.
Vi bruker funksjonen f gitt ved
f(x)=−0,002x3+0,06x2−0,2x+2,0≤x≤24
som en modell for vindstyrken f(x)m/s ved en målestasjon x timer etter midnatt 18. mai 2014.
b) Hva var vindstyrken klokken 09⋅45 ifølge modellen?
c) Når var vindstyrken minst, og når var den størst, ifølge modellen?
d) I hvilke tidsrom i løpet av dette døgnet var det lett bris ifølge modelle n?

Fra 08:29 til 13:46, og fra 21:53 til 00:00
Fra 00:00 til 08:29, og fra 13:46 til 21:53
Fra 01:50 til 18:10
Riktig svar!
Legg inn funksjonene g(x) = 3,4 og h(x) = 5,4 i GeoGebra, og bruk skjæringsverktøyet til å finne ut når f skar med de nye grafene. Du finner da at f skar g ved x = 8,48, og skar h ved x = 13,77 og x = 21,88. Dette betyr at mellom x = 8,48 og x = 13,77 var vindstyrken en "lett bris". Etter x = 13,77 ble vindstyrken høyere, og blir klassifisert som laber bris. Etter x = 21,88 faller vindstyrken under 5,4m/s igjen, og blir lett bris, som varer ut døgnet. Det var lett bris fra 08:29 til 13:46, og fra 21:53 til 00:00 (ut døgnet).
Riktig svar!
Ja, da vil man få forskjellige ledd i funksjonen.
Riktig svar!
Riktig svar!
ledd + ledd = sum og ledd - ledd = differens
Skriv så enkelt som mulig
2x(x−2)−(x−2)(2x+1)
−x+2
−4x2+x−4
−4
Riktig svar!
2x(x−2)−(x−2)(2x+1)
=2x2−4x−(2x2+x−4x−2)
=2x2−4x−2x2−x+4x+2
=−x+2
I 2012 var indeksen for en vare 80. Varen kostet da 2 000 kroner. I 2016 var indeksen for varen 60.
Hvor mye ville varen kostet i 2016 dersom prisen hadde fulgt indeksen?
Riktig svar!
2000 kr tilsvarer en indeks på 80. x tilsvarer en indeks på 60. Dersom det er sammsvar mellom pris og indeks:
6080=x2000
80x=120000
x=1500
I 2016 ville varen kostet 1500 kroner, dersom den følger indeksen.
1,0 g salt inneholder 0,4 g natrium. Helsemyndighetene anbefaler et inntak av natrium på maksimalt 2,4 g per dag.
a) Hvor mange gram salt kan du maksimalt innta i løpet av en dag dersom du skal følge anbefalingen?
100 g pizza inneholder 0,8 g salt. En porsjon pizza er beregnet til 300 g.
b) Hvor mange gram salt inneholder en porsjon pizza?
c) Hvor mange prosent av anbefalt daglig inntak av natrium svarer dette til?
Maksimalt 0.96 g salt hver dag
Maksimalt 6 g salt hver dag
Maksimalt 2.4 g salt hver dag
Riktig svar!
x2.4=10.4
0.4x=2.4
x=0.42.4=6
Man bør ikke spise mere enn 6 gram salt daglig.
1,0 g salt inneholder 0,4 g natrium. Helsemyndighetene anbefaler et inntak av natrium på maksimalt 2,4 g per dag.
a) Hvor mange gram salt kan du maksimalt innta i løpet av en dag dersom du skal følge anbefalingen?
100 g pizza inneholder 0,8 g salt. En porsjon pizza er beregnet til 300 g.
b) Hvor mange gram salt inneholder en porsjon pizza?
c) Hvor mange prosent av anbefalt daglig inntak av natrium svarer dette til?
24 g salt
2.4 g salt
0.8 g salt
Riktig svar!
Dersom 100g inneholder 0,8g vil 300g inneholde tre ganger så mye:
0,8g⋅3=2,4g salt
En porsjon pizza inneholder 2,4 gram salt.
Riktig svar!
Fordi da kan man sette felles faktor utenfor en parentes med alle leddene delt på felles faktor inne i parentesen.
Riktig svar!
Dette er ikke lov fordi man ikke nødvendigvis endrer verdien til den ene siden like mye som den andre.
Løs likningen
2^\left( {2+\frac{x}{2}} \right)=16
12
24
4
Riktig svar!
22+2x=16
22+2x=24
2+2x=4
4+x=8
x=4
Løs likningen
2lgx+8=2−lgx
x=lg3−6
x=−2
x=0,01
Riktig svar!
2lgx+8=2−lgx
2lgx+lgx=2−8
3lgx=−6
lgx=3−6
lgx=−2
10lgx=10−2
x=10−2=0,01
Riktig svar!
Det er ikke noe mulighet til å multiplisere i et kryss i denne situasjonen.
Parklands formel brukes for å beregne hvor mange milliliter væske en pasient med store brannskader skal ha tilført i løpet av de 24 første timene etter en forbrenning.

En pasient veier 63 kg, og 25 % av kroppens overflateareal er forbrent.
a) Hvor mange liter væske skal pasienten ha tilført i løpet av de 24 første timene etter forbrenningen?
En annen pasient veier 85 kg. En lege beregner at pasienten skal ha tilført 10 L væske de første 24 timene etter en forbrenning.
b) Hvor stor prosentandel av kroppens overflateareal er forbrent hos denne pasienten?
Riktig svar!
V=4⋅63⋅25
V=6300mL
6300 mL = 6,3 L

Ei kake har form som ein sylinder med diameter 26,0 cm og høgde 8,0 cm.
a) Bestem volumet av kaka. Oppgi svaret i liter.
Ingrid skal dekkje kaka med marsipan på toppen og på sidene. Ho vil starte med å kjevle ut ein sirkel av marsipan. Denne sirkelen blir kalla marsipanlokket.
I oppskrifta står det at ho må gjere dette for å bestemme kor stort marsipanlokket bør vere:
Mål kor stor diameter kaka har, og kor høg ho er. Legg saman diameteren og to gonger høgda. Legg deretter til 7 cm ekstra. Da har du den totale diameteren til lokket.
b) Bestem arealet av marsipanlokket.
c) Vis at forholdet mellom arealet av marsipanlokket og overflatearealet til kaka er tilnærma lik 1,6.
Riktig svar!
Volumet av et sylinder er grunnflate⋅høyde
Grunnflate=π⋅r=π⋅132=531cm2
V=531cm2⋅8cm=4247cm3
4247cm3≈4,3dm3=4,3L
Eva lager blomsterpotter. Blomsterpottene har form som sylindre. Eva følger denne regelen
når hun lager pottene:
«Summen av omkretsen og høyden skal være 50 cm.»
Eva vil lage en blomsterpotte som er 15 cm høy.
a) Bestem volumet av denne blomsterpotten dersom Eva følger regel en ovenfor.
Funksjonene f og g er gitt ved
f(x)=50−2Πx
g(x)=Πx2(50−2Πx)
b) Forklar hva de to funksjonene uttrykker om sammenhengen mellom blomsterpottenes
radius, høyde og volum.
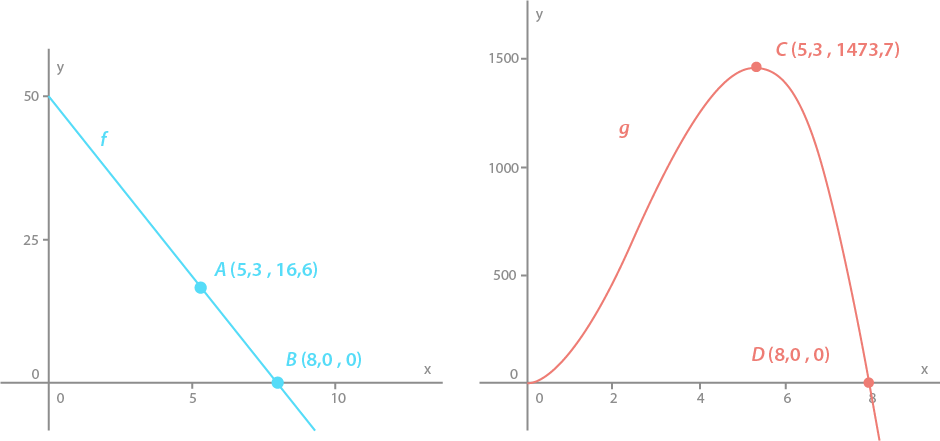
Ovenfor har vi tegnet grafene til funksjonene f og g .
På hver graf har vi markert to punkter.
c) Hva kan du si om blomsterpottene som lages etter regelen ovenfor, ut fra grafene
og de markerte punktene?
262⋅5cm3
1462cm3
165⋅4cm3
Riktig svar!
50cm−15cm=35cm
Dersom blomsterpotten skal være 15m høy, må den ha en omkrets på 35cm.
r=2π35cm=5,57cm
V=πr2h=π⋅(5,57cm)2⋅15cm=1462cm3
Parklands formel brukes for å beregne hvor mange milliliter væske en pasient med store brannskader skal ha tilført i løpet av de 24 første timene etter en forbrenning.

En pasient veier 63 kg, og 25 % av kroppens overflateareal er forbrent.
a) Hvor mange liter væske skal pasienten ha tilført i løpet av de 24 første timene etter forbrenningen?
En annen pasient veier 85 kg. En lege beregner at pasienten skal ha tilført 10 L væske de første 24 timene etter en forbrenning.
b) Hvor stor prosentandel av kroppens overflateareal er forbrent hos denne pasienten?
Riktig svar!
V=4⋅m⋅A
A=4⋅mV
A=34010000=29.4
En formel er gitt ved
s=vo⋅t+21⋅a⋅t2
a) Bestem s når vo=0,t=8oga=10
b) Bestem a når vo=20,t=4ogs=144
Riktig svar!
b)
s=v0t+21at2
(s−v0t)2=at2
a=t22(s−v0t)
a=162(144−20⋅4)
a=8
Riktig svar!
4cm⋅3cm=12cm2
En formel er gitt ved
s=vo⋅t+21⋅a⋅t2
a) Bestem s når vo=0,t=8ogs=10
b) Bestem a når vo=20,t=4oga=144
Riktig svar!
s=v0+21at2
s=0⋅8+21⋅10⋅82
s=0+2640
s=320
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
Riktig svar!
I Norge måler vi temperatur i grader celsius. I USA blir temperaturen målt i grader fahrenheit. I tabellen nedenfor ser du sammenhengen mellom grader celsius og grader fahrenheit.

a) Tegn et koordinatsystem med grader celsius langs x-aksen og grader fahrenheit langs y-aksen. Marker verdiene fra tabellen som punkter i koordinatsystemet, og tegn en rett linje som går igjennom punktene.

Tenk deg at du har en gradstokk som viser grader celsius, og en gradstokk som viser grader fahrenheit.
b) Hvor kaldt må det være ute for at de to gradstokkene skal vise samme verdi?
c) Bestem en formel som viser sammenhengen mellom grader celsius og grader fahrenheit.
d) Bruk formelen du fant i oppgave c) til å vise at 100 grader celsius er det samme som 212 grader fahrenheit.
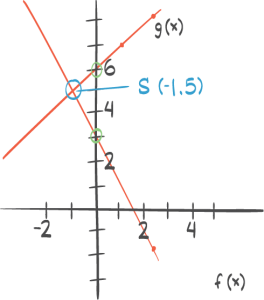
Funksjonene f og g er gitt ved
f(x)=21x
g(x)=−x+3
a) Tegn grafene til f og g i samme koordinatsystem, og bestem skjæringspunktet grafisk.
b) Bestem skjæringspunktet ved regning.
f(x)=g(x)
21x=−x+3
x=−2x+6
3x=6
x=2
f(2)= 1
Skjæringspunkt mellom f og g : (2,1)
Funksjonene f og g er gitt ved
f(x)=21x
g(x)=−x+3
a) Tegn grafene til f og g i samme koordinatsystem, og bestem skjæringspunktet grafisk.
b) Bestem skjæringspunktet ved regning.
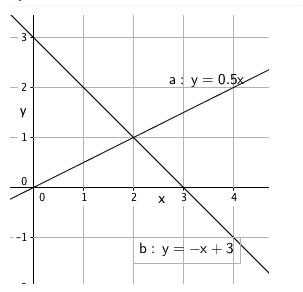
Ved avlesning: skjæringspunkt i (2, 1).
I Norge måler vi temperatur i grader celsius. I USA blir temperaturen målt i grader fahrenheit. I tabellen nedenfor ser du sammenhengen mellom grader celsius og grader fahrenheit.

a) Tegn et koordinatsystem med grader celsius langs x-aksen og grader fahrenheit langs y-aksen. Marker verdiene fra tabellen som punkter i koordinatsystemet, og tegn en rett linje som går igjennom punktene.

Tenk deg at du har en gradstokk som viser grader celsius, og en gradstokk som viser grader fahrenheit.
b) Er antall grader celsius proporsjonalt med antall grader fahrenheit? Begrunn svaret.
c) Hvor kaldt må det være ute for at de to gradstokkene skal vise samme verdi?
d) Bestem en formel som viser sammenhengen mellom grader celsius og grader fahrenheit.
e) Bruk formelen du fant i oppgave c) til å vise at 100 grader celsius er det samme som 212 grader fahrenheit.
I Norge måler vi temperatur i grader celsius. I USA blir temperaturen målt i grader fahrenheit. I tabellen nedenfor ser du sammenhengen mellom grader celsius og grader fahrenheit.

a) Tegn et koordinatsystem med grader celsius langs x-aksen og grader fahrenheit langs y-aksen. Marker verdiene fra tabellen som punkter i koordinatsystemet, og tegn en rett linje som går igjennom punktene.

Tenk deg at du har en gradstokk som viser grader celsius, og en gradstokk som viser grader fahrenheit.
Tenk deg at du har en gradstokk som viser grader celsius, og en gradstokk som viser grader fahrenheit.
b) Er antall grader celsius proporsjonalt med antall grader fahrenheit? Begrunn svaret.
c) Hvor kaldt må det være ute for at de to gradstokkene skal vise samme verdi?
d) Bestem en formel som viser sammenhengen mellom grader celsius og grader fahrenheit.
e) Bruk formelen du fant i oppgave c) til å vise at 100 grader celsius er det samme som 212 grader fahrenheit.
Hvis man ser på figuren, vil man se at grafen krysser der hvor strekene til -40 på x-aksen og y-aksen møtes. Det betyr at celsius og fahrenheit har samme verdi når det er -40 grader ute.
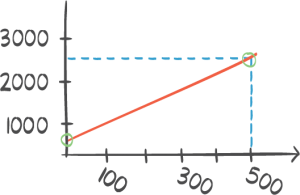
Anders skal leie en bil hos bilfirma A eller bilfirma B. Grafene nedenfor viser hvor mye han må betale til hvert firma dersom han leier bilen én dag og kjører x kilometer.
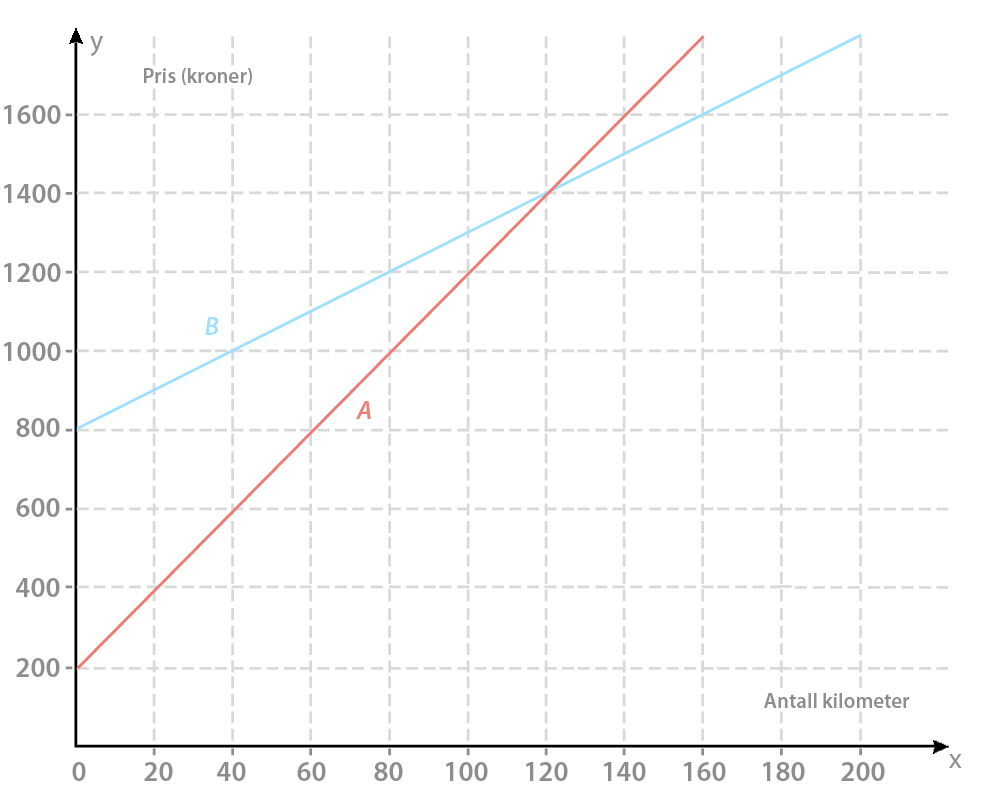
a) Sett opp et funksjonsuttrykk for hver av de to grafene.
b) Hva forteller den grafiske framstillingen om de to pristilbudene?
c) Er antall kilometer han kjører, og prisen han totalt må betale, proporsjonale størrelser? Begrunn svaret ditt.
A:
Grafen begynner på 200 på y- aksen, når x ( antall kilometer er null). Det betyr at b = 200. Når x = 20 er y = 400. På 20 x enheter har y økt med 200. Det betyr at når x øker med en, øker y med 10. Da blir funksjonsuttrykket :
y = 10x + 200
B:
y= 5x + 800
I Norge måler vi temperatur i grader celsius. I USA blir temperaturen målt i grader fahrenheit. I tabellen nedenfor ser du sammenhengen mellom grader celsius og grader fahrenheit.

a) Tegn et koordinatsystem med grader celsius langs x-aksen og grader fahrenheit langs y-aksen. Marker verdiene fra tabellen som punkter i koordinatsystemet, og tegn en rett linje som går igjennom punktene.

Tenk deg at du har en gradstokk som viser grader celsius, og en gradstokk som viser grader fahrenheit.
b) Er antall grader celsius proporsjonalt med antall grader fahrenheit? Begrunn svaret.
c) Hvor kaldt må det være ute for at de to gradstokkene skal vise samme verdi?
d) Bestem en formel som viser sammenhengen mellom grader celsius og grader fahrenheit.
e) Bruk formelen du fant i oppgave d) til å vise at 100 grader celsius er det samme som 212 grader fahrenheit.
\begin{equation} F = 1,8C + 32 \\\ F = 1,8 \cdot 100 + 32 \\\ F = 180 + 32 \\\ F = 212 \\\ \end{equation}
På et treningssenter har de to ulike prisavtaler.
Avtale 1: Du betaler 160 kroner per måned. I tillegg betaler du 20 kroner hver gang du
trener.
Avtale 2: Du betaler 400 kroner per måned. Da kan du trene så mye du vil.
Kari trener på treningssenteret. Hun har valgt avtale 1.
a) I januar trente hun 8 ganger. I februar trente hun 14 ganger.
Hvor mye måtte hun betale for treningen hver av disse to månedene?
b) Tegn en graf som viser sammenhengen mellom antall ganger Kari trener en
måned, og prisen hun må betale denne måneden.
c) Bruk grafen i oppgave b) til å bestemme hvor mye hun må trene for at det skal lønne
seg med avtale 2.
La A være antall ganger du trener en måned. La P være prisen per trening.
d) For hver av avtalene 1 og 2 skal du avgjøre om A og P er
- proporsjonale størrelser
- omvendt proporsjonale størrelser
Lagde en ny funksjon hvor y = 400 i GeoGebra, brukte skjæringsverktøyet og så at grafene skjærte ved x = 12. Hun må altså trene 12 ganger for at avtalene skal være like billig. Derfor må hun trene 13 ganger eller mer for at avtale 2 skal lønne seg.
Vi bruker funksjonen f gitt ved
f(x)=−0,002x3+0,06x2−0,2x+2,0≤x≤24
som en modell for vindstyrken f(x)m/s ved en målestasjon x timer etter midnatt 18. mai 2014.
a) Tegn grafen til f.
c) Når var vindstyrken minst, og når var den størst, ifølge modellen?
Tabellen nedenfor viser sammenhengen mellom vindstyrke og betegnelse.
d) I hvilke tidsrom i løpet av dette døgnet var det lett bris ifølge modelle n?

Funksjonen f er gitt ved
f(x)=x2+2x−3
a) Skriv av verditabellen nedenfor i besvarelsen din, og fyll inn tallene som mangler.

b) Tegn grafen til f for −4≤x≤2
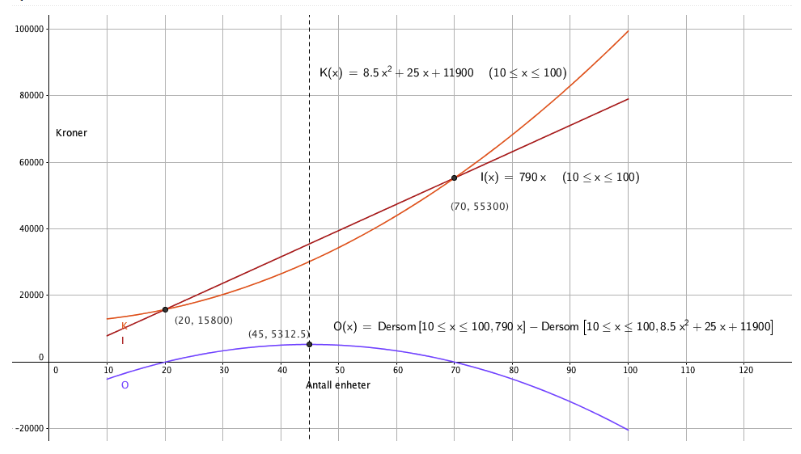
En bedrift produserer og selger en vare. Kostnadene K(x) kroner og inntektene I(x) kroner ved produksjon og salg av x enheter av varen er gitt ved
K(x)=8,5x2+25x+1190010≤x≤100
l(x)=790x10≤x≤100
a) Bruk graftegner til å tegne grafene til funksjonene K og I i samme koordinatsystem.
b) For hvilke verdier av x er inntektene og kostnadene like store?
c) Hvor mange enheter av varen må bedriften produsere og selge for at overskuddet skal bli størst mulig? Hvor stort blir overskuddet da?
Kostnader og inntekter er like store for 20 og 70 enheter, fra figuren i a.
En bedrift produserer og selger en vare. Kostnadene K(x) kroner og inntektene I(x) kroner ved produksjon og salg av x enheter av varen er gitt ved
K(x)=8,5x2+25x+1190010≤x≤100
l(x)=790x10≤x≤100
a) Bruk graftegner til å tegne grafene til funksjonene K og I i samme koordinatsystem.
b) For hvilke verdier av x er inntektene og kostnadene like store?
c) Hvor mange enheter av varen må bedriften produsere og selge for at overskuddet skal bli størst mulig? Hvor stort blir overskuddet da?
Funksjonane L og N er gitt ved L(x)=−0,0025x3+0,089x2−0,67x+6,12 , x∈[0,24] N(x)=−0,00016x3+0,01x2−0,31x+1,15 , x∈[0,24] Funksjonene viser temperaturene L(x) grader celsius ved Lindesnes og N(x) grader celcius ved Nordkapp x timer etter midnatt et døgn i januar 2019.
a) Bruk graftegner til å tegne grafene til L og N.
b) Bestem den momentane vekstfarten til hver av funksjonene når x = 8. Gi en praktisk tolkning av disse svarene.
c) Bestem temperaturforskjellen mellom Lindesnes og Nordkapp klokka 12.00.
d) Når var temperaturforskjellen mellom Lindesnes og Nordkapp størst dette døgnet? Hvor stor var forskjellen da?

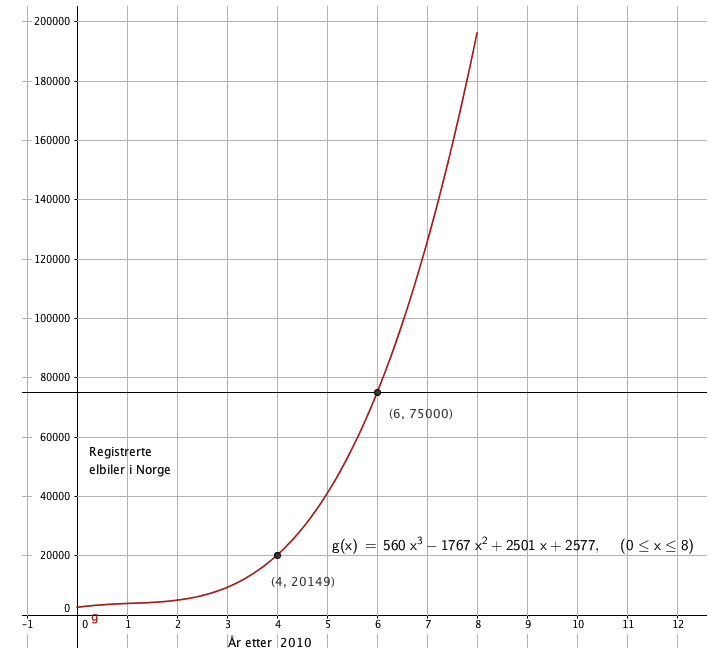
Anta at antall registrerte elbiler i Norge x år etter 2010 tilnærmet er gitt ved
funksjonen g der
g(x)=560x3−1767x2+2501x+2577 0≤x≤8
- a) Bruk graftegner til å tegne grafen til g .
- b) Når vil antall registrerte elbiler passere 75 000 ifølge denne funksjonen?
- c) Bestem g(4). Hva forteller denne verdien om antall elbiler?
g(4) forteller oss at i 2014 var det 20149 registrerte elbiler i Norge.
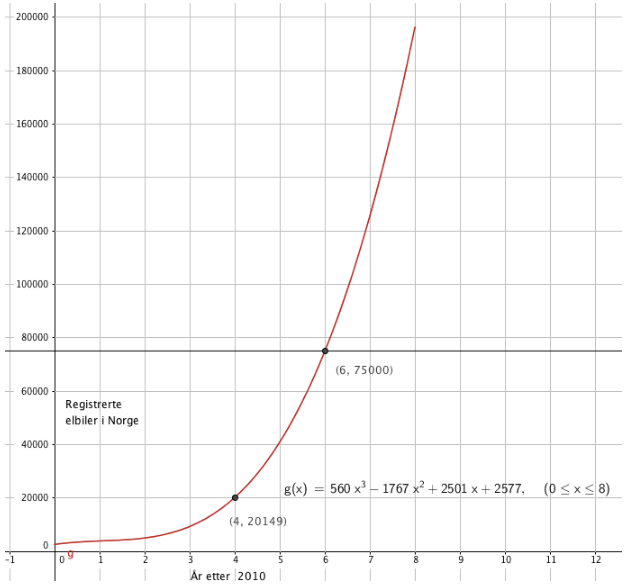

Anta at antall registrerte elbiler i Norge x år etter 2010 tilnærmet er gitt ved
funksjonen g der
g(x)=560x3−1767x2+2501x+2577 0≤x≤8
- a) Bruk graftegner til å tegne grafen til g .
- b) Når vil antall registrerte elbiler passere 75 000 ifølge denne funksjonen?
- c) Bestem g(4). Hva forteller denne verdien om antall elbiler?
Det skjer i 2016, i følge modellen.
En bedrift produserer og selger en vare. Kostnadene K(x) kroner og inntektene I(x) kroner ved produksjon og salg av x enheter av varen er gitt ved
K(x)=8,5x2+25x+1190010≤x≤100
l(x)=790x10≤x≤100
a) Bruk graftegner til å tegne grafene til funksjonene K og I i samme koordinatsystem.
b) For hvilke verdier av x er inntektene og kostnadene like store?
c) Hvor mange enheter av varen må bedriften produsere og selge for at overskuddet skal bli størst mulig? Hvor stort blir overskuddet da?
For at overskuddet skal bli størst mulig må det produseres og selges 45 enheter. Overskuddet er da 5312,50 kroner.
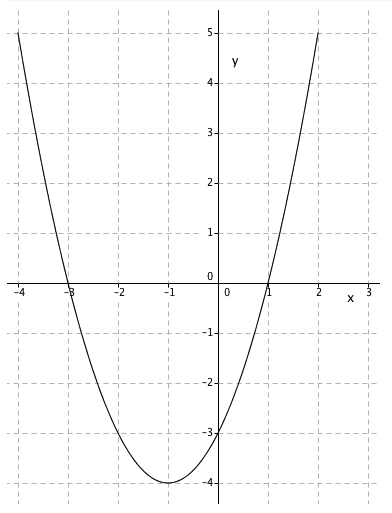
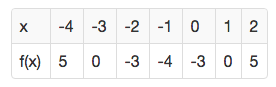
Funksjonen f er gitt ved
f(x)=x2+2x−3
a) Skriv av verditabellen nedenfor i besvarelsen din, og fyll inn tallene som mangler.

b) Tegn grafen til f for −4≤x≤2
Funksjonen f er gitt ved
f(x)=−0,003x3−0,005x2+0,8x,0≤x≤18
a) Tegn grafen til f .
b) Bestem nullpunktene til f. Bestem toppunktet på grafen til f.
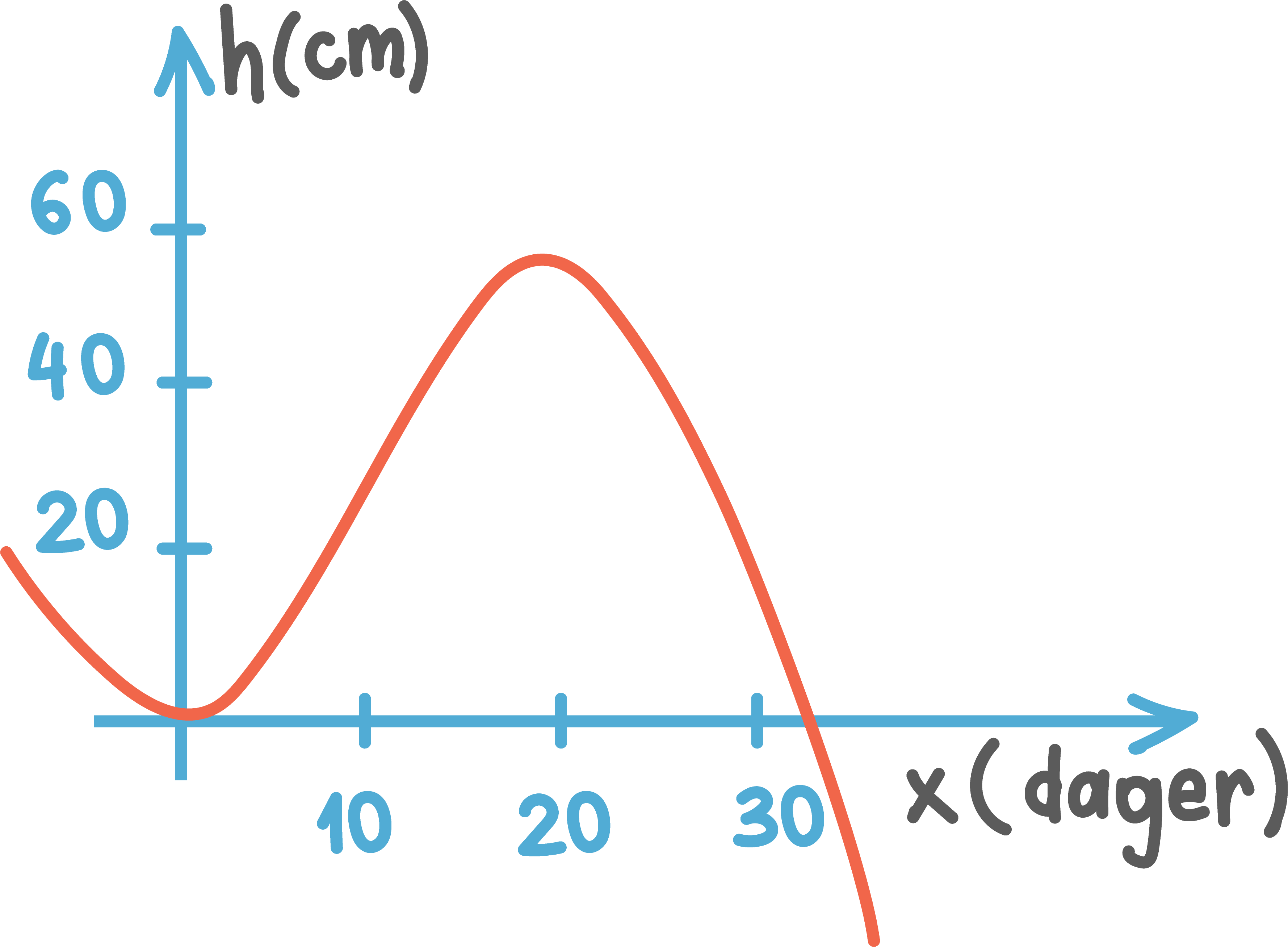
En sommernatt begynte det å snø i en fjellbygd. Når f(x)≥0 viser funksjonen f snødybden f(x) cm i bygda x timer etter midnatt.
c) Hva forteller svarene du fant i oppgave b) om snødybden i fjellbygda?
Snøen begynte å legge seg ved midnatt. Den nådde et maksimum på 4,6 cm. etter ca. ni timer, altså rett før ni på morgenen. Snøen smelter raskt utover ettermiddagen og er borte ca. halv fire.
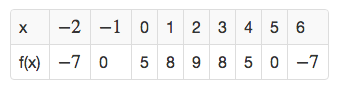
En funksjon f er gitt ved
f(x)=−x2+4x+5a) Skriv av og fyll ut verditabellen nedenfor.

b) Tegn grafen til f .
Funksjonen f er gitt ved
f(x)=−0,003x3−0,005x2+0,8x,0≤x≤18
a) Tegn grafen til f .
b) Bestem nullpunktene til f. Bestem toppunktet på grafen til f.
En sommernatt begynte det å snø i en fjellbygd. Når f(x)≥0 viser funksjonen f snødybden f(x) cm i bygda x timer etter midnatt.
c) Hva forteller svarene du fant i oppgave b) om snødybden i fjellbygda?
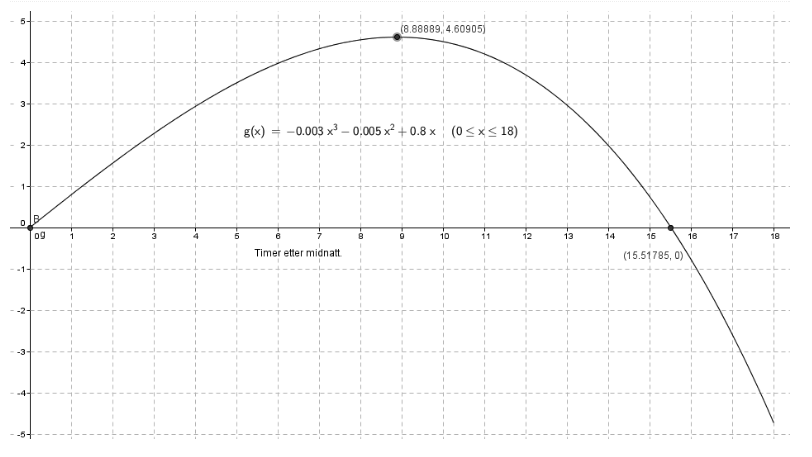
Leser av grafen i a og finner at nullpunkter er (0,0) og (15,52 , 0).
Toppunktet er (8,89, 4,61), fra grafen i a.
Funksjonane L og N er gitt ved L(x)=−0,0025x3+0,089x2−0,67x+6,12 , x∈[0,24] N(x)=−0,00016x3+0,01x2−0,31x+1,15 , x∈[0,24] Funksjonene viser temperaturene L(x) grader celsius ved Lindesnes og N(x) grader celcius ved Nordkapp x timer etter midnatt et døgn i januar 2019.
a) Bruk graftegner til å tegne grafene til L og N.
b) Bestem den momentane vekstfarten til hver av funksjonene når x = 8. Gi en praktisk tolkning av disse svarene.
c) Bestem temperaturforskjellen mellom Lindesnes og Nordkapp klokka 12.00.
d) Når var temperaturforskjellen mellom Lindesnes og Nordkapp størst dette døgnet? Hvor stor var forskjellen da?
Funksjonen f er gitt ved
f(x)=−0,003x3−0,005x2+0,8x,0≤x≤18
a) Tegn grafen til f .
b) Bestem nullpunktene til f. Bestem toppunktet på grafen til f.
En sommernatt begynte det å snø i en fjellbygd. Når f(x)≥0 viser funksjonen f snødybden f(x) cm i bygda x timer etter midnatt.
c) Hva forteller svarene du fant i oppgave b) om snødybden i fjellbygda?

Funksjonane L og N er gitt ved L(x)=−0,0025x3+0,089x2−0,67x+6,12 , x∈[0,24] N(x)=−0,00016x3+0,01x2−0,31x+1,15 , x∈[0,24] Funksjonene viser temperaturene L(x) grader celsius ved Lindesnes og N(x) grader celcius ved Nordkapp x timer etter midnatt et døgn i januar 2019.
a) Bruk graftegner til å tegne grafene til L og N.
b) Bestem den momentane vekstfarten til hver av funksjonene når x = 8. Gi en praktisk tolkning av disse svarene.
c) Bestem temperaturforskjellen mellom Lindesnes og Nordkapp klokka 12.00.
d) Når var temperaturforskjellen mellom Lindesnes og Nordkapp størst dette døgnet? Hvor stor var forskjellen da?
Funksjonene f, g og h er gitt ved
f(x)=−x
g(x)=−x2+x+2
h(x)=21x+1
Nedenfor ser du grafene til seks ulike funksjoner. Hvilken graf er grafen til f, hvilken graf er grafen til g , og hvilken graf er grafen til h ? Begrunn svarene dine.
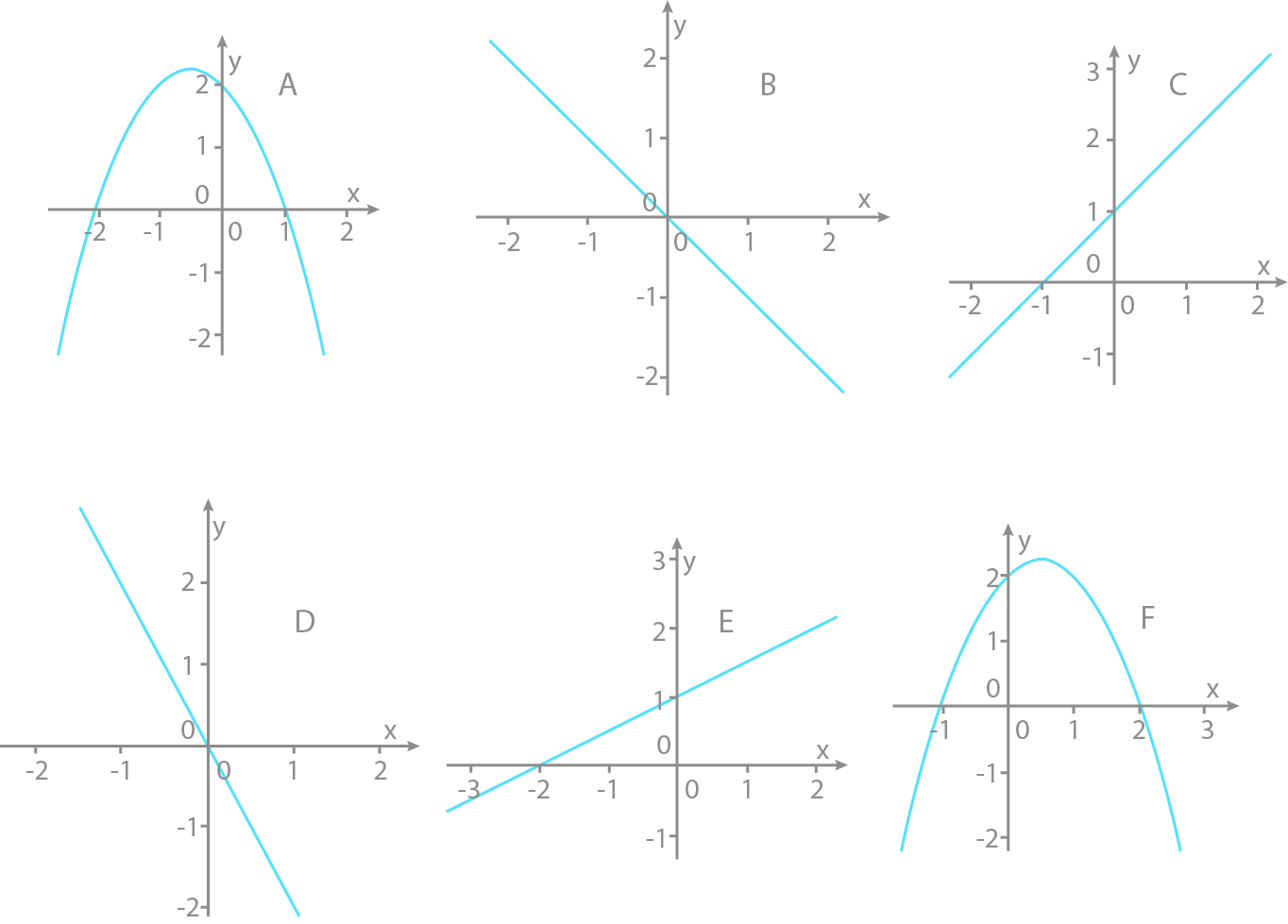
f(x)=−x
Dette er en rett linje uten konstantledd, det betyr at grafen går gjennom origo. Den har stigningstall -1, (en til høyre, en ned) hvilket betyr a B er riktig graf.
g(x)=−x2+x+2
Dette er en parabel eller andregradsfunksjon. Når det står minus foran andregradsleddet betyr det at den vender sin hule side ned. Den skjærer y-aksen i 2. Både graf A og F oppfyller disse kravene. Vi sjekker nullpunktet x = 2 for F: −(22)+2+2=0. Graf F tilhører funksjonen g.
h(x)=21x+1
En rett linje som skjærer y-aksen i en og stiger med en halv. Graf E passer til funksjon h.

Anta at antall registrerte elbiler i Norge x år etter 2010 tilnærmet er gitt ved
funksjonen g der
g(x)=560x3−1767x2+2501x+2577 0≤x≤8
- a) Bruk graftegner til å tegne grafen til g .
- b) Når vil antall registrerte elbiler passere 75 000 ifølge denne funksjonen?
- c) Bestem g(4). Hva forteller denne verdien om antall elbiler?

Funksjonane L og N er gitt ved L(x)=−0,0025x3+0,089x2−0,67x+6,12 , x∈[0,24] N(x)=−0,00016x3+0,01x2−0,31x+1,15 , x∈[0,24] Funksjonene viser temperaturene L(x) grader celsius ved Lindesnes og N(x) grader celcius ved Nordkapp x timer etter midnatt et døgn i januar 2019.
a) Bruk graftegner til å tegne grafene til L og N.
b) Bestem den momentane vekstfarten til hver av funksjonene når x = 8. Gi en praktisk tolkning av disse svarene.
c) Bestem temperaturforskjellen mellom Lindesnes og Nordkapp klokka 12.00.
d) Når var temperaturforskjellen mellom Lindesnes og Nordkapp størst dette døgnet? Hvor stor var forskjellen da?
Funksjonane L og N er gitt ved L(x)=−0,0025x3+0,089x2−0,67x+6,12 , x∈[0,24] N(x)=−0,00016x3+0,01x2−0,31x+1,15 , x∈[0,24] Funksjonene viser temperaturene L(x) grader celsius ved Lindesnes og N(x) grader celcius ved Nordkapp x timer etter midnatt et døgn i januar 2019.
a) Bruk graftegner til å tegne grafene til L og N.
b) Bestem den momentane vekstfarten til hver av funksjonene når x = 8. Gi en praktisk tolkning av disse svarene.
c) Bestem temperaturforskjellen mellom Lindesnes og Nordkapp klokka 12.00.
d) Når var temperaturforskjellen mellom Lindesnes og Nordkapp størst dette døgnet? Hvor stor var forskjellen da?
 Den største temperaturforskjellen er, avrundet, 19,9 grader klokken 22:39 (10 timer og 39 minutter etter midnatt).
Den største temperaturforskjellen er, avrundet, 19,9 grader klokken 22:39 (10 timer og 39 minutter etter midnatt).Funksjonane L og N er gitt ved L(x)=−0,0025x3+0,089x2−0,67x+6,12 , x∈[0,24] N(x)=−0,00016x3+0,01x2−0,31x+1,15 , x∈[0,24] Funksjonene viser temperaturene L(x) grader celsius ved Lindesnes og N(x) grader celcius ved Nordkapp x timer etter midnatt et døgn i januar 2019.
a) Bruk graftegner til å tegne grafene til L og N.
b) Bestem den momentane vekstfarten til hver av funksjonene når x = 8. Gi en praktisk tolkning av disse svarene.
c) Bestem temperaturforskjellen mellom Lindesnes og Nordkapp klokka 12.00.
d) Når var temperaturforskjellen mellom Lindesnes og Nordkapp størst dette døgnet? Hvor stor var forskjellen da?
Funksjonane L og N er gitt ved L(x)=−0,0025x3+0,089x2−0,67x+6,12 , x∈[0,24] N(x)=−0,00016x3+0,01x2−0,31x+1,15 , x∈[0,24] Funksjonene viser temperaturene L(x) grader celsius ved Lindesnes og N(x) grader celcius ved Nordkapp x timer etter midnatt et døgn i januar 2019.
a) Bruk graftegner til å tegne grafene til L og N.
b) Bestem den momentane vekstfarten til hver av funksjonene når x = 8. Gi en praktisk tolkning av disse svarene.
c) Bestem temperaturforskjellen mellom Lindesnes og Nordkapp klokka 12.00.
d) Når var temperaturforskjellen mellom Lindesnes og Nordkapp størst dette døgnet? Hvor stor var forskjellen da?
Ida selger små og store kuleis. En liten kuleis koster 24 kroner og har to iskremkuler. En stor kuleis koster 32 kroner og har tre iskremkuler. En liter iskrem gir i alt 12 iskremkuler.
En dag solgte Ida kuleis for 2 752 kroner. Hun hadde da brukt 20 L iskrem.
Hvor mange store kuleis solgte Ida denne dagen?
Antall små is : x
Antall store is: y
20 liter is gir 12⋅20=240 kuler
2x + 3y = 240
Liten is koster 24 kroner og stor is 32 kroner. Hun solgte for 2752 kroner:
24x + 32y = 2752
Vi kan bruke CAS verktøyet i Geogebra:

Det blir solgt 32 store is, og 72 små is den dagen.
Et trestykke er 35 cm langt. Trestykket skal deles i fire deler.
To deler skal være like lange. Den tredje delen skal være dobbelt så lang som de to like
delene til sammen, og halvparten så lang som den fjerde delen.
Bestem lengden av hver av de fire delene.
De to delene som skal være like lange har lengde x. Vi har da 2x. Den tredje delen er dobbelt så lang som de to like, til sammen, altså er del tre lik 4x. Del fire er dobbelt så lang som del tre, altså 8x.
Vi får da:
2x+4x+8x=35cm 14x=35cm x=2,5cm
De to like stykkene er 2,5 cm hver. Det tredje stykket er 10 cm. Det fjerde stykket er 20 cm.
Et budfirma henter pakker hos forretninger. Pakkene kjøres ut til kunder. Prisen forretningene må betale, avhenger av hvor mye pakkene veier. Se tabellen nedenfor.

a) Du skal lage ett regneark som budfirmaet kan bruke for å registrere bestillinger.

Mathjørnet ønsker å få kjørt ut fire pakker som veier 2 kg, én pakke som veier 8 kg og ti pakker som veier 12 kg.
b) Bruk regnearket du laget i oppgave a), til å vise hvor mye forretningen må betale.
Skomagasinet må betale 1105 kroner for å få kjørt ut fem pakker.
c) Bruk regnearket til å bestemme hvilke typer pakker denne forretningen har bestilt utkjøring for.
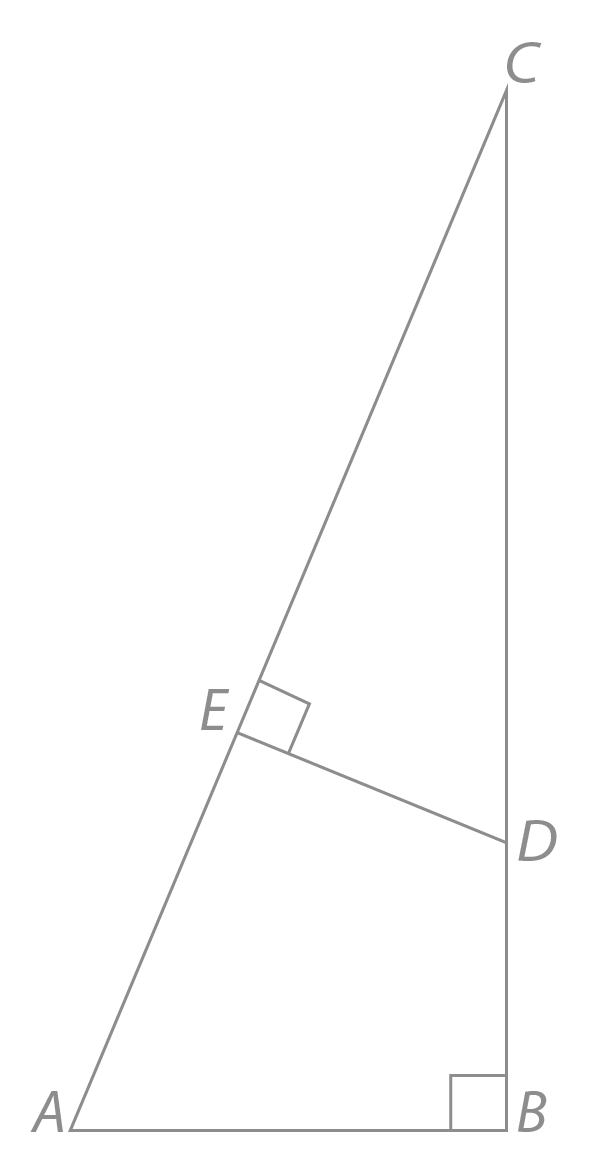
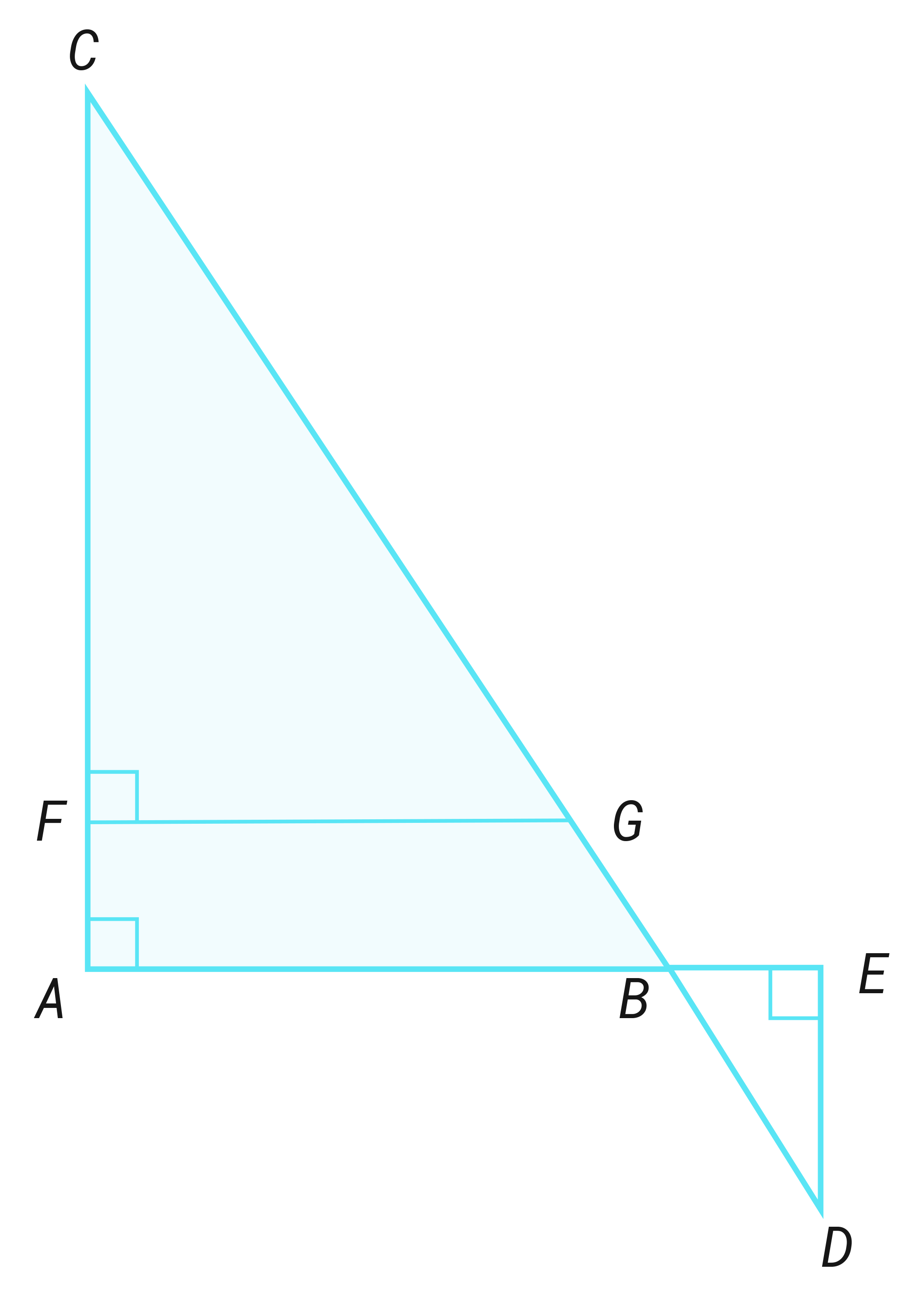
Gitt △ABC og △CED.Se figuren ovenfor.
BC = 36, AC = 39 og CD = 26.
a) Forklar hvorfor △ABC og △CED er formlike.
b) Bestem lengden av CE.
c) Vis at forholdet mellom arealet av △ABC og arealet av △CED er 49.
Trekantene er formlike fordi vinklene er parvis like. Vinkel C er felles i begge. Begge har en rett vinkel. Vinkel A er da like stor som vinkel D i trekanten CED.
Et budfirma henter pakker hos forretninger. Pakkene kjøres ut til kunder. Prisen forretningene må betale, avhenger av hvor mye pakkene veier. Se tabellen nedenfor.

a) Du skal lage ett regneark som budfirmaet kan bruke for å registrere bestillinger.

Mathjørnet ønsker å få kjørt ut fire pakker som veier 2 kg, én pakke som veier 8 kg og ti pakker som veier 12 kg.
b) Bruk regnearket du laget i oppgave a), til å vise hvor mye forretningen må betale.
Skomagasinet må betale 1105 kroner for å få kjørt ut fem pakker.
c) Bruk regnearket til å bestemme hvilke typer pakker denne forretningen har bestilt utkjøring for.
En formel for utregning av bremselengde er gitt ved
s=19,6⋅fv2
der
s = bremselengde (m)
v = fart (m/s)
f = friksjonsfaktor
På tørt sommerføre er friksjonsfaktor f mellom 0,8 og 1,0.
På glatt vinterføre kan f være nede i 0,2.
a) Vis at en fart på 40 km/h tilsvarer en fart på ca. 11,1 m/s.
b) Bestem bremselengden på sommerføre med f = 0,8 når farten er 40 km/h, og når farten er 80 km/h.
Bestem bremselengden på vinterføre med f = 0,2 når farten er 40 km/h, og når farten er 80 km/h.
c) Hvordan endrer bremselengdene i oppgave b) seg når farten dobles? Er bremselengde og fart på glatt vinterføre proporsjonale størrelser?
d) Gjør beregninger og finn en regel for hvor fort du kan kjøre på glatt vinterføre med f = 0,2 for å få samme bremselengde som du har på sommerføre med f=0,8.
Bremselengde sommerføre:
Fart 40 km/h: s=19,6⋅fv2=19,6⋅0.8(11,1m/s)2=7,9m
Fart 80 km/h: s=19,6⋅fv2=19,6⋅0.8(22,2m/s)2=31,5m
Bremselengde vinterføre:
Fart 40 km/h: s=19,6⋅fv2=19,6⋅0.2(11,1m/s)2=31,4m
Fart 80 km/h: s=19,6⋅fv2=19,6⋅0.2(22,2m/s)2=125,7m
En formel for utregning av bremselengde er gitt ved
s=19,6⋅fv2
der
s = bremselengde (m)
v = fart (m/s)
f = friksjonsfaktor
På tørt sommerføre er friksjonsfaktor f mellom 0,8 og 1,0.
På glatt vinterføre kan f være nede i 0,2.
a) Vis at en fart på 40 km/h tilsvarer en fart på ca. 11,1 m/s.
b) Bestem bremselengden på sommerføre med f = 0,8 når farten er 40 km/h, og når farten er 80 km/h.
Bestem bremselengden på vinterføre med f = 0,2 når farten er 40 km/h, og når farten er 80 km/h.
c) Hvordan endrer bremselengdene i oppgave b) seg når farten dobles? Er bremselengde og fart på glatt vinterføre proporsjonale størrelser?
d) Gjør beregninger og finn en regel for hvor fort du kan kjøre på glatt vinterføre med f = 0,2 for å få samme bremselengde som du har på sommerføre med f=0,8.
Fra utregningene i b ser man at farten på vinterstid bør halveres om man ønsker samme bremselengde.
v2=19,5⋅f⋅s
vvinter2vsommer2=19,6s⋅0,219,6s⋅0,8
vvintervsommer=4=2

Gitt △ABC og △CED.Se figuren ovenfor.
BC = 36, AC = 39 og CD = 26.
a) Forklar hvorfor △ABC og △CED er formlike.
b) Bestem lengden av CE.
c) Vis at forholdet mellom arealet av △ABC og arealet av △CED er 49.
Forholdet mellom sidene i trekantene er 2639=23
Forholdet mellom arealene av trekantene blir da:
△CED△ABC=21⋅1⋅121⋅23⋅23=49
Eva lager blomsterpotter. Blomsterpottene har form som sylindre. Eva følger denne regelen
når hun lager pottene:
«Summen av omkretsen og høyden skal være 50 cm.»
Eva vil lage en blomsterpotte som er 15 cm høy.
a) Bestem volumet av denne blomsterpotten dersom Eva følger regel en ovenfor.
Funksjonene f og g er gitt ved
f(x)=50−2Πx
g(x)=Πx2(50−2Πx)
b) Forklar hva de to funksjonene uttrykker om sammenhengen mellom blomsterpottenes
radius, høyde og volum.

Ovenfor har vi tegnet grafene til funksjonene f og g .
På hver graf har vi markert to punkter.
c) Hva kan du si om blomsterpottene som lages etter regelen ovenfor, ut fra grafene
og de markerte punktene?
A og C hører til samme blomsterpotte fordi x = 5,3 i begge. B og D hører til samme blomsterpotte fordi x = 8 i begge.
Vi kan se at ved å sette r=5,3cm vil vi oppnå det høyeste volum mulig om man følger regelen, og da er volumet 1473,7cm3
Vi kan også se at hvis radius er 8cm, vil omkretsen bli 50cm, og h = 50 - 50 = 0cm. Siden h = 0cm ved r = 8 cm , vil volum også bli 0cm3. Man kan altså ikke lage en en blomsterpotte som følger regelen med 8cm eller lengre radius.
Et budfirma henter pakker hos forretninger. Pakkene kjøres ut til kunder. Prisen forretningene må betale, avhenger av hvor mye pakkene veier. Se tabellen nedenfor.

a) Du skal lage ett regneark som budfirmaet kan bruke for å registrere bestillinger.

Mathjørnet ønsker å få kjørt ut fire pakker som veier 2 kg, én pakke som veier 8 kg og ti pakker som veier 12 kg.
b) Bruk regnearket du laget i oppgave a), til å vise hvor mye forretningen må betale.
Skomagasinet må betale 1105 kroner for å få kjørt ut fem pakker.
c) Bruk regnearket til å bestemme hvilke typer pakker denne forretningen har bestilt utkjøring for.
En formel for utregning av bremselengde er gitt ved
s=19,6⋅fv2
der
s = bremselengde (m)
v = fart (m/s)
f = friksjonsfaktor
På tørt sommerføre er friksjonsfaktor f mellom 0,8 og 1,0.
På glatt vinterføre kan f være nede i 0,2.
a) Vis at en fart på 40 km/h tilsvarer en fart på ca. 11,1 m/s.
b) Bestem bremselengden på sommerføre med f = 0,8 når farten er 40 km/h, og når farten er 80 km/h.
Bestem bremselengden på vinterføre med f = 0,2 når farten er 40 km/h, og når farten er 80 km/h.
c) Hvordan endrer bremselengdene i oppgave b) seg når farten dobles? Er bremselengde og fart på glatt vinterføre proporsjonale størrelser?
d) Gjør beregninger og finn en regel for hvor fort du kan kjøre på glatt vinterføre med f = 0,2 for å få samme bremselengde som du har på sommerføre med f=0,8.
40km/h=3600s40000m=11,1m/s
Eva lager blomsterpotter. Blomsterpottene har form som sylindre. Eva følger denne regelen
når hun lager pottene:
«Summen av omkretsen og høyden skal være 50 cm.»
Eva vil lage en blomsterpotte som er 15 cm høy.
a) Bestem volumet av denne blomsterpotten dersom Eva følger regel en ovenfor.
Funksjonene f og g er gitt ved
f(x)=50−2Πx
g(x)=Πx2(50−2Πx)
b) Forklar hva de to funksjonene uttrykker om sammenhengen mellom blomsterpottenes
radius, høyde og volum.

Ovenfor har vi tegnet grafene til funksjonene f og g .
På hver graf har vi markert to punkter.
c) Hva kan du si om blomsterpottene som lages etter regelen ovenfor, ut fra grafene
og de markerte punktene?
f(x) er en funksjon for høyden av blomsterpotten hvor x er radius av sylinderen. 50 representerer det som skal være summen av
høyde og omkrets, og 2πx er omkretsen av sirkelen i snittet av sylinderen.
g(x) er en funksjon som viser volum av blomsterpotten hvor x igjen er radius. Formelen for volum av en sylinder er 2πr2h, men siden vi vet at r=x og h=(50−2πx) kan vi se at funksjonen er lik formelen for volum av sylinder.
I Norge måler vi temperatur i grader celsius. I USA blir temperaturen målt i grader fahrenheit. I tabellen nedenfor ser du sammenhengen mellom grader celsius og grader fahrenheit.

a) Tegn et koordinatsystem med grader celsius langs x-aksen og grader fahrenheit langs y-aksen. Marker verdiene fra tabellen som punkter i koordinatsystemet, og tegn en rett linje som går igjennom punktene.

Tenk deg at du har en gradstokk som viser grader celsius, og en gradstokk som viser grader fahrenheit.
b) Er antall grader celsius proporsjonalt med antall grader fahrenheit? Begrunn svaret.
c) Hvor kaldt må det være ute for at de to gradstokkene skal vise samme verdi?
d) Bestem en formel som viser sammenhengen mellom grader celsius og grader fahrenheit.
e) Bruk formelen du fant i oppgave c) til å vise at 100 grader celsius er det samme som 212 grader fahrenheit.
Bruker det vi vet om lineære funksjoner til å finne konstantene a og b i y = ax + b
b er hvor grafen skjærer y-aksen, altså i (0,32), b er alstå 32.
a er stigningstallet til linjen, hvor vi kan bruke to punktet vi vet.
a=ΔxΔy=1018=1,8
Siden y er fahrenheit og x er celsius, skrive vi: F=1,8⋅C+32
En formel for utregning av bremselengde er gitt ved
s=19,6⋅fv2
der
s = bremselengde (m)
v = fart (m/s)
f = friksjonsfaktor
På tørt sommerføre er friksjonsfaktor f mellom 0,8 og 1,0.
På glatt vinterføre kan f være nede i 0,2.
a) Vis at en fart på 40 km/h tilsvarer en fart på ca. 11,1 m/s.
b) Bestem bremselengden på sommerføre med f = 0,8 når farten er 40 km/h, og når farten er 80 km/h.
Bestem bremselengden på vinterføre med f = 0,2 når farten er 40 km/h, og når farten er 80 km/h.
c) Hvordan endrer bremselengdene i oppgave b) seg når farten dobles? Er bremselengde og fart på glatt vinterføre proporsjonale størrelser?
d) Gjør beregninger og finn en regel for hvor fort du kan kjøre på glatt vinterføre med f = 0,2 for å få samme bremselengde som du har på sommerføre med f=0,8.
Når farten dobles blir bremselengden tilnærmet firedoblet. Dette gjelder både sommer og vinter.
7,931,5≈31,4125,7≈4
Bremselengde og fart er ikke proporsjonale størrelser. Om de hadde vært det skulle den ene doble seg når den andre dobler seg.






























Flott opplegg og undervisning😊
Tusen takk!
Gjorde unna R2 som privatist på et halvt år!! Mattevideo har gjort det mye lettere å fordøye et så tungt pensum på så kort tid. Tusen takk for hjelpa!!😊
Bra undervisning!
Jeg er fornøyd med videone deres det har hjulpet meg til å bestå matten i både Vgs og Uni . Så takk😊
Meget bra!
Tusen takk. Veldig flink lærer. Gode forklaringer.
Helt topp :D
Bra side.
Kjempebra!😊
Bra side. Veldig gode forklaringer😊
Tror dette kommer til å redde meg på noen prøver fremover. Takk! :D
takk for hjelpen
Takk for læreren av denne siden. Det er utrolig en bra side, fikk meg mye. Tusen hjertelig takk
Kan trygt anbefale Arne Hovland! Beste læreren jeg har hatt i løpet av drøyt 20 år med utdanning.
takk for denne siden :D min 1T mattelærer snakker så monotont og gjør matte så kjedelig at interessen svinner vekk og jeg sovner etter 5 minutter.